Lean과 최신 AI(ChatGPT-5, Claude 4.5, Codex)를 활용해 Rust 알고리즘의 정확성을 수학적으로 검증하는 방법을 소개합니다. 1부에서는 규칙 1~5를 통해 환경 구축, 개념 정의, Lean-풍 리팩터링, 그리고 AI 주도 워크플로를 다룹니다.
읽는 데 18분
1일 전
Enter 키를 누르거나 이미지를 클릭해 전체 크기로 보기

정리를 증명하는 AI. 출처: https://openai.com/dall-e-2/
내 라이브러리 패키지 range-set-blaze에는 internal_add라는 핵심 함수가 있다. 이 함수는 정수 구간(range)을 크레이트의 자료구조에 삽입한다. 물론 테스트도 하지만, 테스트는 버그를 놓칠 수 있다. 이상적으로는 수학적 확실성을 갖고 싶다.
더욱이 지금은 내가 손으로 코드를 작성했지만, 앞으로 AI가 우리의 코드를 더 많이 생성하게 될수록, 그 코드가 정확함을 증명(prove)하는 능력은 점점 더 중요해질 것이다.
추신(Aside): Rust 같은 현대 언어 — 그리고 어느 정도는 스마트 포인터와 소유권 관례를 갖춘 C++ — 는 이미 강력한 보장을 제공한다: null 역참조 없음, use-after-free 없음. 하지만 그와 같은 확실성을 알고리즘 자체로까지 확장할 수 있다면? 바로 그 지점에서 Lean 같은 증명 시스템이 등장한다.
2년 전, 정확성 확실성을 얻기 위해 Divyanshu Ranjan과 나는 internal_add의 알고리즘을 Dafny 언어로 이식했다. 그리고 많은 작업 끝에 그 Dafny 버전을 형식적으로 검증했다(기사).
올해는 ChatGPT-5 — Claude Sonnet 4.5와 Codex를 함께 활용해 — 로 해당 알고리즘을 Lean으로 이식하고 검증했다. 그 결과는 4,700줄이 넘는 Lean 증명으로, 거의 증명 작업이나 Lean 경험이 없는 상태에서 만들어졌다.
그렇다고 해서 과정이 쉬웠다는 뜻은 아니다. 알고리즘을 완전히 새로운 언어(러스트 → Lean)로 번역해야 했고, 이 과정에서 세부사항이 빠지거나 오류가 들어갈 수 있었다. 전체 증명 과정은 파트타임으로 약 3주, 수백 번의 왕복 프롬프트, 그리고 대략 50달러의 AI 크레딧이 들었다. 흔히 하는 말처럼, 이것은 “춤추는 돼지”와 같다. 경이로운 점은 춤을 잘 추는지가 아니라, 춤을 춘다는 사실 그 자체다.
Lean을 선택한 이유는 가장 활발한 현대 증명 보조기 중 하나이며, 생태계가 커지고 자동화가 강력하기 때문이다. Lean의 추진력 대부분은 소프트웨어 검증이 아니라 수학에서 온다. 필즈상 수상자인 Terence Tao는 자신의 연구 논문을 Lean으로 형식화했고, 자신의 해석학 I 교재에 대한 Lean 동반서를 썼으며, 형식화 과정에서 출판된 증명 속 작은 오류를 발견하기도 했다. Lean은 이제 수학적 검증에서 선도적 위치에 있으며, 나는 곧 소프트웨어 검증에서도 그럴 것이라고 믿는다.
이번 검증을 진행하면서, Lean과 AI로 — 러스트나 다른 언어로 작성된 — 알고리즘을 검증하는 데 도움이 되는 아홉 가지 규칙을 배웠다. 또한 이 규칙들은 최신 도구로 검증이 얼마나 쉬운지/어려운지 가늠하는 데도 흥미로울 것이다. 결론은 곧 게시될 파트 2에서 다룰 예정이며, 놀라웠던 점과 배운 교훈도 함께 논의한다.
규칙은 다음과 같다:
파트 2에서 다룰 내용:
추신(Aside): 애매모호함을 피하기 위해 “규칙”이라 부르지만, 물론 그저 제안들일 뿐이다.
큰 그림은 그렇다. 그런데 정작 관심 대상인 알고리즘은 무엇을 할까?
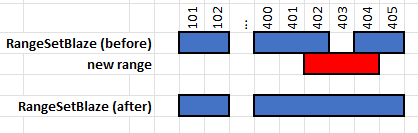
internal_add 함수는 정렬되어 있고 서로 겹치지 않는 정수 구간의 기존 목록에 새로운 정수 구간을 효율적으로 삽입하려고 한다. 예컨대 [101..=102, 400..=402, 404..=405]에 402..=404를 더하면, 결과는 [101..=102, 400..=405]가 되어야 한다.
출처: 이 글의 모든 이미지(별도 표기 없는 한)는 필자 제작.
소개는 이쯤에서 마치고, 과연 시작할 가치가 있는지를 먼저 물어보자.
알고리즘을 형식적으로 증명하기 전에, 그 대가가 노력을 정당화하는지 물어보라. 설령 정당화되더라도, Lean이 그 일에 맞는 도구인지 결정하라.
Lean을 쓰려면 알고리즘을 그 안으로 이식해야 한다 — 이 과정에서 세부가 빠지거나 새 오류가 들어갈 수 있다. 이런 위험을 고려하면, Lean으로 알고리즘을 검증해야 할까? 경우에 따라 다르다.
internal_add 알고리즘은 사람들이 신뢰하길 바라는 자료구조의 기초이기에, 검증하려는 동기가 더 커진다.cargo-fuzz)과 성질 기반 테스트(예: QuickCheck)면 충분할 수도 있다. 이 방법들은 수학적 확실성을 주지는 못하지만, 영리하고 유용하며 사용이 쉽다. (range-set-blaze 크레이트는 이미 QuickCheck를 사용한다. 자세한 내용은 이전 글의 규칙 9.5 참고.)internal_add의 경우, 사양이 어떤 구현보다 훨씬 단순했다. (이는 파트 2의 규칙 6에서 직접 판단해볼 수 있다.)그래도 Lean으로 알고리즘을 포팅하고 검증하겠다면, 좋은 소식: Lean을 제대로 배울 필요는 없다.
놀랍게도, 전통적 의미에서 Lean을 배울 필요가 없다. 교과서도, 전술(tactic) 마스터도 필요 없다. 필요한 것은 작동하는 환경이다:
RangeSetBlaze로 쓴다. 원하는 이름을 사용하라. 커맨드 라인에서:mkdir range-set-blaze-lean
cd range-set-blaze-lean
lake init RangeSetBlaze
Lake(Lean의 Make 또는 Cargo라고 생각하라)가 다음을 만든다:
range-set-blaze-lean/
├── lakefile.toml
├── lake-manifest.json
├── lean-toolchain
├── README.md
├── RangeSetBlaze.lean
├── Main.lean
└── RangeSetBlaze/
└── Basic.lean
프로젝트를 테스트하자:
lake exe rangesetblaze
출력:
Hello, world!
추신(Aside): 아래 지침을 따라 직접 Mathlib을 추가해도 되고, VS Code의 코딩 에이전트에게 이 지시를 그대로 전달해도 된다.
프로젝트에 Mathlib을 추가하려면 lakefile.toml의 끝에 다음을 넣는다:
[[require]]
name = "mathlib4"
git = "https://github.com/leanprover-community/mathlib4"
그리고 VS Code 터미널에서 실행:
lake update
lake exe cache get
Mathlib을 가져오고, 미리 컴파일된 버전을 내려받아 전체를 처음부터 컴파일하지 않아도 된다.
이제 RangeSetBlaze/Basic.lean에 다음을 추가:
import Mathlib.Data.Int.Basic
VS Code 터미널에서 테스트:
lake build # 프로젝트의 모든 Lean 파일을 컴파일
바이브 검증(Vibe Validation)을 할 때는 Git을 반드시 익혀라. 일이 꼬여서 현재 상태를 잃게 된다면 후회할 순간마다 커밋하라.
이제 Lean 준비 완료. Lean 문법을 조금 배우고 싶다면, Dan Abramov의 A Lean Syntax Primer를 추천한다.
다음은 AI에게 Lean 코드를 작성하게 하는 방법이다. 당신의 역할은 알고리즘을 명확히 설명하고, AI의 출력이 의도와 맞는지 확인하며, 엉뚱한 것을 증명하려 들면 제동을 거는 일이다. 페어 프로그래밍이라고 생각하라: 도메인 전문성은 당신이, Lean은 AI가 가져온다.
이번 프로젝트에서 여러 AI 도구를 시도했다. 브라우저의 ChatGPT-5($20/월)로 시작해, GitHub Copilot의 초기 Claude 모델(현재는 “프리미엄 요청” 300회당 $10)로 넘어갔다. 그다음 OpenAI의 Codex를 VS Code 확장으로 사용했고, 마지막으로 Claude Sonnet 4.5였다.
단계가 바뀔수록 업그레이드였다: Codex는 오래된 Claude들보다 나았고, Claude 4.5는 Codex를 이겼다. 이들 모두는 Lean이 Python이나 JavaScript에 비해 틈새 언어임에도 놀랄 만큼 Lean에 능숙했다. 오늘 따라 하려면, 접근 가능한 최신·최고 모델을 그냥 쓰라. 이름은 바뀌어도 워크플로는 바뀌지 않는다.
하지만 함정이 있었다: 할당량(쿼터). Copilot과 Codex 코딩 에이전트는 결국 사용 한도에 걸렸다. 계속 진행하고 — Claude Sonnet 4.5에 접근하기 위해 — GitHub Copilot 구독에 $10, 프리미엄 요청 추가에 $12(약 360회 호출)를 썼다. 반면 브라우저의 ChatGPT-5는 월간 쿼터가 없다. 짧은 버스트는 스로틀링하지만, 1,000줄 이상의 코드가 있는 프롬프트도 기꺼이 받아들인다.
이 작가의 업데이트를 받으려면 Medium에 무료로 가입하세요.
나에게 맞는 승리 조합은 ChatGPT-5가 점진적 단계를 계획하고, 그 지시를 VS Code 안에서 전체 에이전트 모드로 실행 중인 Claude나 Codex에 한 번에 하나씩 먹이는 방식이었다.
추신(Aside): 에이전트 모드는 마법 같다. AI가 Lean 코드를 수정하고, 컴파일하고, 모든 증명이 통과할 때까지(Lean은 만족스러운 녹색 체크로 표시) 계속 재시도한다. 하지만 에이전트를 너무 오래 돌리고 싶지는 않을 때도 있다. 쿼터를 태워버리거나, 증명 불가능한 목표에 갇힐 수 있다. 한 번에 한 입 크기의 목표를 주어, 실행마다 꾸준하고 검증 가능한 진전을 얻는 편이 낫다.
실전에서는: ChatGPT-5는 전략가, Claude나 Codex는 실행자다. 이 조합은 나를 지치게 하거나 쿼터를 너무 빨리 소모하지 않고도 수천 줄의 Lean 증명을 밀어붙였다.
추신(Aside): 나는 이 프로젝트를 두 번 돌렸다 — 한 번은 가능성을 확인하기 위해, 또 한 번은 이 아홉 가지 규칙을 처음부터 검증하기 위해서다.
이제 프로젝트 설정과 워크플로가 갖춰졌으니, 실제 형식화(formalization)를 시작할 차례다. 알고리즘을 구성하는 기본 타입과 관계를 정의하는 것부터 시작한다 — 이후의 모든 증명이 기대게 될 수학적 골격이다.
Lean에서의 첫 작업은 증명의 토대가 될 수학적 기초를 까는 일이다. 목표는 아직 아무것도 증명하는 것이 아니라, 내 경우엔 구간, 집합, 리스트처럼 알고리즘이 조작할 기본 구조를 기술하는 것이다.
다음은 내 AI 코딩 에이전트 Claude Sonnet 4.5에 준 프롬프트다:
I'm working in Lean 4, in the project created by lake init RangeSetBlaze.
Please edit the file RangeSetBlaze/Basic.lean to add the core data structures
for a port of the Rust library RangeSetBlaze.
Here's what I need:
• Define a type that represents an inclusive range of integers, with fields lo and hi.
• Our convention: a range is empty if hi < lo. Use this convention so that
proofs are easier later.
• Define a way to view a range as a set of integers. If the range is empty,
the set should be empty. Use mathlib functions for intervals and sets
wherever possible.
• Add a lemma proving that this set view really is empty when hi < lo.
• Define a predicate that says when one range comes strictly before another
with at least a one-integer gap. This is called disjoint. Use the
symbol ≺ (precedes). This is the opposite of touching or overlapping.
• Define a type for lists of non-empty ranges that are sorted and disjoint.
• Provide a way to convert such a list into a single set that is the union
of all its ranges.
• Please make the definitions efficient to evaluate and rely on mathlib as
much as practical.
Then, in Main.lean, add a few runnable examples:
• Create a couple of non-empty ranges and one empty range.
• Show, with small proofs, that the empty range is indeed empty, and that a
short list of ranges is sorted and disjoint. Create another example of a
list that is not.
• In main, print out those ranges and a short message so I can see something run.
• Keep all the core logic in Basic.lean, since lake init already gave me
that file.
Claude는 몇 분 동안 실행되었다. (이 첫 결과를 GitHub에 커밋했으니 살펴볼 수 있다.)
이제 다시 lake exe rangesetblaze를 실행하면, 생성된 테스트의 출력이 보인다:
RangeSetBlaze - Lean 4 Port Examples
=====================================
Non-empty range 1: { lo := 1, hi := 5 }
Non-empty range 2: { lo := 10, hi := 15 }
Empty range (hi < lo): { lo := 10, hi := 5 }
Range1 is empty: false
Range2 is empty: false
EmptyRange is empty: true
Range1 disjoint from Range2: true
Adjacent ranges are disjoint: false
Overlapping ranges are disjoint: false
Good ranges (sorted & disjoint): [{ lo := 1, hi := 3 }, { lo := 5, hi := 7 }, { lo := 10, hi := 12 }]
All non-empty: true
Sorted and disjoint: true
Bad ranges (overlapping): [{ lo := 1, hi := 5 }, { lo := 4, hi := 8 }]
All non-empty: true
Sorted and disjoint: false
Hello, world!
코드가 컴파일되면, VS Code의 “Problems” 패널을 0으로 만드는 작업을 했다. 도움이 된 다섯 가지 팁:
Basic.lean 같은 파일을 열고, 녹색 체크 표시나 Lean InfoView 패널의 메시지를 보라. 그곳에 오류가 보이면, 파일은 아직 검증되지 않은 것이다.(InfoView 패널 안내)IMPLEMENTATION_NOTES.md라는 추가 파일을 만들었는데 필요 없었고, Markdown 린터가 경고해서 그냥 삭제했다.이 단계에서 알고리즘의 수학적 골격이 정의되고 테스트됐다. 이제 Lean의 관용구로 다시 빚어보자 — 같은 개념을, 그러나 “Lean 방식”으로 재구성한다.
이 시점에서 정의는 동작했지만, 실제로 사용하려 하자 막혔다. 진전을 위해 브라우저의 ChatGPT-5에 코드를 Lean의 관례를 따르도록, 그리고 Mathlib의 기존 보조정리와 자동화와 잘 어울리도록 다시 써달라고 요청했다.
먼저 브라우저 기반 ChatGPT-5에 이렇게 지시했다:
Given these instructions:
<PASTED INSTRUCTIONS FROM ABOVE>
GitHub Copilot/Claude Sonnet 4.5 produced this Basic.lean file:
```lean
<PASTED Basic.lean FILE>
Can you review this and suggest instructions for Claude
that will get it using Mathlib and idiomatic Lean more?
이후 ChatGPT-5가 Claude용 프롬프트를 만들어줬고, 그 프롬프트를 Claude에 넣어 Lean 코드를 생성했다. 그런 다음 다시 ChatGPT-5에게 결과 리뷰와 프롬프트 개선을 요청했다. 이 루프를 몇 차례 반복하고, 중간에 내 아이디어 몇 가지를 더해, 마침내 Lean 문법이 깔끔하고 우리가 목표로 하는 수학을 보여주는 `Basic.lean`에 도달했다. [전체 파일은 GitHub](https://github.com/CarlKCarlK/range-set-blaze-lean/blob/a2a7551/RangeSetBlaze/Basic.lean)에서 볼 수 있다.
몇 가지 스니펫을 보자 — 모든 디테일을 마스터하려는 게 아니라, 코드가 수학에 어떻게 깔끔히 대응되는지를 보기 위해서다.
`Basic.lean`의 첫 줄들은 구간, 집합, 리스트 추론을 위한 Mathlib 일부를 임포트한다:
import Mathlib.Data.Int.Interval
import Mathlib.Data.Set.Lattice
import Mathlib.Data.List.Pairwise
여기서 Claude는 포함적 정수 구간을 위한 구조체를 정의한다. 이 구조체는 출력 가능하며, 필드가 같으면 두 구간은 같다(구조체 동등성):
/
structure IntRange where
lo : Int
hi : Int
deriving Repr, DecidableEq
`namespace`를 사용해 `IntRange` 구조체에 메서드를 정의한다. Lean에서 `Prop`(proposition)은 참/거짓을 증명할 대상으로, 계산이 아니라 추론에 쓰인다. 여기서는 두 가지 단순한 명제를 정의한다: `hi < lo`이면 구간은 “비어 있음(empty)”, `lo ≤ hi`이면 “비어 있지 않음(nonempty)”.
namespace IntRange /
def empty (r : IntRange) : Prop := r.hi < r.lo
/
def nonempty (r : IntRange) : Prop := r.lo ≤ r.hi
이제 `IntRange`를 Mathlib의 구간/집합 체계에 연결한다. 먼저 구간이 “비어 있지 않음”과 “비어 있음이 아님”이 논리적으로 동치임을 보이고, `@[simp]`로 표시해 Lean이 증명 중 자동으로 활용할 수 있게 한다:
/
@[simp]
theorem nonempty_iff_not_empty (r : IntRange) : r.nonempty ↔ ¬ r.empty := by
simp [nonempty, empty, not_lt]
다음으로 `IntRange`를 수학적 집합으로 바라보는 방식을 정의한다 — 구체적으로, `lo`와 `hi` 사이(포함)의 모든 정수들의 집합:
/
def toSet (r : IntRange) : Set Int := Set.Icc r.lo r.hi
Mathlib의 `Set.Icc`(닫힘–닫힘 구간)는 정수 구간에 대한 표준 정리들을 제공한다. 이를 바탕으로, Claude는 다음 **보조정리(lemma)** — 우리 코드 안의 형식적으로 증명된 명제 — 를 만들었다. 이는 구간의 집합 뷰가 정확히 `hi < lo`일 때 비어 있음을 말한다:
/
@[simp]
lemma toSet_eq_empty_iff (r : IntRange) :
r.toSet = (∅ : Set Int) ↔ r.hi < r.lo := by
simp [toSet, Set.Icc_eq_empty_iff, not_le]
> 추신(Aside): Lean에서 theorem과 lemma는 같은 종류의 객체 — 둘 다 증명된 명제다. 관례적으로 더 작은 보조 결과를 lemma, 주요 결론을 theorem이라 부를 뿐이며, 기술적 차이는 없다.
>
> 또 하나: Lean은 표준 코딩 스타일(짧은 이름, 유니코드 수학 기호, 약어 등)이 있으며, 이는 러스트의 스타일과 꽤 다르다. 개인적으로는 좀 낯설지만 바꾸려 하지 않았다. 스타일의 일관성과 호환성이 개인적 선호보다 중요하다.
마지막으로 같은 사실의 더 단순한 단방향 버전도 추가한다. 정확한 논리적 동치 대신, `hi < lo`를 알면 곧바로 집합이 비었다고 결론내릴 수 있게 해주는 보조정리다. 이 방향만 필요한 증명에서 일일이 “양방향 동치”를 다시 세울 필요가 없게 해준다:
lemma toSet_eq_empty_of_hi_lt_lo {r : IntRange} (h : r.hi < r.lo) :
r.toSet = ∅ := (toSet_eq_empty_iff r).mpr h
이 조각들은 산술적 뷰(`lo`, `hi`)를 집합 뷰(`Set.Icc lo hi`)에 연결하고, 임시방편 조건들을 표준적이고 증명 친화적인 Mathlib 사실들로 대체한다.
다음으로, Claude는 비어 있지 않은 구간의 서브타입과 집합으로의 강제변환(coercion)을 정의한다:
/
abbrev NR := { r : IntRange // r.nonempty } /
instance : Coe IntRange (Set Int) where coe := toSet
> 추신(Aside): Lean에는 이름을 정의하는 두 방법 `def`와 `abbrev`가 있다. 어떤 것을 별도의 객체로 취급하고 필요할 때 전개(unfold)되길 원한다면 `def`를 사용하라. 단지 기존 표현의 짧은 별칭만 원한다면 `abbrev`를 쓰라. 이번 프로젝트에서 `abbrev NR := {r : IntRange // r.nonempty}`는 “비어 있지 않은 구간”의 편리한 약칭일 뿐, 새로운 타입을 만든 게 아니다.
이제 메인 `RangeSetBlaze` 자료구조(Claude는 처음에 `RangeList`라 불렀다)를 보자:
def before (a b : IntRange) : Prop := a.hi + 1 < b.lo
scoped infixl:50 " ≺ " => IntRange.before
/ /
structure RangeList where
ranges : List IntRange
all_nonempty : ∀ r ∈ ranges, r.nonempty
pairwise_gaps : List.Pairwise IntRange.before ranges
이는 `RangeList`(`RangeSetBlaze`)를 **데이터**와 **증명**으로 이루어진 구조체로 정의한다.
- 데이터는 단순히 정수 구간의 리스트다.
- 증명은 두 가지 성질을 보장한다:
1) 리스트의 모든 구간은 비어 있지 않다(`lo ≤ hi`).
2) 구간들은 정렬되어 있고 서로 떨어져 있다(불연속). — 형식적으로는, 어떤 앞선 구간 `a`와 뒤의 구간 `b`에 대해 `a.hi + 1 < b.lo`가 성립한다.
이 “규칙 5” 버전은 초기 “규칙 4” 형태보다 더 깔끔하고 수학적이다. “정렬 및 불연속” 속성을 선언적으로 표현하며, 인덱스 관리 같은 번거로움은 Lean 내장 `Pairwise` 술어가 자동으로 처리한다.
Claude의 `Basic.lean` 리라이트는 인상적이었지만, 완전히 만족스럽진 않았다. Rust 라이브러리와 더 가깝고 증명 효율도 좋은 설계로 한 번 더 다듬도록 요청했다:
- `RangeList`를 Rust 프로젝트와 일치하도록 `RangeSetBlaze`로 이름 변경.
- `before`(`≺`)는 오직 **비어 있지 않은 구간**에 대해서만 정의(빈 구간은 애초에 등장하지 않으므로).
- `ranges` 필드는 **비어 있지 않은 구간**(`NR`)의 리스트로 변경.
- 두 개의 별도 증명 필드를, `≺` 표기와 `Pairwise`로 정의한 단일 필드 `ok`로 교체.
- `deriving Repr`로 출력 가능하게.
그 결과 내가 원하던 정확한 형태가 나왔다:
def before (a b : NR) : Prop := a.val.hi + 1 < b.val.lo
scoped infixl:50 " ≺ " => NR.before
/
structure RangeSetBlaze where
ranges : List NR
ok : List.Pairwise (· ≺ ·) ranges
deriving Repr
이제 타입이 **구성상 비어 있지 않음**을 보장하고, `Pairwise` 불변식은 간결하고 표현력이 있으며, 이름도 Rust 라이브러리와 일치한다.
최종 규칙 5의 `Basic.lean`이나 [전체 프로젝트](https://github.com/CarlKCarlK/range-set-blaze-lean/tree/c03a491)는 GitHub에서 볼 수 있다.
> 추신(Aside). “비어 있지 않음”을 타입 안으로 밀어 넣고 Mathlib에 기대는 방식은, 내 첫 시도에서 만난 막다른 길을 피하게 해주었다. 타입이 빈 구간을 배제하니, Lean의 **증명 자동화**는 매번 그 경우를 고려할 필요가 없어져 단순화와 추론 도구가 더 안정적으로 작동한다.
자, 이렇게 해서 AI를 사용해 알고리즘의 정확성을 증명하는 첫 다섯 가지 규칙을 살펴보았다. 파트 2에서는 규칙 6~9와, 결과물로 연결되는 더 많은 GitHub 링크를 다룰 것이다. 미리보기로 규칙 6의 첫 프롬프트를 아래에 남긴다.
> 추신(Aside): 파트 2나 이후 글에 관심이 있다면 [Medium에서 나를 팔로우](https://medium.com/@carlmkadie)하라. 나는 Rust/Python 과학 프로그래밍, 머신러닝, 통계에 관해 쓴다. 대략 한 달에 한 편 정도 올린다.
### 규칙 6 미리보기: AI에게 장난감 알고리즘을 발명·증명하게 하라 — 단순하고 느리지만 정확하게
첫 프롬프트:
Define an internalAddA method on RangeSetBlaze in Lean.
The method should take:
a RangeSetBlaze, and
a possibly empty IntRange.
It should return a new RangeSetBlaze whose set equals the union
of the set of the original RangeSetBlaze and the set of the input range.
Use the existing definitions of IntRange, NR, before (≺), and
RangeSetBlaze. Ensure the result remains valid (the list of nonempty
ranges stays sorted and disjoint).
Include any needed helper definitions or lemmas, and a simple correctness
lemma stating:
(internalAddA s r).toSet = s.toSet ∪ r.toSet
Also:
Add small, concrete examples and sanity checks in Main.lean that exercise internalAddA:
Construct a few IntRange/NR values (empty, touching, overlapping, and disjoint).
Build a small RangeSetBlaze, call internalAddA with each case, and show results via #eval or IO.println.
Include at least two example-style lemmas that compile (e.g., facts about membership after internalAddA).
Make sure everything compiles with lake build. If you add a main in Main.lean, ensure it runs under lake env lean --run Main.lean (optional).
Process constraints:
Work in minimal, compiling steps. After each change, recompile.
If you hit a loop (e.g., repeating edits with no new errors resolved), stop after 2 compile cycles without progress and explain what’s blocking you.
Prefer Mathlib lemmas over ad-hoc proofs. Keep proofs short and readable.
Keep naming and notation consistent with earlier sections.
At the end, output:
A brief rationale of the approach (1–3 sentences).
The updated Lean snippets (only the changed/added parts), clearly labeled with filenames and line anchors if relevant.
The exact commands you used to compile/run.
A “next improvements” list (e.g., edge cases, perf, stronger lemmas).
If you're having problems with corrupted files be very careful
to avoid creating UTF8-BOM (create an AGENTS.md to remember this)