원-핫 인코딩, 내적과 행렬 곱, 마르코프 모델에서 출발해 어텐션, 임베딩, 위치 인코딩, 멀티헤드, 스킵 연결, 인코더·디코더·크로스 어텐션, 토큰화와 BPE, 오디오 입력까지 트랜스포머를 바닥부터 직관적으로 설명한다.
나는 트랜스포머를 깊게 파보는 일을 몇 년이나 미뤄왔다. 결국 ‘무엇이 돌아가게 만드는가를 모른다’는 불편함이 너무 커졌다. 이 글은 그 다이브의 기록이다.
트랜스포머는 2017년 발표된 이 논문에서 시퀀스 변환(sequence transduction)—하나의 기호 시퀀스를 다른 시퀀스로 바꾸는 작업—을 위한 도구로 소개되었다. 가장 대중적인 예는 번역, 예를 들어 영어를 독일어로 바꾸는 일이다. 이후 트랜스포머는 시퀀스 완성—시작 프롬프트를 주면 같은 맥락과 스타일로 이어 쓰기—에도 쓰이도록 변형되었다. 자연어 처리의 연구와 제품 개발에서 없어서는 안 될 도구가 되었다.
시작하기 전에 한 가지 예고. 행렬 곱셈을 자주 다룰 것이고, 역전파(모델을 학습시키는 알고리즘)도 살짝 건드릴 것이다. 하지만 미리 알 필요는 없다. 필요한 개념을 하나씩, 설명과 함께 추가해 갈 것이다.
짧은 여정은 아니지만, 다녀온 것이 기쁘길 바란다.
태초에 단어가 있었다. 정말, 엄청나게 많은 단어가. 첫 단계는 단어를 숫자로 바꿔 수학을 할 수 있게 만드는 일이다.
목소리 명령에 반응하는 컴퓨터를 만든다고 해 보자. 소리의 시퀀스를 단어의 시퀀스로 변환(혹은 트랜스듀스)하는 트랜스포머를 만드는 게 우리의 일이다.
우리는 먼저 작업할 기호의 집합, 즉 어휘(vocabulary)를 고른다. 우리의 경우 입력 시퀀스(음성)를 위한 기호 집합 하나, 출력 시퀀스(단어)를 위한 기호 집합 하나, 이렇게 두 개가 있을 것이다.
일단 영어를 다룬다고 하자. 영어에는 수만 개의 단어가 있고, 여기에 컴퓨터 관련 용어 몇천 개를 더하면 어휘 크기는 대략 십만 단위가 된다. 단어를 숫자로 바꾸는 한 가지 방법은 1부터 번호를 붙이는 것이다. 그러면 단어 시퀀스를 숫자 리스트로 표현할 수 있다.
예를 들어 어휘 크기가 3인 아주 작은 언어를 생각해 보자: files, find, my. 각 단어에 숫자를 할당할 수 있다. 이를테면 files = 1, find = 2, my = 3. 그러면 [ find, my, files ]라는 단어 시퀀스로 구성된 문장 "Find my files"는 [2, 3, 1]이라는 숫자 시퀀스로 표현된다.
이 방식도 타당하지만, 컴퓨터가 더 다루기 쉬운 다른 형식이 있다. 바로 원-핫 인코딩(one-hot encoding)이다. 원-핫 인코딩에서는 기호를 어휘 크기와 같은 길이의 거의 0으로만 이루어진 배열로 표현하고, 오직 하나의 원소만 1이 된다. 배열의 각 원소가 서로 다른 기호에 대응한다.
다르게 생각하면, 각 단어는 여전히 고유한 번호를 받지만 이제 그 번호는 배열의 인덱스다. 위의 예를 원-핫 표기법으로 나타내면 다음과 같다.
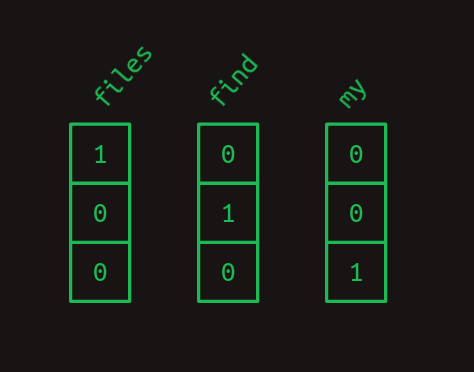
따라서 "Find my files"라는 문장은 원-핫 벡터들의 시퀀스가 되고, 이들을 차곡차곡 쌓으면 2차원 배열처럼 보이기 시작한다.

참고로, 나는 "1차원 배열"과 "벡터"를 같은 의미로, "2차원 배열"과 "행렬"을 같은 의미로 쓸 것이다.
원-핫 표현이 특히 유용한 이유 중 하나는 내적을 계산할 수 있게 해 주기 때문이다. 내적(dot product)은 다른 이름으로는 inner product, scalar product라고도 불린다. 두 벡터의 내적은 대응하는 원소끼리 곱한 뒤 그 값을 모두 더하면 된다.

원-핫 단어 표현을 다룰 때 내적은 특히 유용하다. 어떤 원-핫 벡터와 자기 자신과의 내적은 1이다.

그리고 어떤 원-핫 벡터와 다른 원-핫 벡터의 내적은 0이다.

앞의 두 예는 내적이 유사도를 측정하는 데 어떻게 쓰일 수 있는지를 보여준다. 또 다른 예로, 여러 단어가 가중합으로 섞여 있는 값을 나타내는 벡터를 생각해 보자. 여기에 하나의 원-핫 단어를 내적하면 그 단어가 얼마나 강하게 나타나 있는지를 알 수 있다.

내적은 행렬 곱셈의 구성 요소다. 행렬 곱셈은 두 개의 2차원 배열을 아주 특정한 방식으로 결합한다. 첫 번째 행렬을 A, 두 번째를 B라 하자. 가장 단순한 경우, A가 한 행만 갖고 B가 한 열만 갖는다면, 행렬 곱셈의 결과는 두 벡터의 내적이다.
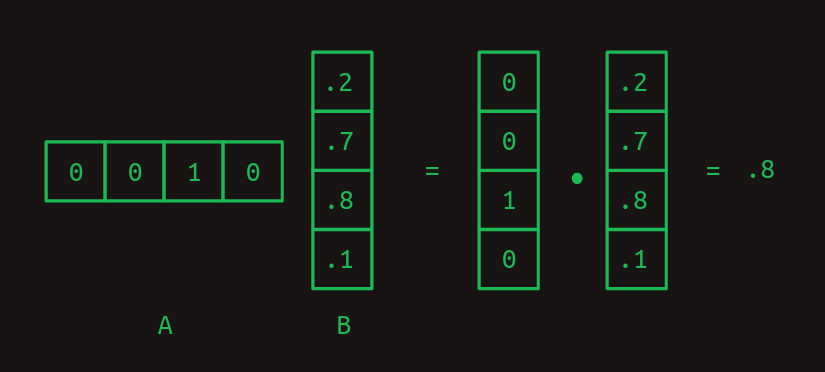
A의 열의 개수와 B의 행의 개수는 서로 같아야 내적이 성립한다.
A와 B가 커지면 행렬 곱셈은 조금 어지러워진다. A에 여러 행이 있다면, B와 각 행의 내적을 따로 계산한다. 결과는 A의 행 개수만큼 행을 갖는다.
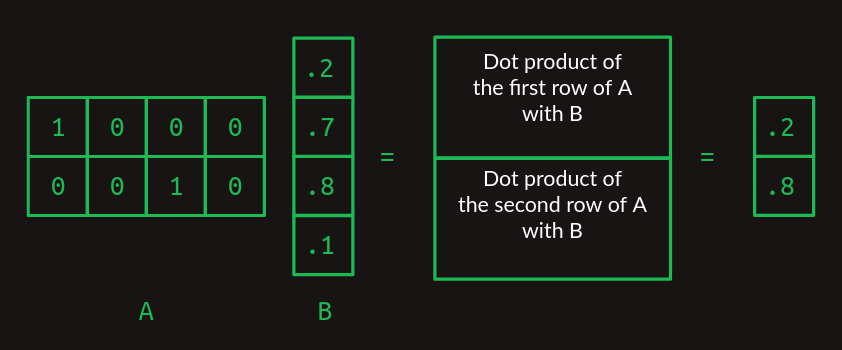
B에 여러 열이 있다면, 각 열과 A의 내적을 계산해 결과를 열 방향으로 쌓는다.
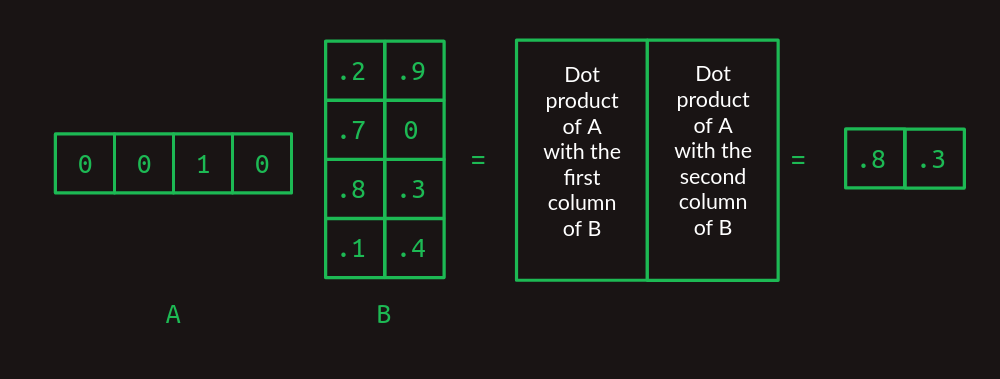
이제 A의 열 개수와 B의 행 개수만 같다면 임의의 두 행렬을 곱할 수 있다. 결과는 A의 행 개수와 B의 열 개수를 갖는다.
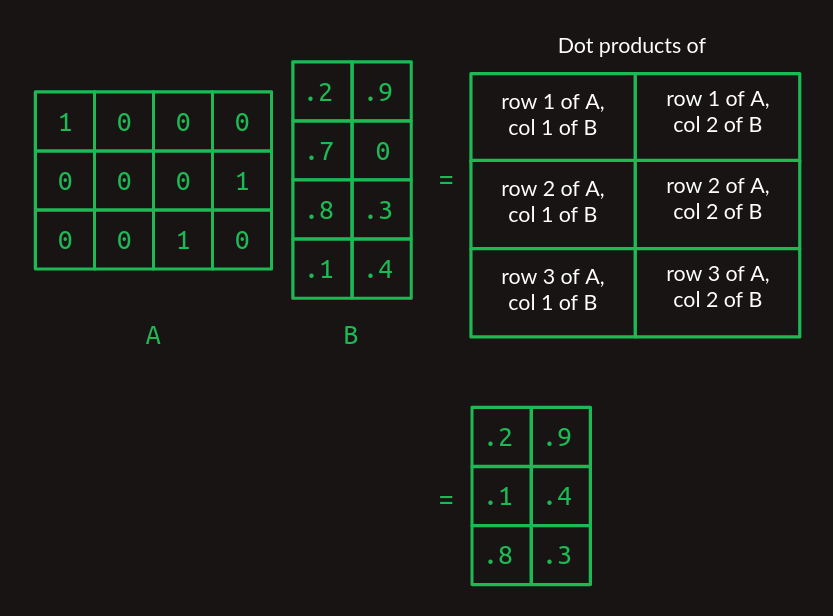
처음 보면 불필요하게 복잡해 보일지 모르지만, 곧 그 값어치를 보게 된다.
여기서 행렬 곱셈이 조회 테이블처럼 작동한다는 점을 보자. A 행렬은 원-핫 벡터를 차곡차곡 쌓은 것이다. 각 행은 첫 번째, 네 번째, 세 번째 열이 각각 1이다. 행렬 곱셈을 해 보면, 이는 B 행렬의 첫 번째 행, 네 번째 행, 세 번째 행을 그 순서로 뽑아오는 역할을 한다. 원-핫 벡터를 써서 행렬의 특정 행을 뽑아오는 이 트릭이 트랜스포머의 핵심이다.
이제 행렬은 잠시 접어두고, 우리가 정말로 관심 있는 ‘단어 시퀀스’로 돌아가자. 음성 제어 인터페이스를 개발한다고 할 때, 딱 세 가지 명령만 처리한다고 해 보자.
우리의 어휘 크기는 이제 7이다:
{directories, files, me, my, photos, please, show}.
시퀀스를 표현하는 한 가지 유용한 방법은 전이(transition) 모델이다. 어휘의 각 단어에 대해, 다음 단어가 무엇일지의 가능성을 보여준다. 사용자가 절반은 photos를, 30%는 files를, 나머지는 directories를 묻는다면 전이 모델은 다음과 같다. 어떤 단어에서든 빠져나가는 전이의 합은 항상 1이다.
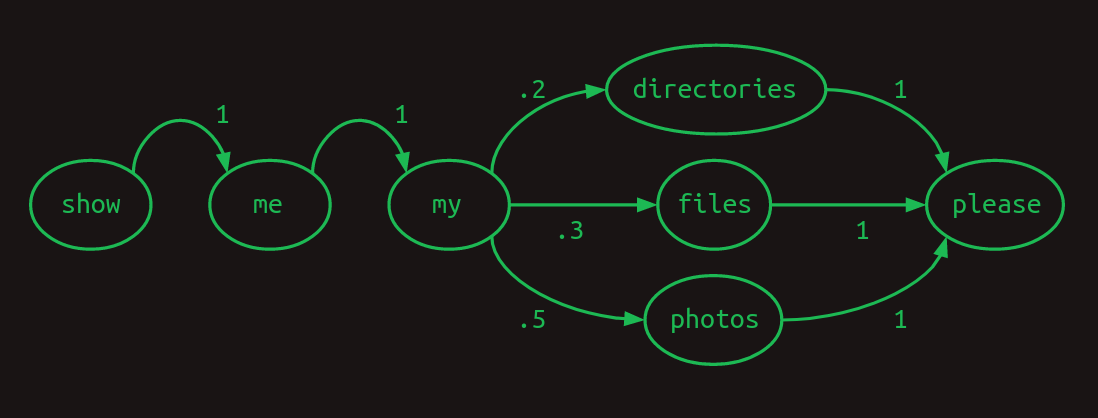
이 전이 모델은 **마르코프 연쇄(Markov chain)**라고 한다. 마르코프 성질, 즉 다음 단어의 확률이 ‘최근의 단어들’에만 의존한다는 성질을 만족하기 때문이다. 더 정확히, 가장 최근의 단어 하나만 본다면 1차 마르코프 모델이다. 최근 두 단어를 본다면 2차 마르코프 모델이다.
행렬로부터의 휴식은 여기까지. 마르코프 연쇄는 행렬로 아주 편리하게 표현된다. 원-핫 벡터를 만들 때 사용한 인덱싱을 그대로 쓰면, 각 행은 어휘의 한 단어를 나타낸다. 각 열도 마찬가지다. 전이 행렬은 행렬을 조회 테이블처럼 취급한다. 관심 있는 단어에 대응하는 행을 찾고, 각 열의 값이 그 단어가 다음에 나올 확률이다. 행렬의 각 원소는 확률이므로 0과 1 사이에 있다. 그리고 확률의 합은 1이므로 각 행의 합은 1이다.
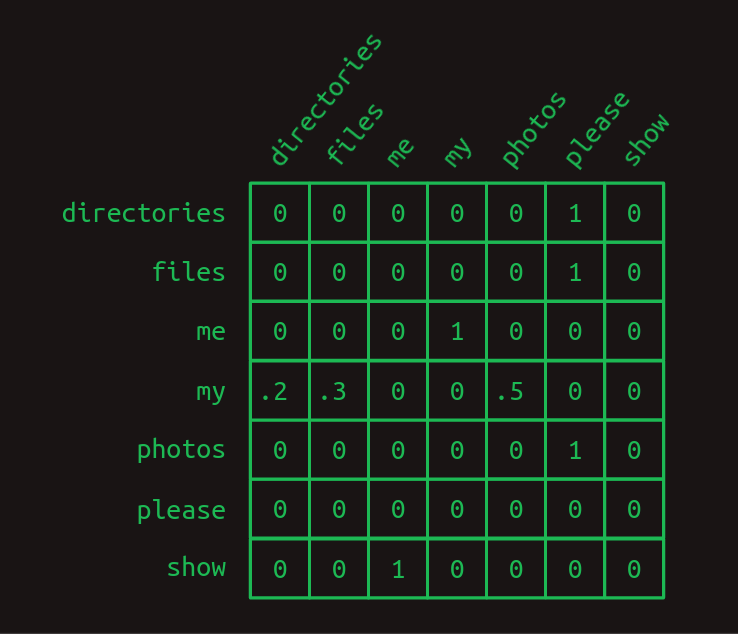
전이 행렬을 보면 우리의 세 문장 구조가 뚜렷하다. 전이 확률의 거의 전부가 0이나 1이다. 마르코프 연쇄에서 분기(branch)가 생기는 지점은 오직 하나, my 다음에 directories, files, _photos_가 각각 다른 확률로 나타나는 부분뿐이다. 그 외에는 다음 단어에 대한 불확실성이 없다. 이는 전이 행렬에 대부분 1과 0이 들어 있는 것으로 반영된다.
원-핫 벡터와 행렬 곱셈을 이용해, 특정 단어와 관련된 전이 확률을 뽑아오는 트릭을 다시 쓸 수 있다. 예를 들어 my 다음에 올 단어의 확률만 보고 싶다면, _my_를 나타내는 원-핫 벡터를 만들고 전이 행렬과 곱하면 된다. 해당 행이 뽑혀서 다음 단어의 확률분포가 나온다.
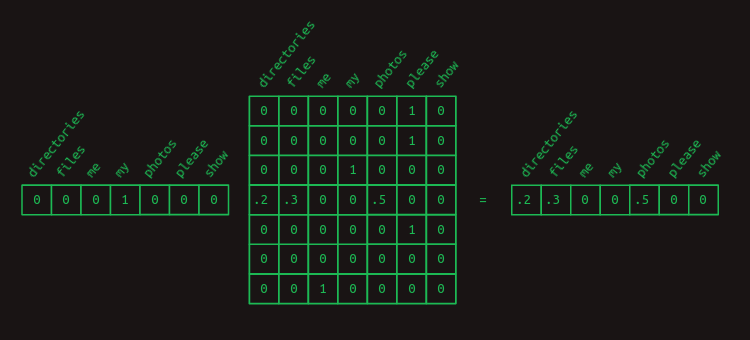
현재 단어 하나만 보고 다음 단어를 예측하는 것은 어렵다. 첫 음만 듣고 곡 전체를 맞추라는 것과 비슷하다. 두 음만 더 알 수 있어도 가능성은 훨씬 좋아진다.
다음은 다른 장난감 언어 모델이다. 이번엔 두 문장만 보고, 비율은 40/60이다.
1차 모델을 마르코프 연쇄로 나타내면 다음과 같다.
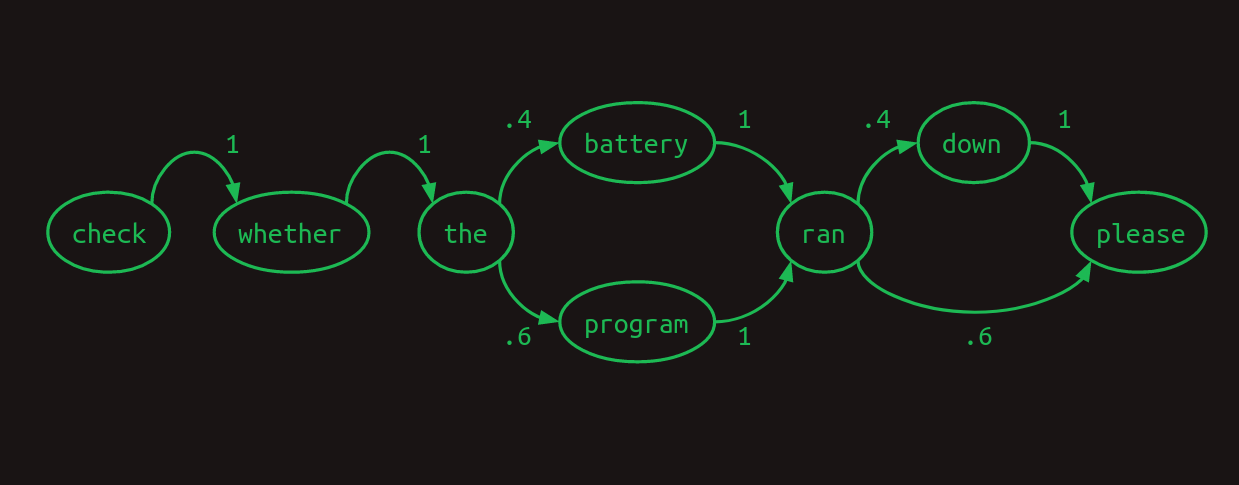
여기서 최근 단어 하나가 아니라 두 단어를 볼 수 있다면 더 잘할 수 있음을 알 수 있다. _battery ran_을 보면 다음 단어는 _down_이고, _program ran_을 보면 다음은 _please_라는 것을 안다. 모델의 분기가 하나 사라져 불확실성이 줄고 확신이 커진다. 최근 두 단어를 본다면 2차 마르코프 모델이 된다. 다음 단어 예측의 문맥이 더 풍부해진다. 2차 마르코프 연쇄는 그리기가 더 어렵지만, 그 가치가 드러나는 연결은 다음과 같다.
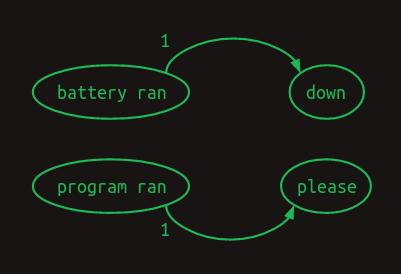
차이를 강조하기 위해 1차 전이 행렬을 보자.
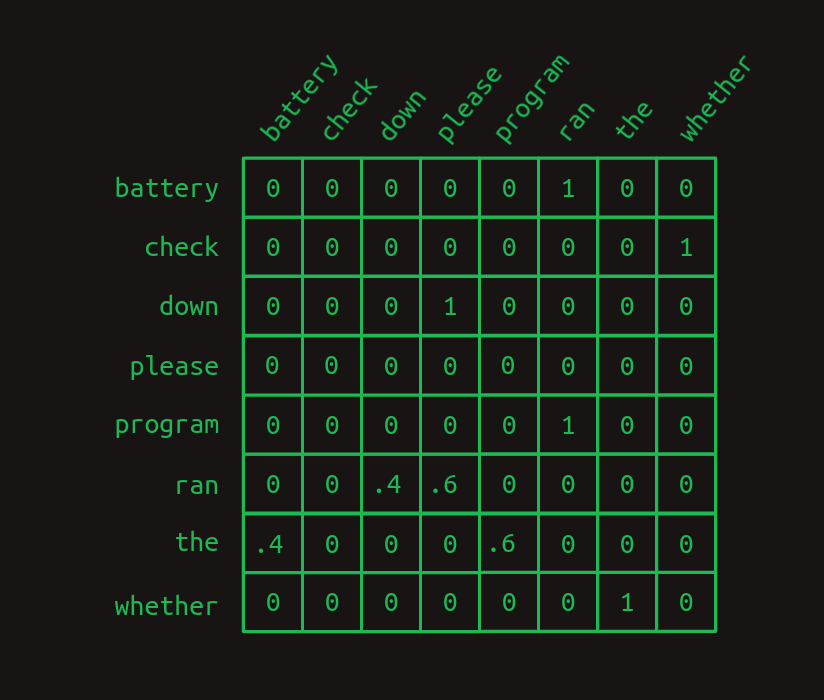
그리고 2차 전이 행렬은 다음과 같다.

2차 행렬에는 가능한 단어 조합마다 별도의 행이 있음을 보라(대부분은 표시하지 않았다). 어휘 크기가 N이면 전이 행렬의 행은 N^2개가 된다.
얻는 것은 ‘더 높은 확신’이다. 2차 모델에서는 1이 더 많고 분수(0과 1 사이)가 더 적다. 분기가 있는 행이 단 하나뿐이다. 직관적으로도, 한 단어만 볼 때보다 두 단어를 보면 문맥이 늘어나 다음 단어 추측의 정보가 증가한다.
2차 모델은 뒤로 두 단어만 보면 다음 단어를 결정할 수 있을 때 잘 작동한다. 더 멀리 봐야 한다면? 다음 두 문장이 동일한 빈도로 나타나는 또 다른 모델을 생각해 보자.
이 예에서는 ran 다음 단어를 결정하려면 과거로 8단어까지 거슬러 올라가야 한다. 2차 모델을 개선하려면 3차, 그 이상도 고려할 수 있다. 하지만 어휘가 크면 창의성과 난폭한 힘이 동시에 필요하고, 순진하게 8차 모델을 만들면 N^8 행이 되어 현실적이지 않다.
대신 약간 영리한 방법을 쓰자. 2차 모델이되, ‘가장 최근 단어’와 그 앞의 각 단어의 조합을 고려한다. 여전히 두 단어씩만 보므로 2차이지만, 더 멀리까지 뻗어가 **장거리 의존성(long range dependencies)**을 포착한다. 스킵을 허용하는 2차 모델과 ‘완전한 n차 모델’의 차이는 대부분의 순서 정보와 앞선 단어들의 조합을 버린다는 점이다. 남는 것만으로도 상당히 강력하다.
이제 마르코프 연쇄는 전혀 도움이 안 되지만, 앞선 단어 쌍 각각과 그 다음 단어의 연결은 여전히 표현할 수 있다. 여기서는 수치 가중치를 생략하고, 0이 아닌 가중치의 화살표만 표시했다. 더 큰 가중치는 더 굵은 선으로 표시했다.
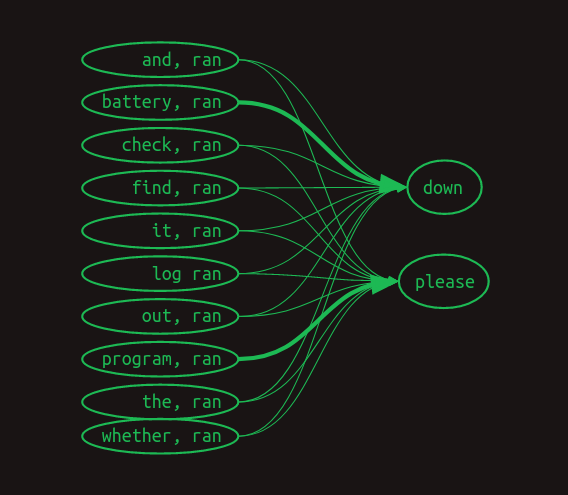
전이 행렬로 보면 다음과 같을 수 있다.

여기서는 ran 다음 단어를 예측하는 데 관련된 행만 보였다. 가장 최근 단어(ran)가 어휘의 다른 각 단어 앞에 왔을 때의 경우를 보여준다. 관련 값만 표시했다. 빈 칸은 모두 0이다.
가장 먼저 보이는 것은, 이제 ran 다음 단어를 예측할 때 한 줄이 아니라 여러 줄을 본다는 점이다. 이제 우리는 마르코프 영역을 벗어났다. 각 행이 더 이상 ‘특정 시점의 시퀀스 상태’를 의미하지 않는다. 대신 특정 시점의 시퀀스를 설명할 수 있는 여러 피처(feature) 중 하나를 나타낸다. 최근 단어와 그 이전의 각 단어의 조합은 적용 가능한 행들의 모음, 어쩌면 아주 큰 모음이 된다. 의미가 바뀌었으므로, 행렬의 각 값은 더 이상 ‘확률’이 아니라 ‘표(vote)’가 된다. 표를 합산하고 비교해 다음 단어를 정한다.
다음으로 보이는 것은, 대부분의 피처는 중요하지 않다는 것이다. 대부분의 단어는 두 문장 모두에 등장하므로, 그들이 등장했다는 사실은 다음을 예측하는 데 도움이 되지 않는다. 그들의 값은 모두 0.5다. 유일한 예외는 _battery_와 _program_이다. 구분하려는 두 경우에 대해 1과 0의 가중치가 붙는다. 피처 _battery, ran_은 ‘_ran_이 가장 최근 단어이고 _battery_가 그보다 앞 어딘가에 있었다’는 뜻이다. 이 피처는 _down_에 1, _please_에 0의 가중치를 갖는다. 마찬가지로 _program, ran_은 그 반대의 가중치를 갖는다. 이 구조는 문장 앞서 등장한 이 두 단어의 존재가 다음 단어를 결정하는 데 핵심임을 보여준다.
이러한 단어-쌍 피처를 다음 단어 추정으로 바꾸려면, 관련된 모든 행의 값을 합치면 된다. 열 방향으로 합하면, _Check the program log and find out whether it ran_은 대부분 0이고 _down_이 4, _please_가 5가 된다. _Check the battery log and find out whether it ran_도 비슷하지만 _down_이 5, _please_가 4다. 합이 가장 큰 단어를 다음으로 선택하면, 8단어 깊이의 의존성이 있어도 정답을 맞힌다.
가만히 생각해 보면, 이 결과는 좀 찜찜하다. 4 대 5라는 표 차이는 작다. 모델이 생각만큼 확신하지 못한다는 신호다. 더 큰, 자연스러운 언어 모델에서는 이런 미세한 차이가 통계적 잡음에 쉽게 묻힐 수 있다.
무익한 피처의 표를 솎아내어 예측을 더 선명하게 만들 수 있다. _battery, ran_과 _program, ran_만 남기고 나머지는 제거하자. 관련된 행들을 전이 행렬에서 뽑아내는 방식은 ‘현재 활성화된 피처를 표시한 벡터’와 행렬을 곱하는 것임을 기억하자. 지금까지는 아래와 같은 암묵적 피처 벡터를 써 왔다.
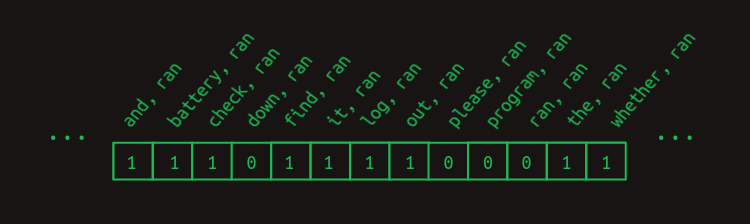
이는 _ran_과 그 앞에 왔던 각 단어의 조합에 대해 1을 포함한다. 뒤에 오는 단어들은 피처에 포함되지 않는다(다음 단어 예측 문제에서는 아직 보지 않았고, 다음을 예측하는 데 쓰면 반칙이다). 그 외 모든 조합은 이 예에서 0이므로 무시해도 된다.
결과를 개선하려면, 무익한 피처들을 0으로 강제하는 **마스크(mask)**를 만들면 된다. 숨기지 않을 위치에는 1, 숨길 위치에는 0을 넣은 벡터다. 우리의 경우 도움이 된 _battery, ran_과 _program, ran_을 제외한 모든 것을 마스킹하고 싶다.

마스크를 적용하려면 두 벡터를 원소별로 곱한다. 마스크되지 않은 위치의 피처 값은 1을 곱해 그대로 남고, 마스크된 위치의 값은 0을 곱해 0이 된다.
마스크는 전이 행렬의 많은 부분을 가린다. _battery_와 _program_을 제외한 모든 것과 _ran_의 조합을 숨겨, 중요한 피처만 남긴다.

무익한 피처를 마스킹하면 다음 단어 예측이 훨씬 강해진다. 문장 앞부분에 _battery_가 있으면 ran 다음은 _down_이 가중치 1, _please_는 0으로 예측된다. 이전에는 25%의 차이었지만 이제는 무한대의 차이(0과 1)이 되었다. 다음 단어가 무엇인지 의심의 여지가 없다. _program_이 앞에 있으면 _please_에 대해서도 같은 수준의 강한 예측이 나온다.
이 ‘선택적 마스킹’ 과정이 바로 트랜스포머 원 논문의 제목에 나온 **어텐션(attention)**이다. 지금까지 설명한 것은 논문에서의 구현을 ‘근사’한 것이다. 핵심 개념은 포착했지만, 세부는 다르다. 곧 그 간극을 메울 것이다.
여기까지 오느라 수고했다. 여기서 멈춰도 좋다. ‘선택적-스킵 허용-2차’ 모델은 적어도 디코더 측면에서 트랜스포머가 무엇을 하는지 생각하는 유용한 방법이다. OpenAI의 GPT-3 같은 생성형 언어 모델이 하는 일을 1차 근사로 포착한다. 완전한 이야기는 아니지만, 중심축은 잡고 있다.
이제부터는 이 직관적 설명과 실제 구현 사이의 간극을 좀 더 메운다. 주로 세 가지 현실적 고려가 이득을 준다.
신경망 설계의 과학이 ‘미분 가능한 블록을 만드는 일’이라면, 그 예술은 ‘그래디언트가 너무 급하게 변하지 않고 모든 방향에서 비슷한 크기’가 되도록 블록을 쌓는 일이다.
피처 가중치는 학습 데이터에서 각 단어쌍/다음 단어 전이가 얼마나 자주 일어나는지를 세어 만드는 등 비교적 간단할 수 있다. 하지만 어텐션 마스크는 그렇지 않다. 지금까지는 마스크 벡터를 허공에서 꺼내 왔다. 트랜스포머가 어떻게 관련 마스크를 찾는지가 중요하다. 조회 테이블을 쓰는 것이 자연스럽겠지만, 우리는 모든 것을 행렬 곱으로 표현하는 데 집중하고 있다. 위에서 소개한 것과 같은 조회 방법을 쓰자. 모든 단어에 대한 마스크 벡터를 행으로 쌓아 하나의 행렬로 만들고, 가장 최근 단어의 원-핫 표현으로 관련 마스크를 뽑아낸다.
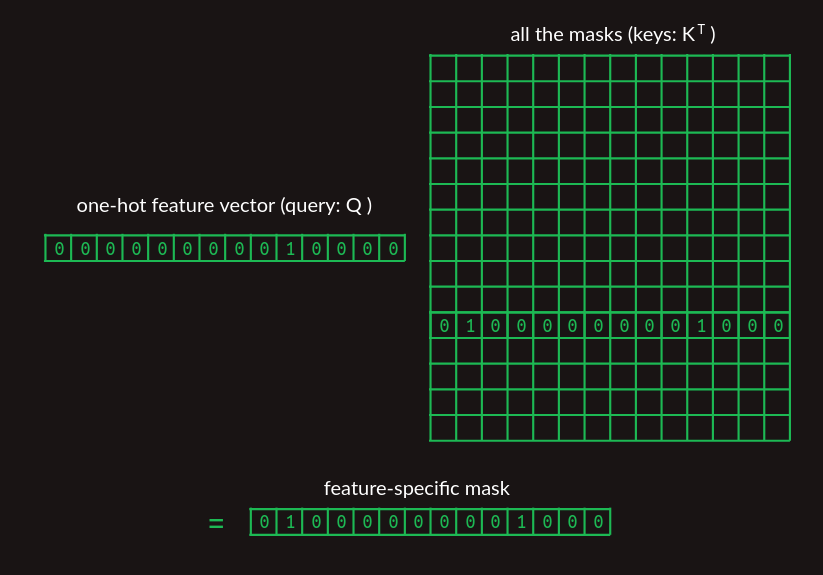
마스크 벡터 모음을 보여주는 행렬에서는, 보기 쉽게 지금 뽑아내려는 것만 표시했다.
드디어 논문과 연결할 수 있는 지점에 왔다. 이 마스크 조회는 어텐션 방정식의 QK^T 항으로 표현된다.
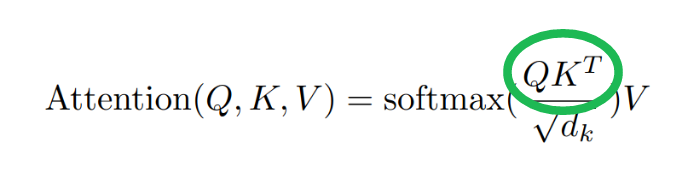
쿼리 Q는 관심 피처를, 행렬 K는 마스크의 컬렉션을 의미한다. 마스크를 행이 아니라 ‘열’로 저장했기 때문에 곱하기 전에 전치(T 연산자)가 필요하다. 곧 중요한 수정이 더해지겠지만, 이 수준에서는 트랜스포머가 사용하는 ‘미분 가능한 조회 테이블’이라는 개념을 잘 담고 있다.
지금까지 대충 넘어간 또 하나는 전이 행렬을 어떻게 구성하느냐였다. 논리는 설명했지만, 행렬 곱만으로 어떻게 하느냐는 덜 분명했다.
어텐션 결과(가장 최근 단어와 그 앞의 몇 단어를 포함하는 벡터)를 얻었다면, 이를 ‘단어쌍’ 피처로 번역해야 한다. 어텐션 마스킹은 원재료를 제공하지만, 단어쌍 피처 자체를 만들지는 않는다. 이를 위해 완전연결 신경망 한 층을 사용할 수 있다.
신경망 한 층이 어떻게 이런 쌍을 만드는지 보려면, 하나를 손으로 만들어 보자. 인위적으로 깨끗하고 꾸며진 예가 될 것이며, 실제의 가중치와는 닮지 않겠지만, ‘두 단어 조합 피처’를 만들 수 있는 표현력을 보여줄 것이다. 단순하게 하기 위해 이 예에서 주의된 세 단어 battery, program, _ran_에 집중하자.
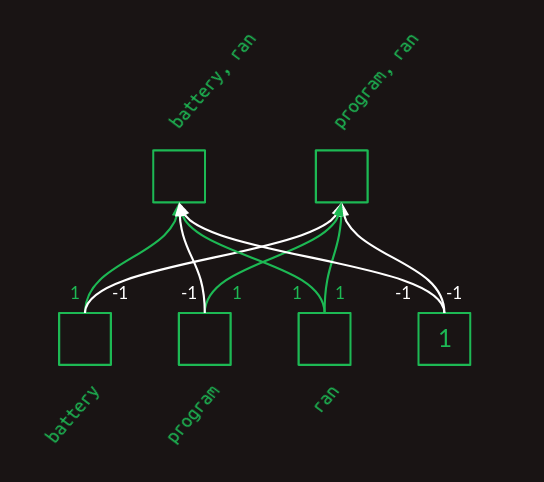
위의 층 다이어그램은 가중치가 각 단어의 존재/부재를 결합해 피처 모음을 만드는 방식을 보여준다. 이는 행렬로도 표현할 수 있다.

그리고 지금까지 본 단어들의 모음을 나타내는 벡터와의 행렬 곱으로 계산할 수 있다.
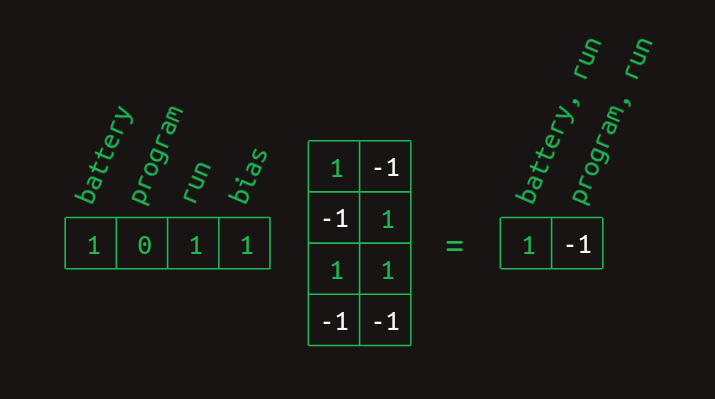
_battery_와 ran 원소는 1이고 _program_은 0이다. bias 원소는 항상 1인데, 신경망의 특성이다. 행렬 곱을 수행하면 _battery, ran_을 나타내는 원소는 1, _program, ran_은 -1이 된다. 다른 경우도 유사하다.
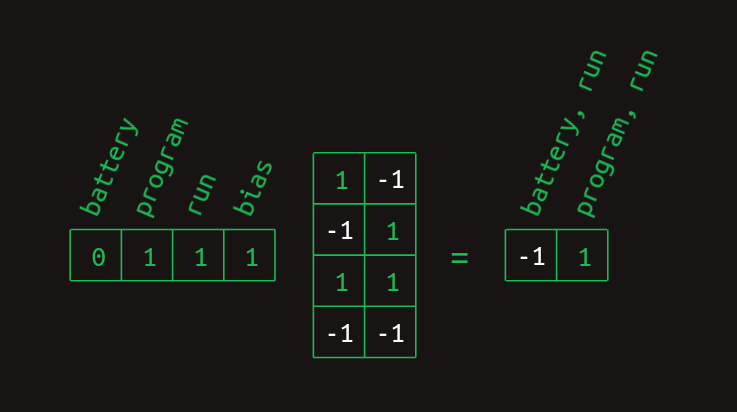
마지막 단계는 렐루(ReLU) 비선형성을 적용하는 것이다. 음수 값을 0으로 바꾼다. 이렇게 두 결과가 정리되어 각 단어 조합 피처의 존재(1)나 부재(0)를 나타내게 된다.
이제 행렬 곱만으로 다단어 피처를 만드는 방법을 갖게 되었다. 처음에는 ‘가장 최근 단어 + 앞선 단어 하나’로 구성된다고 주장했지만, 이 방법을 자세히 보면 다른 피처도 만들 수 있음을 알 수 있다. 피처 생성 행렬을 코드로 박아넣지 않고 학습한다면, 다른 구조도 학습될 수 있다. 이 장난감 예에서도 battery, program, ran 같은 세 단어 조합을 막을 것은 없다. 이런 조합이 충분히 자주 등장하면 표현될 가능성이 높다. 단, 단어가 나타난 순서를 나타낼 방법은 없다(적어도 아직은). 하지만 공기현상(동시 출현)을 이용해 예측하는 데 쓸 수 있다. 심지어 가장 최근 단어를 무시한 조합인 battery, program 같은 것도 쓸 수 있다. 실제로는 이런 종류의 피처들이 만들어질 가능성이 높다. 내가 ‘트랜스포머는 선택적-스킵 허용-2차 시퀀스 모델’이라고 단순화했던 주장이 과도했음을 드러낸다. 더 미묘한 면이 있고, 이제 그 미묘함이 정확히 무엇인지 볼 수 있다. 이것이 마지막 수정은 아닐 것이다.
이 형태의 다단어 피처 행렬은 또 한 번의 행렬 곱을 할 준비가 되었다. 즉, 위에서 개발한 스킵 허용 2차 시퀀스 모델이다. 요약하면, 다음의 순서로
이 어텐션 뒤에 적용되는 피드포워드 처리 단계다. 논문의 식 2는 이를 간결한 수식으로 보여준다.
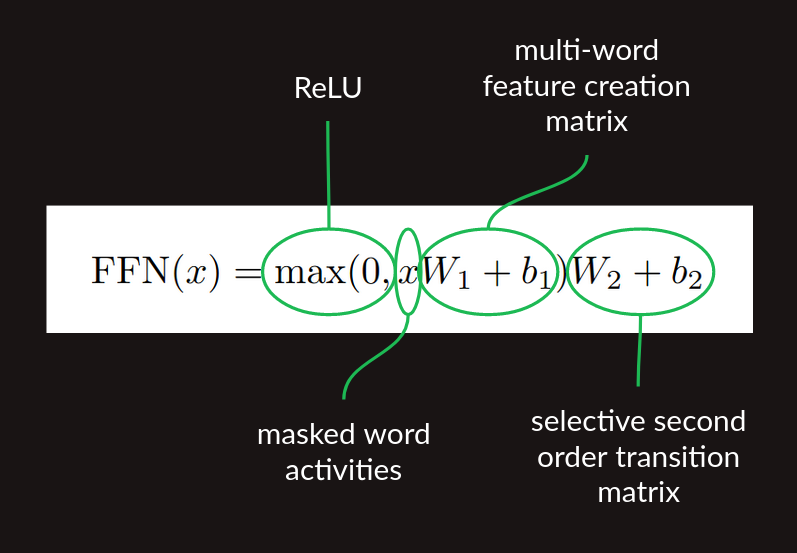
논문 Figure 1의 아키텍처 다이어그램에서는 이것을 Feed Forward 블록으로 묶어 표시한다.
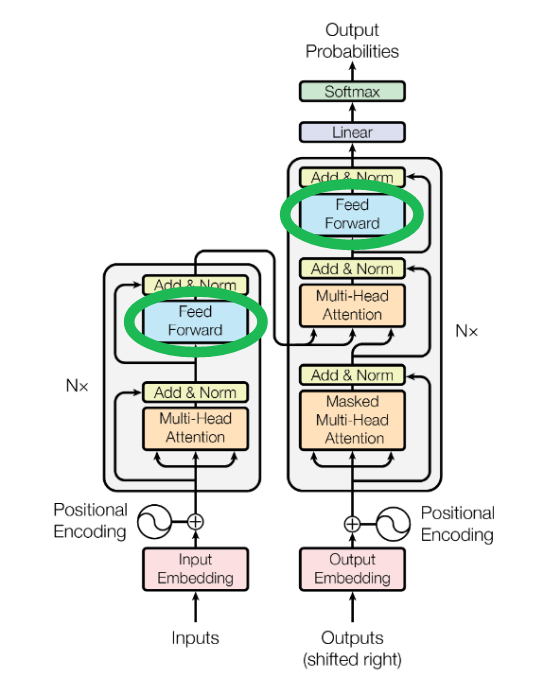
지금까지는 다음 단어 예측만 이야기했다. 디코더가 긴 시퀀스를 생성하게 하려면 몇 가지를 더 추가해야 한다. 첫째는 **프롬프트(prompt)**다. 트랜스포머가 달려 나갈 출발점이자 문맥을 제공할 예문이다. 위 그림에서 오른쪽 열, "Outputs (shifted right)"로 표시된 디코더에 입력된다. 흥미로운 시퀀스를 내는 프롬프트를 고르는 일은 그 자체로 하나의 기술이고, 프롬프트 엔지니어링이라 부른다. 인간이 알고리즘을 돕도록 스스로의 행동을 바꾸는 좋은 예이기도 하다.
디코더가 시작할 부분 시퀀스를 얻으면, 순전파를 한 번 돈다. 결과는 각 위치마다 하나씩, 단어 확률분포의 집합이다. 각 위치에서 어휘의 모든 단어가 다음으로 올 확률이 있다. 이미 확정된 단어들에 대한 확률은 신경 쓰지 않는다. 우리가 정말로 관심 있는 것은 프롬프트의 마지막 다음에 올 단어의 확률분포다. 이를 고르는 방법은 여러 가지가 있지만, 가장 직관적인 건 그리디(greedy)—확률이 가장 높은 단어를 고르는 것이다.
새로 고른 다음 단어를 시퀀스 끝에 추가하고, 디코더 아래의 "Outputs" 자리에 넣은 다음, 이 과정을 지칠 때까지 반복한다.
아직 자세히 설명할 준비가 안 된 한 가지는 또 다른 형태의 마스킹이다. 트랜스포머가 예측할 때 ‘뒤만 보고 앞은 보지 않도록’ 보장하는 장치다. "Masked Multi-Head Attention" 블록에서 적용된다. 나중에 더 분명히 설명할 수 있을 때 다시 보자.
지금까지의 설명대로라면 트랜스포머는 너무 크다. 어휘 크기 N을 50,000이라 하면, 모든 단어쌍과 가능한 모든 다음 단어 사이의 전이 행렬은 5만 열, 5만 제곱(25억) 행, 총 100조 개가 넘는 원소를 갖는다. 현대 하드웨어에도 버거운 크기다.
문제는 행렬 크기만이 아니다. 안정적인 전이 언어 모델을 만들려면 모든 가능한 시퀀스를 최소 몇 번씩 보여주는 학습 데이터가 필요하다. 이는 가장 야심 찬 데이터셋의 용량조차 한참 초과한다.
다행히 두 문제 모두에 대한 우회로가 있다. 임베딩이다.
언어를 원-핫으로 표현하면, 단어마다 벡터의 한 원소가 배정된다. 어휘 크기가 N이면 그 벡터는 N차원 공간이다. 각 단어는 그 공간에서, 원점에서 축 하나를 따라 1만큼 떨어진 점이 된다. 고차원 공간을 그럴듯하게 그리는 건 어렵지만, 아래의 조악한 그림이 있다.
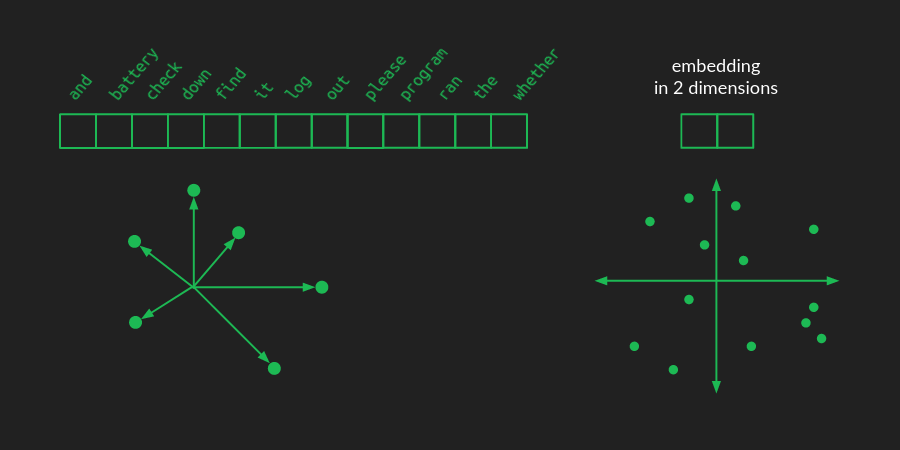
임베딩에서는 그 점들을 더 낮은 차원의 공간으로 재배치(선형대수 용어로는 투영)한다. 위 그림은 2차원 공간으로의 모습이다. 이제 단어를 지정하는 데 N개의 숫자 대신 2개면 된다. 새로운 공간에서 각 점의 좌표 (x, y)다. 장난감 예시에 대한 2차원 임베딩과 몇 단어의 좌표는 다음과 같다.
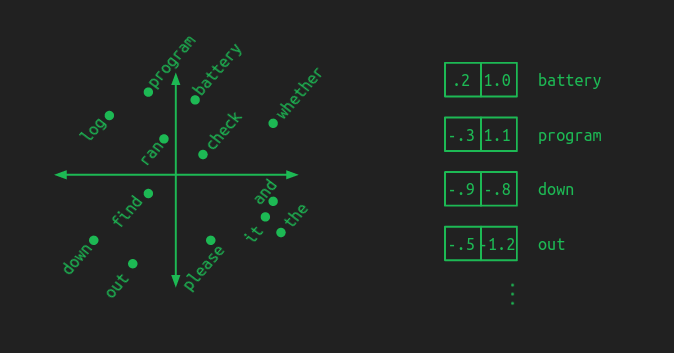
좋은 임베딩은 의미가 비슷한 단어들을 모아 둔다. 임베딩에서 모델은 ‘임베딩 공간’의 패턴을 학습한다. 그러면 어떤 단어에 대해 배운 것이 그 주변의 모든 단어에도 자동으로 적용된다. 이는 필요한 학습 데이터 양을 줄여 주는 부가 이익도 있다. 각 예시가 단어 한 동네 전체에 조금씩 학습을 퍼뜨려 주기 때문이다.
이 그림에서는 핵심 구성요소(battery, log, program)를 한 영역에, 전치사(down, out)를 다른 영역에, 동사(check, find, ran)를 중앙에 배치해 보려 했다. 실제 임베딩에서 이런 묶음이 꼭 명확하거나 직관적이진 않지만, 개념은 같다. ‘가까운’ 단어들은 비슷하게 행동한다.
임베딩은 필요한 파라미터 수를 엄청나게 줄인다. 하지만 차원이 줄수록 원래 단어들에 대한 정보가 더 버려진다. 언어의 풍요로움은 서로 발을 밟지 않게 중요한 개념들을 널찍이 펼칠 공간을 여전히 요구한다. 임베딩 공간의 크기를 선택함으로써, 계산량과 모델 정확도 사이를 절충한다.
원-핫에서 임베딩 공간으로의 투영도 결국 행렬 곱이다. 투영은 행렬의 특기다. N열짜리 원-핫 벡터(1행 N열)에서 2차원 임베딩으로 옮기려면, 투영 행렬은 N행 2열이 된다. 아래와 같다.
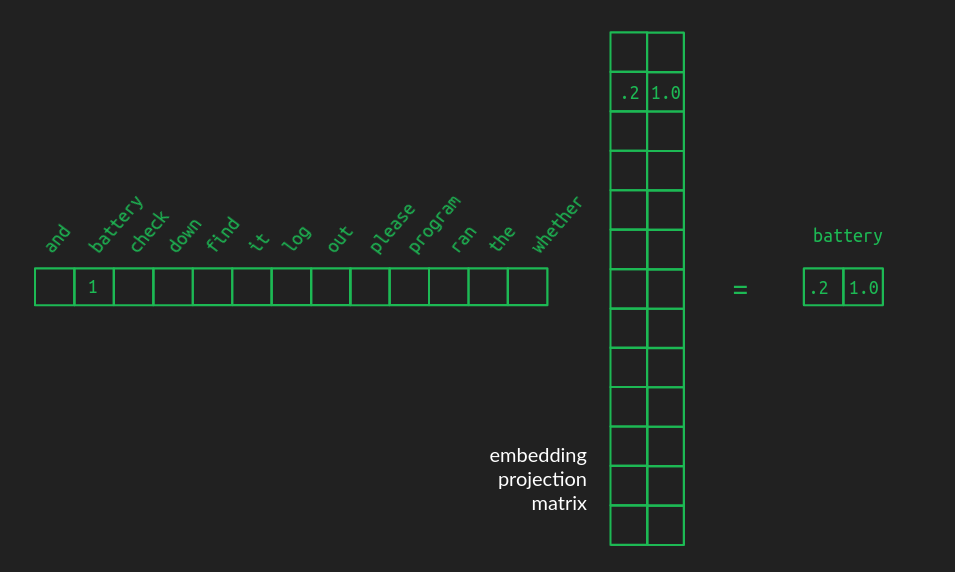
이 예는 _battery_를 나타내는 원-핫 벡터가 그에 대응하는 행(임베딩 공간의 좌표)을 뽑아오는 방식을 보인다. 관계를 분명히 하려고, 원-핫 벡터의 0과 투영 행렬의 사용되지 않는 행은 감췄다. 실제 투영 행렬은 밀집(dense)이며, 각 행은 연관된 단어의 좌표를 담는다.
투영 행렬은 원래의 원-핫 어휘 벡터 모음을 원하는 차원의 공간에서 임의의 구성으로 바꿔줄 수 있다. 가장 큰 요령은 ‘유용한 투영’을 찾는 것이다. 즉, 비슷한 단어들이 잘 모여 있고, 충분한 차원이 있어 서로를 벌려 두는 투영이다. 영어처럼 흔한 언어에 대해 미리 계산된 임베딩도 제법 있고, 트랜스포머의 다른 모든 것처럼 학습 중에 함께 배울 수도 있다.
논문 Figure 1의 아키텍처에서 임베딩은 여기다.
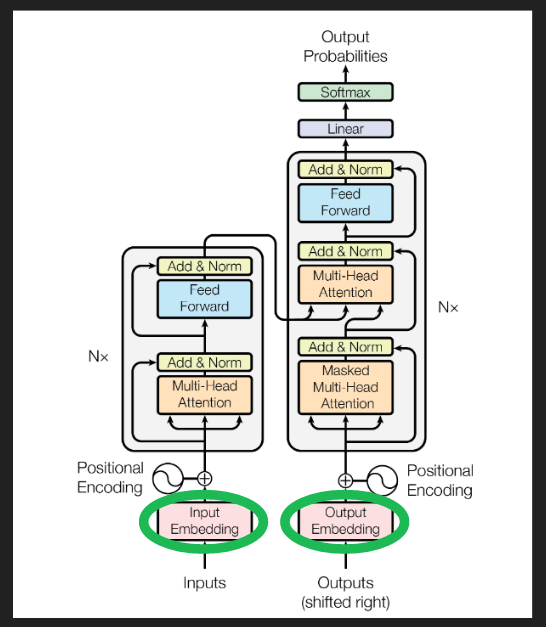
지금까지는, 가장 최근 단어를 제외하면 단어의 위치를 무시한다고 가정했다. 이제 위치 임베딩으로 이를 고치자.
단어의 임베딩 표현에 ‘위치 정보’를 주입하는 방법은 여럿 있지만, 원래 트랜스포머는 ‘원형 흔들림(circular wiggle)’을 더했다.
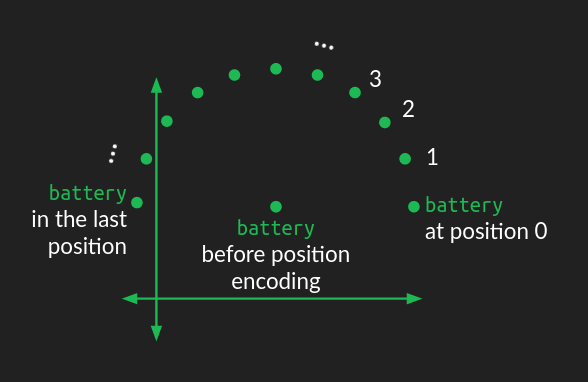
임베딩 공간에서 단어의 위치가 원의 중심이 된다. 여기에 시퀀스에서의 순서에 따라 섭동을 더한다. 각 위치마다 단어가 같은 거리만큼, 하지만 다른 각도로 이동해, 시퀀스를 따라가면 원형 패턴이 된다. 시퀀스에서 서로 가까운 단어들은 비슷한 섭동을, 멀리 떨어진 단어들은 서로 다른 방향의 섭동을 받는다.
원은 2차원 도형이므로, 원형 흔들림을 표현하려면 임베딩 공간의 두 차원을 수정해야 한다. 임베딩 공간이 두 차원보다 크다면(대부분 그렇다), 이 원형 흔들림을 다른 차원 쌍들에도 반복 적용하되, 각기 다른 각주파수(회전 수)로 적용한다. 어떤 차원쌍에서는 여러 바퀴를 돌고, 다른 차원쌍에서는 한 바퀴의 일부분만 돈다. 다양한 주파수의 원형 흔들림을 합치면, 시퀀스 내에서 단어의 절대 위치를 잘 나타낼 수 있다.
개인적으로 왜 이게 잘 작동하는지에 대한 직관은 아직 개발 중이다. 어휘 간 학습된 관계와 어텐션을 깨뜨리지 않으면서 위치 정보를 섞어 넣는 방법인 듯하다. 수학과 함의를 더 깊이 파고들고 싶다면 Amirhossein Kazemnejad의 위치 인코딩 튜토리얼을 추천한다.
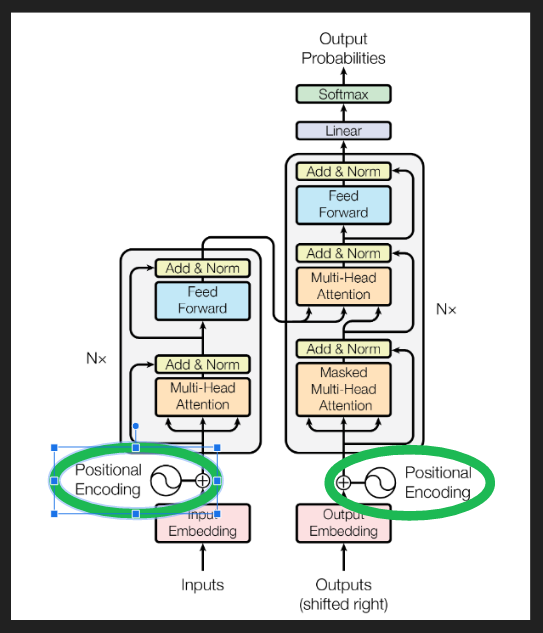
표준 아키텍처 다이어그램에서 아래 블록이 위치 코드 생성과 임베딩에의 더하기를 보여준다.
임베딩은 단어를 다루기 훨씬 효율적으로 만들어 준다. 하지만 파티가 끝나면, 다시 원래 어휘의 단어로 되돌려야 한다. 디임베딩(de-embedding)은 임베딩과 같은 방식, 즉 한 공간에서 다른 공간으로의 투영(행렬 곱)으로 한다.
디임베딩 행렬의 모양은 임베딩 행렬과 같지만, 행과 열이 뒤바뀐다. 행 개수는 변환 ‘출발’ 공간의 차원이다. 예시에서는 임베딩 공간의 크기인 2다. 열 개수는 변환 ‘도착’ 공간의 차원—원-핫 어휘 공간의 크기, 예시에서는 13—이다.
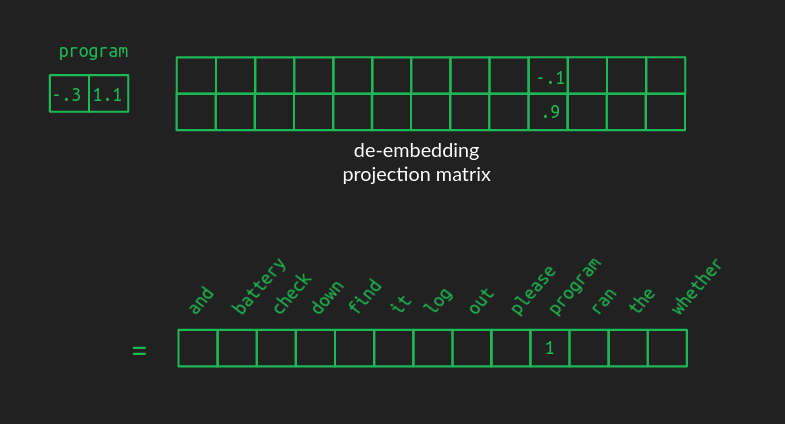
좋은 디임베딩 행렬의 값은 임베딩 행렬만큼 직관적으로 그려지지 않지만, 효과는 비슷하다. 예를 들어 _program_을 나타내는 임베딩 벡터에 디임베딩 행렬을 곱하면, 해당 위치의 값이 크다. 하지만 고차원 공간으로의 투영 특성상 다른 단어들의 값이 0이 되지는 않는다. 임베딩 공간에서 _program_에 가까운 단어들도 중간 정도의 큰 값을 갖는다. 다른 단어들은 거의 0일 것이다. 음수 값도 많이 생길 가능성이 높다. 어휘 공간의 결과 벡터는 더 이상 원-핫이나 희소(sparse)하지 않다. 거의 모든 값이 0이 아닌 밀집(dense) 벡터다.
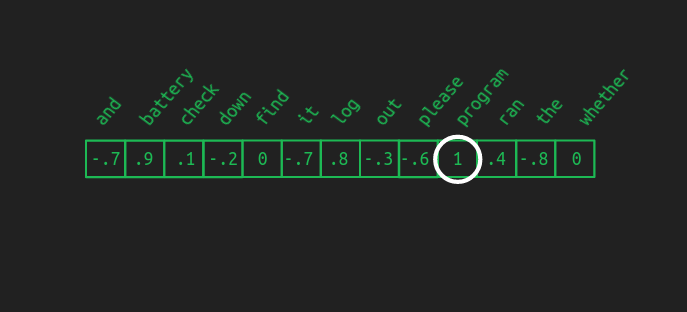
괜찮다. 가장 큰 값을 가진 단어를 선택해 원-핫 벡터를 ‘다시 만들’ 수 있다. 이를 argmax라고도 한다. 최대값을 주는 원소(인덱스)를 고르는 연산이다. 위에서 말한 그리디 시퀀스 완성의 방식이다. 훌륭한 1차 시도지만, 더 나은 것도 있다.
어떤 임베딩이 여러 단어에 비슷하게 잘 매핑되면, 매번 최고만 고르지 않는 편이 나을 수 있다. 아주 조금 더 나은 정도라면 다양성을 조금 추가해 결과를 더 흥미롭게 만들 수 있다. 또한 때로는 몇 단어를 앞서 내다보고, 문장이 어떤 방향으로 갈 수 있는지 여러 갈래를 고려한 뒤에 최종 선택을 하는 것도 유용하다. 이를 위해서는 우선 디임베딩 결과를 확률분포로 바꿔야 한다.
argmax는 ‘하드’하다. 최고값이 다른 값보다 아무리 미세하게만 커도 승자다. 여러 가능성을 동시에 품고 싶다면 ‘소프트’한 최대 함수, **소프트맥스(softmax)**가 낫다. 벡터의 값 x에 대한 소프트맥스는 e^x를 벡터의 모든 값에 대한 지수들의 합으로 나눈 값이다.
소프트맥스는 여기서 세 가지로 유용하다. 첫째, 디임베딩 결과 벡터를 임의의 숫자 모음에서 ‘확률분포’로 바꿔 준다. 확률이 되면, 서로 다른 단어가 선택될 가능성을 비교하기 쉬워지고, 더 나아가 앞에 몇 단어를 보고 여러 방향의 문장 전개를 동시에 고려할 수 있다.
둘째, 상단의 후보를 ‘얇게’ 만든다. 한 단어가 다른 것들보다 확연히 높게 나오면, 소프트맥스는 그 차이를 과장해서 argmax처럼 보이게 한다. 승자가 1에 가깝고, 나머지가 0에 가깝다. 하지만 상위권에 비슷비슷한 후보가 여럿 있으면, 소프트맥스는 그들을 ‘높은 확률’로 모두 보존한다. 아슬아슬한 2등들을 인위적으로 압착해 죽이지 않는다.
셋째, 소프트맥스는 미분 가능하다. 즉, 입력의 어떤 원소를 조금 바꿨을 때 출력의 각 원소가 얼마나 변하는지 계산할 수 있다. 덕분에 역전파로 트랜스포머를 학습시킬 수 있다.
소프트맥스를 제대로 이해하고 싶다면(혹은 잠이 안 온다면) 좀 더 자세한 글을 추천한다.
디임베딩 변환(아래 다이어그램의 Linear 블록)과 소프트맥스를 합치면 디임베딩 과정이 완성된다.
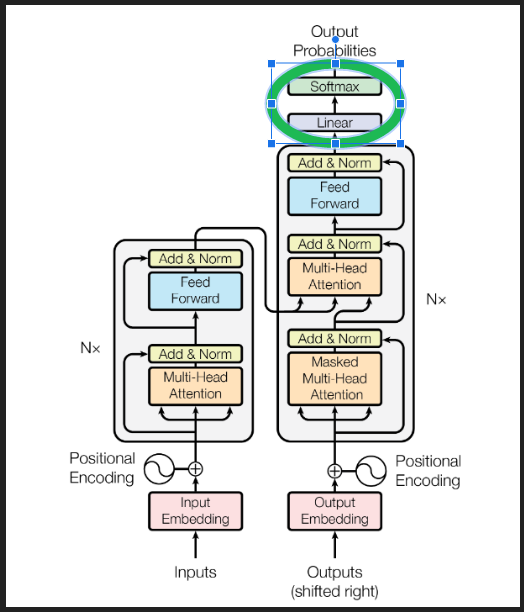
이제 투영(행렬 곱)과 공간(벡터 크기) 개념에 익숙해졌으니, 핵심 어텐션 메커니즘을 다시 보자. 각 단계에서 행렬의 모양을 좀 더 구체적으로 말할 수 있으면 이해에 도움이 된다. 중요한 숫자는 다음과 같다.
원래 입력 행렬은 문장 내 단어를 원-핫으로 만든 뒤, 각 원-핫 벡터를 행으로 쌓아서 만든다. 결과 입력 행렬의 모양은 [n x N]이다.
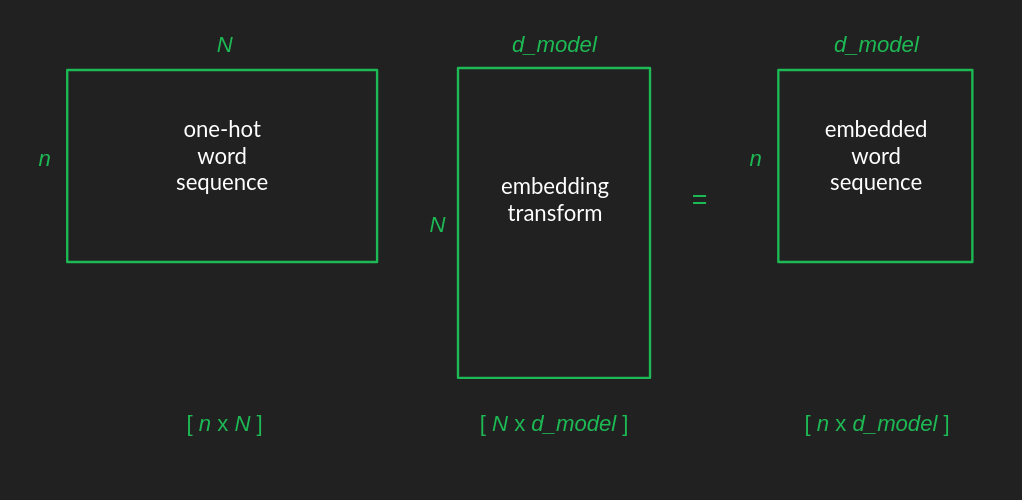
임베딩 행렬은 [N x d_model]이다. 두 행렬을 곱하면, 결과의 행 수는 첫 번째 행렬에서, 열 수는 두 번째 행렬에서 온다. 따라서 임베딩된 단어 시퀀스 행렬의 모양은 [n x d_model]이다.
트랜스포머 전반을 따라 행렬 모양의 변화를 추적하면 이해에 도움이 된다. 초기 임베딩 이후, 위치 인코딩은 더하기(가산)라서 모양을 바꾸지 않는다. 그 다음 임베딩된 시퀀스가 어텐션 층으로 들어가고, 나올 때도 모양은 같다(곧 내부로 들어간다). 마지막에 디임베딩이 원래 모양으로 되돌리고, 시퀀스의 각 위치마다 어휘 전체에 대한 확률을 제공한다.
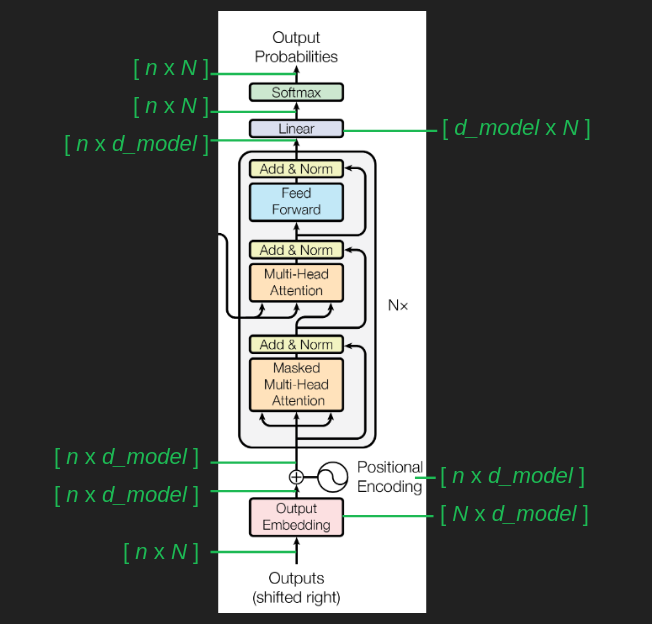
이제 앞서 단순화했던 가정을 정면으로 다룰 시간이다. 단어는 원-핫이 아니라 ‘밀집’ 임베딩 벡터로 표현된다. 어텐션은 1이나 0, 켜짐/꺼짐만 있는 것이 아니라 그 사이 어디든 될 수 있다. 값을 0과 1 사이로 만들기 위해 소프트맥스를 다시 쓴다. 값들을 [0, 1] 범위로 밀어 넣을 뿐 아니라, 가장 큰 값을 강조하고 작은 값을 적극적으로 누른다. 최종 출력 해석에서 썼던 ‘미분 가능한 거의-argmax’와 같은 역할이다.
하지만 어텐션에 소프트맥스를 넣으면 한 가지 복잡해진다. 한 요소에 초점을 맞추는 경향이 생긴다. 이전에는 없던 제한이다. 때로는 다음을 예측할 때 앞선 단어 여러 개를 동시에 ‘기억’하는 것이 유용한데, 소프트맥스가 이를 앗아간다. 모델에는 문제가 된다.
해결책은 어텐션을 여러 인스턴스, 즉 **헤드(head)**로 동시에 돌리는 것이다. 그러면 트랜스포머가 여러 이전 단어를 동시에 고려할 수 있다. 소프트맥스를 끌어들여 잃었던 힘을 되찾는다.
안타깝게도 계산량이 크게 늘어난다. 어텐션 계산이 이미 비용의 대부분이었는데, 원하는 헤드 수만큼 곱해 버렸다. 이를 피하려면, 다시 ‘더 낮은 차원의 임베딩 공간으로 투영’하는 트릭을 쓴다. 행렬 크기를 줄여 계산 시간을 극적으로 줄인다. 상황이 구원된다.
이를 추적하려면, 멀티헤드 어텐션 블록의 분기와 합류를 따라가며 행렬 모양을 더 보자. 숫자는 세 가지가 더 필요하다.
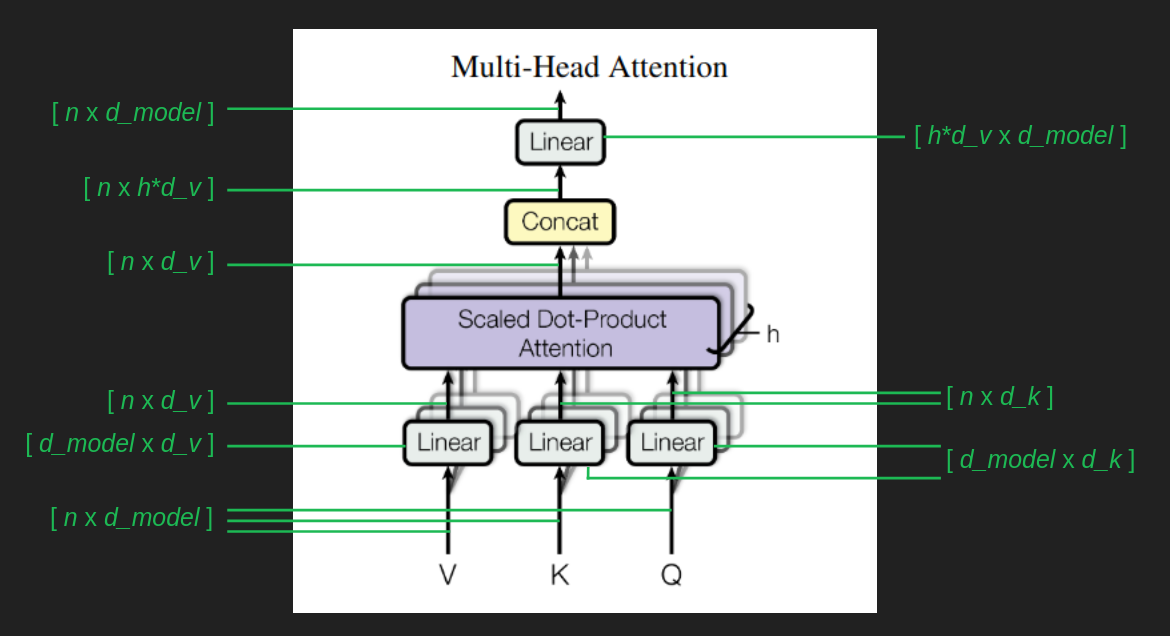
[n x d_model]인 임베딩된 단어 시퀀스가 모든 것의 기반이다. 각 경우마다, Wv, Wq, _Wk_라는 행렬(아키텍처 다이어그램에서는 모두 ‘Linear’로 표시된)이 원래 임베딩된 시퀀스를 변환해 값 행렬 V, 쿼리 행렬 Q, 키 행렬 _K_를 만든다. _K_와 _Q_는 [n x d_k]로 같은 모양이고, _V_는 [n x d_v]처럼 다를 수 있다. 논문에서는 d_k와 d_v가 같지만, 반드시 그럴 필요는 없다. 중요한 점은, 각 어텐션 헤드가 고유한 Wv, Wq, Wk 변환을 가진다는 것이다. 즉, 각 헤드가 임베딩 공간에서 자신이 보고 싶은 부분을 확대/축소해서 집중할 수 있고, 다른 헤드와 다를 수 있다.
각 헤드의 어텐션 결과의 모양은 _V_와 같다. 이제 서로 다른 요소에 주의를 둔 h개의 결과 벡터가 있다. 이를 하나로 합치려면, 선형대수의 힘을 빌려 이 결과들을 열 방향으로 이어붙여 [n x (hd_v)]로 만들고, 다시 [hd_v x d_model] 변환으로 원래 모양으로 되돌린다.
간단히 쓰면 아래와 같다.
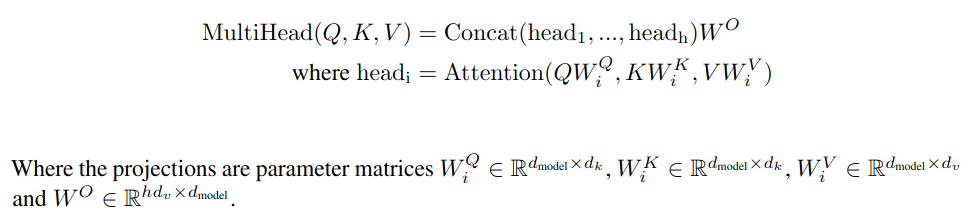
우리는 이미 위에서 어텐션의 개념적 그림을 걸었다. 실제 구현은 조금 더 지저분하지만, 그때의 직관이 여전히 도움이 된다. 쿼리와 키는 이제 각기 제멋대로의 하위 임베딩 공간으로 투영되어 직접 들여다보고 해석하기 어렵다. 개념도의 경우, 쿼리 행렬의 한 행은 어휘 공간의 한 점이고(원-핫 덕분에 정확히 하나의 단어에 해당), 키 모음과의 매핑으로 어떤 값들을 통과시키는지를 거른다. 실제 구현에서는 각 어텐션 헤드가 쿼리 단어를 또 다른 저차원 임베딩 공간의 한 점으로 보낸다. 그 결과 어텐션은 ‘개별 단어’ 사이가 아니라 ‘단어 그룹’ 사이의 관계가 된다. 임베딩 공간의 의미론적 근접성을 활용해, 비슷한 단어들에 대해 배운 것을 일반화한다.
계산을 따라가며 행렬 모양을 보면 이해에 도움이 된다.
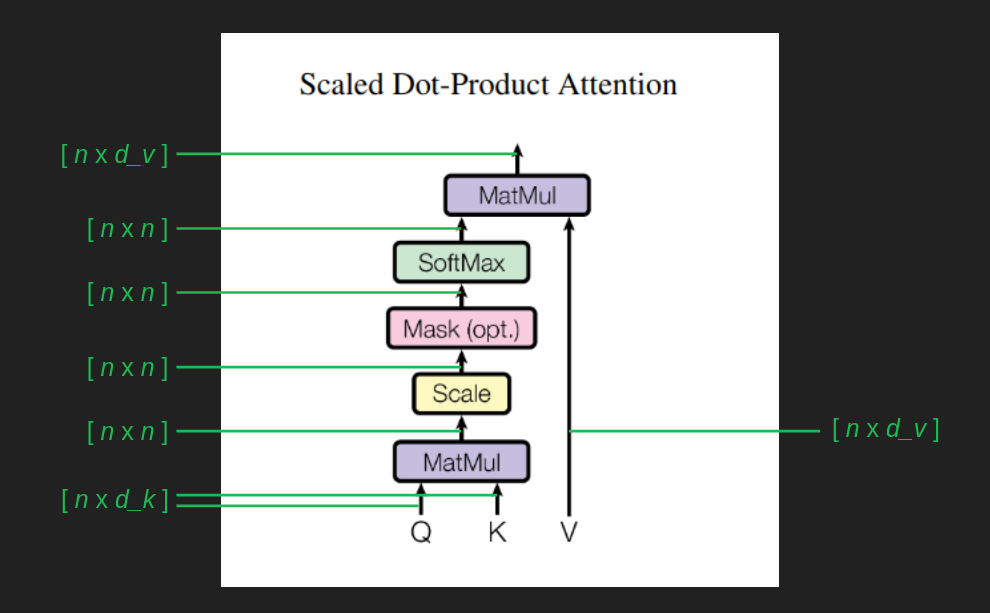
_Q_와 _K_는 [n x d_k]다. _K_를 전치한 뒤 곱하므로 _QK^T_의 결과는 [n x d_k] * [d_k x n] = [n x n]이 된다. 이 행렬의 모든 원소를 sqrt(d_k)로 나누면 값의 크기가 마구 커지는 것을 막고 역전파가 잘 작동하도록 돕는 것으로 알려져 있다. 소프트맥스는 앞서 말했듯 거의-argmax로 값을 깎아, 시퀀스의 한 요소에 초점을 맞추는 경향을 만든다. 이렇게 [n x n] 어텐션 행렬은, 대략, 시퀀스의 각 요소를 시퀀스의 다른 요소 하나(또는 소수)로 매핑해, ‘다음을 예측할 때 어떤 요소를 바라봐야 가장 유용한지’를 표시한다. 마지막으로 값 행렬 _V_에 이 필터를 적용해, 주목된 값만 남긴다. 시퀀스에서 대부분의 과거를 무시하고 ‘가장 유용한’ 하나에 스포트라이트를 비춘다.
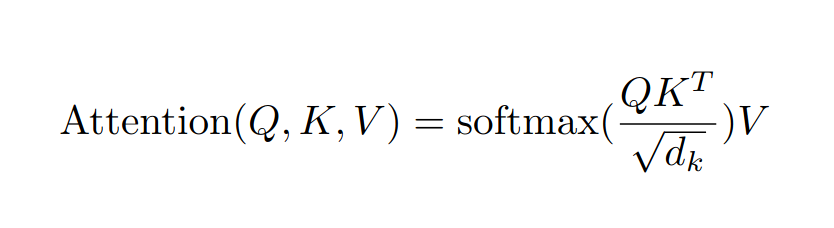
이 계산을 이해하기 어려운 부분 하나는, 입력 시퀀스의 ‘모든 요소’에 대해 어텐션을 계산한다는 점이다. 문장의 모든 단어에 대해, ‘가장 최근’뿐 아니라 그 이전의 단어들에 대해서도 계산한다. 우리가 정말로 관심 있는 것은 이미 예측되어 확정된 단어들의 다음 단어가 아니므로, 그들의 계산은 덜 중요하다. 아직 오지 않은 ‘미래 단어’들에 대해서도 계산한다. 이들은 아직 쓸모가 적다. 그들의 직전 단어마저 정해지지 않았기 때문이다. 하지만 간접 경로를 통해 가장 최근 단어의 어텐션에 영향을 미칠 수 있으므로 모두 포함한다. 마지막에 시퀀스의 각 위치에 대한 단어 확률을 계산할 때, 우리는 대부분을 버리고 ‘다음 단어’만 본다.
Mask 블록은 적어도 시퀀스 완성 과제에서는 ‘미래를 보면 안 된다’는 제약을 강제한다. 가상의 미래 단어에서 이상한 아티팩트가 들어오는 것을 막는다. 방법은 투박하지만 효과적이다. 현재 위치를 지난 단어들에 대한 어텐션은 모두 -무한대로 설정한다. The Annotated Transformer라는, 논문의 파이썬 구현을 줄줄이 보여주는 더없이 유익한 동반 글에서는 마스크 행렬을 시각화한다. 보라색 셀은 어텐션이 금지된 곳이다. 각 행은 시퀀스의 한 요소에 대응한다. 첫 행은 자기 자신(첫 요소)만 볼 수 있고, 그 이후는 못 본다. 마지막 행은 자기 자신(마지막 요소)과 그 이전의 모든 것을 볼 수 있다. 마스크는 [n x n] 행렬이다. 행렬 곱이 아니라, 더 직접적인 원소별 곱으로 적용한다. 이는 어텐션 행렬의 보라색 위치들을 직접 -무한대로 설정하는 효과를 낸다.
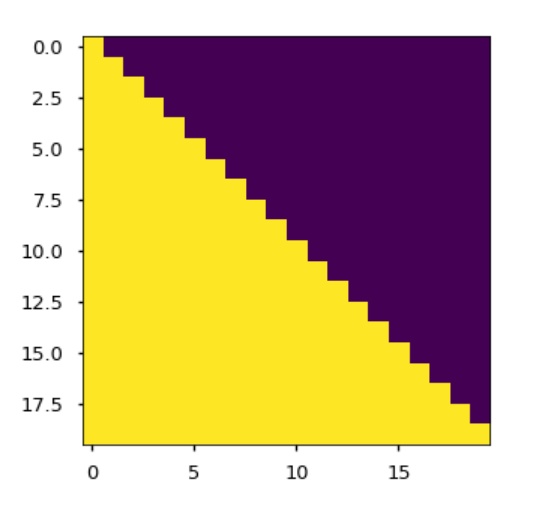
어텐션 구현의 또 다른 중요한 차이는, 단어-단어 관계가 아니라 ‘위치-위치’ 관계를 표현한다는 점이다. 이는 [n x n] 모양에서 분명하다. 행 인덱스로 시퀀스의 한 요소를, 열 인덱스로 다른 요소(들)를 가리킨다. 임베딩 공간에서 동작하기 때문에, 우리가 추가로 ‘임베딩 공간의 이웃 단어’를 찾아 관계를 해석하는 수고를 덜고, 그냥 위치 관계를 바로 시각화하고 해석할 수 있게 한다.
어텐션은 트랜스포머가 하는 일의 가장 근본적인 부분이다. 핵심 메커니즘이며, 이제 우리는 꽤 구체적인 수준까지 따라왔다. 여기서부터는 잘 돌아가게 만드는 배관(plumbing)이다. 무거운 짐을 끄는 마구(하네스)에서 어텐션이 힘을 쓰도록 돕는 나머지다.
아직 설명하지 않은 한 조각은 스킵 연결(skip connection)이다. 이는 멀티헤드 어텐션 블록과, 원소별 피드포워드 블록 주위의 "Add and Norm" 레이블 블록에 있다. 스킵 연결에서는 입력의 사본을 계산 결과에 더한다. 어텐션 블록의 입력은 그 출력에 더해지고, 원소별 피드포워드 블록의 입력도 그 출력에 더해진다.
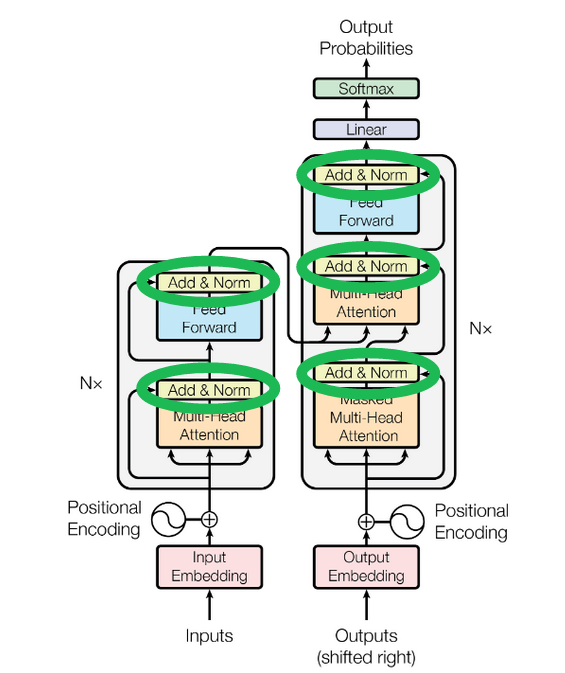
스킵 연결은 두 가지 목적을 가진다.
첫째, 그래디언트를 매끄럽게 유지하는 데 도움이 된다. 이는 역전파에 큰 도움이다. 어텐션은 필터다. 잘 작동하면 대부분을 걸러낸다. 그 결과, 많은 입력의 작은 변화가, 막혀 있는 채널에 해당한다면, 출력의 변화를 거의 만들지 못한다. 이는 계곡 바닥도 아닌데 평평한 ‘죽은 지점’을 만든다. 이런 안장점(saddle)과 능선(ridge)은 역전파의 큰 걸림돌이다. 스킵 연결은 이를 완화한다. 극단적으로, 모든 가중치가 0이어서 모든 입력이 막혀도, 스킵 연결이 입력 사본을 결과에 더해, 어떤 입력의 작은 변화도 결과에 감지 가능한 변화를 보장한다. 그래디언트 하강이 좋은 해에서 멀리 떨어진 곳에서 멈춰 서는 것을 막는다.
스킵 연결은 ResNet 이미지 분류기 시대부터 성능 개선으로 인기를 얻었고, 이제 신경망 아키텍처의 표준 기능이다. 시각적으로도 스킵 연결의 효과를 볼 수 있다. 다음 논문의 그림은 스킵 연결이 있는 ResNet과 없는 ResNet의 비교다. 손실 함수 표면의 경사들이 스킵 연결을 쓰면 훨씬 온건하고 균일하다. 더 깊이 파고들고 싶다면 이 글을 추천한다.
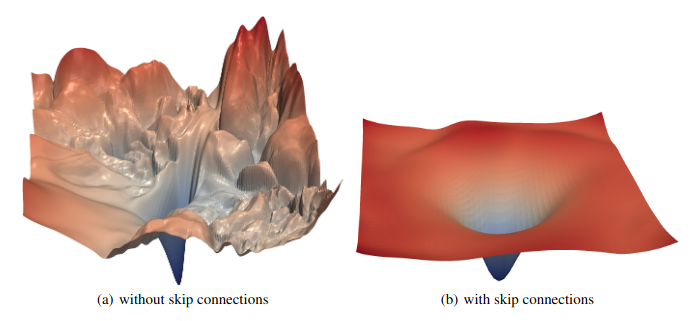
둘째, 트랜스포머에 특화된 목적—원래 입력 시퀀스의 보존이다. 헤드가 많아도, 단어가 자기 자신의 위치에 주목한다는 보장은 없다. 어텐션 필터가 가장 최근 단어를 완전히 잊고, 관련 있어 보이는 앞선 단어들만 바라볼 수도 있다. 스킵 연결은 원래의 단어를 신호에 ‘수동으로’ 더해, 빠뜨리거나 잊어버릴 수 없게 한다. 이런 강건성은 트랜스포머가 다양한 시퀀스 완성 과제에서 좋은 행동을 보이는 이유 중 하나일 수 있다.
정규화(normalization)는 스킵 연결과 잘 어울리는 단계다. 반드시 같이 있어야 하는 것은 아니지만, 어텐션이나 피드포워드 신경망처럼 계산 묶음 뒤에 둘 때 가장 좋은 효과를 낸다.
레이어 정규화의 짧은 설명은, 행렬의 값을 평균 0, 표준편차 1이 되도록 이동하고 스케일링하는 것이다.
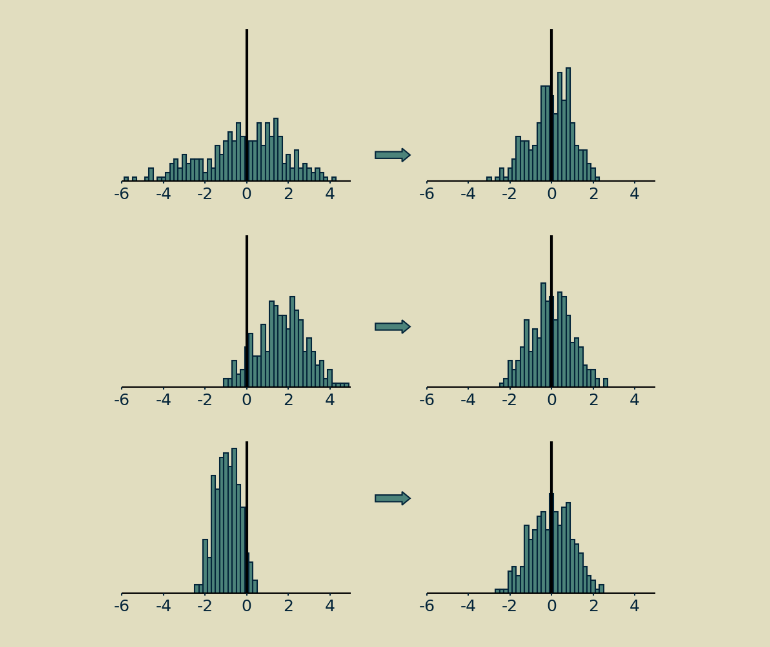
긴 설명은 이렇다. 트랜스포머처럼 움직이는 조각이 많고, 그중 일부가 행렬 곱이 아닌(소프트맥스, ReLU 같은) 시스템에서는, 값의 크기와 양/음의 균형이 중요하다. 모든 것이 선형이라면 입력을 두 배로 하면 출력도 두 배가 되어 문제가 없다. 신경망은 그렇지 않다. 본질적으로 비선형이라 매우 표현력이 좋지만, 신호의 크기와 분포에 민감하다. 정규화는 다층 신경망 전반에서 각 단계의 신호 분포를 일정하게 유지하는 데 유용한 기법으로 입증되었다. 파라미터 수렴을 돕고 대체로 더 나은 성능으로 이어진다.
정규화에 대해 내가 가장 좋아하는 점은, 이런 높은 수준의 설명을 제외하면 ‘왜 그렇게 잘 작동하는지’ 아무도 완전히 확신하지 않는다는 사실이다. 이 토끼굴을 더 내려가 보고 싶다면, 트랜스포머에서 쓰는 레이어 정규화의 사촌격인 배치 정규화에 대해 내가 쓴 좀 더 자세한 글이 있다.
앞서 토대를 놓으며, ‘어텐션 블록 하나 + 피드포워드 블록 하나에 알맞은 가중치’를 주면 적당한 언어 모델이 된다는 것을 보였다. 예시에서는 대부분의 가중치가 0, 몇 개가 1이었고, 손으로 골랐다. 원시 데이터에서 학습할 때는 이런 호사를 누리지 못한다. 처음에는 가중치가 모두 랜덤으로 선택되고, 대부분 0에 가깝고, 0이 아닌 소수도 정작 필요한 값과 다를 가능성이 높다. 모델이 잘 동작하기까지 갈 길이 멀다.
역전파를 통한 확률적 경사 하강(SGD)은 놀라운 일을 해낼 수 있지만, 운에 크게 의존한다. 좋은 답으로 가는 길이 하나뿐이고, 올바른 가중치 조합이 단 하나뿐이라면, 거기에 도달할 확률은 낮다. 하지만 좋은 해로 가는 경로가 많다면 도달 확률은 훨씬 커진다.
어텐션 층이 하나뿐이면(멀티헤드 어텐션 블록 하나 + 피드포워드 블록 하나), 트랜스포머 파라미터를 잘 맞추는 경로가 하나뿐이다. 모든 행렬의 모든 원소가 올바른 값으로 수렴해야 한다. 연약하고 부서지기 쉽다. 초기 추정이 매우 운 좋지 않다면, 한참 나쁜 해에 갇히기 쉽다.
트랜스포머가 이를 피하는 방법은 다층 어텐션이다. 각 층은 이전 층의 출력을 입력으로 받는다. 스킵 연결 덕분에 파이프라인 전체가 개별 어텐션 블록의 실패나 이상한 결과에 강건하다. 여러 층이 있다는 것은 다른 층들이 기다리고 있다는 뜻이다. 하나가 탈선하거나 잠재력을 발휘하지 못해도, 뒤에 있는 다른 층이 빈틈을 메우거나 오류를 고칠 기회를 또 갖는다. 논문은 층이 많을수록 성능이 좋아졌지만, 6층 이후에는 개선이 점차 작아졌다고 보고한다.
다층 구조를 다른 방식으로 생각하면 ‘컨베이어벨트 조립라인’이다. 각 어텐션 블록과 피드포워드 블록은 입력을 라인에서 끌어내 계산하고, 유용한 어텐션 행렬을 만들고, 다음 단어 예측을 한다. 무엇을 만들든, 유용하든 아니든, 결과를 다시 컨베이어에 올리고 다음 층으로 넘긴다.
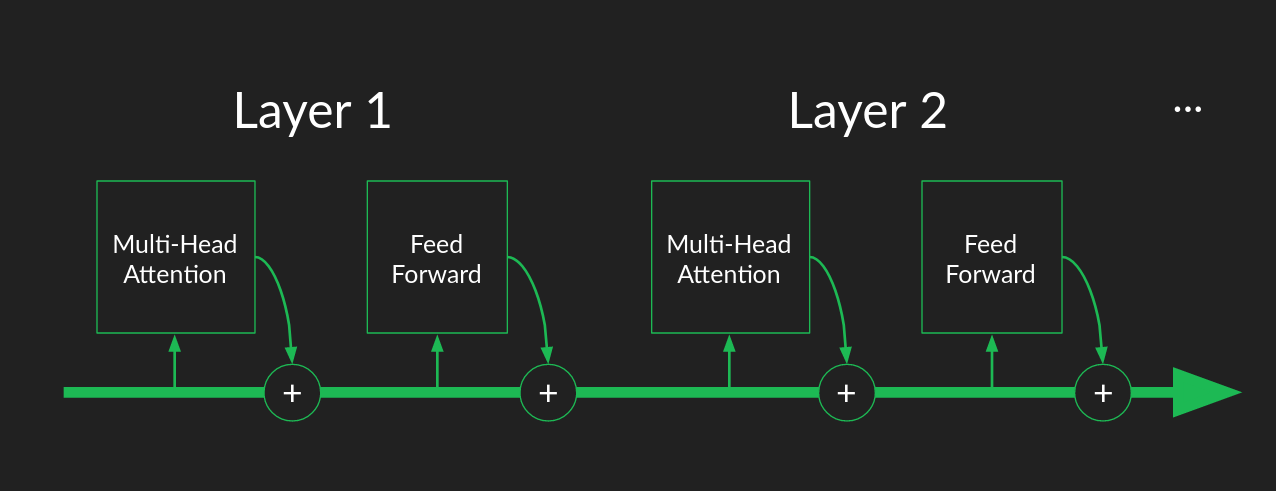
이는 전통적으로 다층 신경망을 ‘깊다’로 묘사하는 것과 다르다. 스킵 연결 덕분에, 연속된 층이 점점 정교한 추상화를 만든다기보다 ‘중복성’을 제공한다. 한 층에서 주의를 맞추고 유용한 피처를 만들고 정확한 예측을 할 기회를 놓쳐도, 다음 층이 잡아준다. 층들은 조립라인의 작업자처럼, 각자 할 수 있는 일을 하지만 모든 조각을 잡아내지 못해도 괜찮다. 다음 작업자가 놓친 것을 잡을 것이다.
지금까지는 인코더 스택(아키텍처의 왼쪽)을 조심스레 무시하고, 디코더 스택(오른쪽)에 집중했다. 곧 고치겠지만, 디코더만으로도 아주 유용하다는 점을 짚을 가치가 있다.
시퀀스 완성에서 설명했듯, 디코더는 부분 시퀀스를 완성하고 원하는 만큼 길게 늘일 수 있다. OpenAI는 생성 사전학습(GPT) 모델군을 바로 이 목적을 위해 만들었다. 그들이 이 리포트에서 설명한 아키텍처는 익숙할 것이다. 인코더 스택과 그 연결을 외과적으로 제거한 트랜스포머다. 남는 것은 12층 디코더 스택이다.
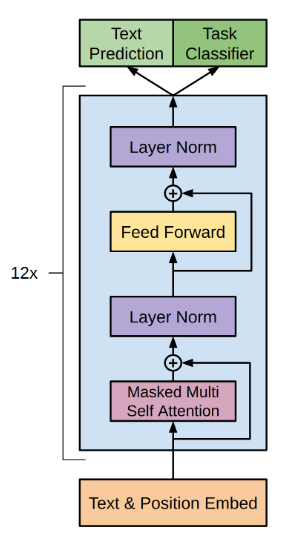
BERT, ELMo, Copilot 같은 생성 모델을 볼 때마다, 트랜스포머의 디코더 절반이 작동하고 있다고 생각해도 대체로 맞다.
디코더에 대해 배운 거의 모든 것이 인코더에도 적용된다. 가장 큰 차이는 마지막에 ‘정오판단’에 쓰일 명시적 예측이 없다는 점이다. 인코더 스택의 산출물은 다소 추상적이다—임베딩 공간의 벡터 시퀀스. 이를 특정 언어나 어휘와 분리된 ‘순수한 의미 표현’이라고 묘사하기도 하지만, 내 귀에는 다소 낭만적으로 들린다. 확실한 것은, 디코더 스택에 ‘의도와 의미’를 전달하는 데 유용한 신호라는 점이다.
인코더 스택이 있으면 트랜스포머의 잠재력이 완전히 열린다. 단순 생성뿐 아니라 한 언어에서 다른 언어로 ‘변환(번역)’할 수 있다. 번역 과제는 시퀀스 완성과는 훈련이 다르다. 학습 데이터에 원어 시퀀스와 목표 언어 시퀀스의 쌍이 필요하다. 원어 전체를 인코더로 통과시킨다(이번에는 마스킹이 없다. 번역을 만들기 전에 전체 문장을 볼 수 있다고 가정하기 때문이다). 마지막 인코더 층의 출력이 각 디코더 층의 입력으로 제공된다. 그런 다음 디코더에서는 프롬프트 없이도 앞서처럼 시퀀스 생성이 진행된다.
마지막으로 풀 트랜스포머를 완성하는 조각은 인코더와 디코더 스택 사이의 연결, 크로스 어텐션 블록이다. 마지막으로 남겼지만, 지금까지의 토대로 설명할 것은 많지 않다.
크로스 어텐션은 셀프 어텐션과 거의 같다. 차이는 키 행렬 _K_와 값 행렬 _V_가 이전 디코더 층의 출력이 아니라, ‘마지막 인코더 층의 출력’에 기반한다는 점뿐이다. 쿼리 행렬 _Q_는 여전히 이전 디코더 층의 결과에서 계산된다. 이것이 소스 시퀀스의 정보가 타깃 시퀀스로 흘러들어가 생성 과정을 올바른 방향으로 이끄는 채널이다. 흥미로운 점은, 같은 ‘임베딩된 소스 시퀀스’가 모든 디코더 층에 제공된다는 것이다. 이는 연속된 층이 ‘중복성’을 제공하며 같은 과제를 협력해 수행한다는 생각을 뒷받침한다.
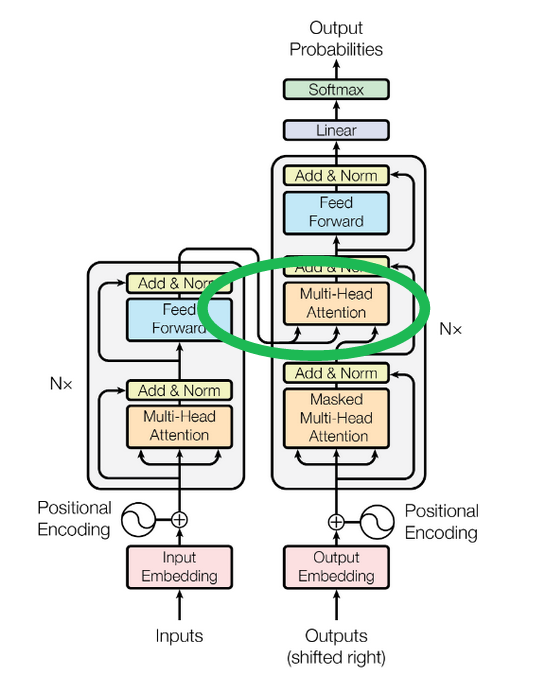
여기까지 트랜스포머를 완주했다! 더 이상 신비한 블랙박스는 없어야 한다. 몇 가지 구현 세부는 파지 않았다. 직접 작동하는 버전을 만들려면 알아야 할 것들이다. 이 마지막 몇 조각은 트랜스포머가 ‘어떻게 작동하는가’보다는, 신경망이 ‘잘 행동하도록’ 만드는 법에 가깝다. The Annotated Transformer가 빈틈을 메워 줄 것이다.
아직 완전히 끝난 것은 아니다. 데이터를 처음에 어떻게 표현할지에 대해 말할 것이 남았다. 내게 가까운 주제지만 소홀히 하기 쉽다. 알고리즘의 힘보다는, 데이터를 사려 깊게 해석하고 그 의미를 이해하는 일에 가깝다.
앞서 어휘를 고차원 원-핫 벡터로 표현할 수 있다고 슬쩍 말했다. 그러려면 몇 개의 단어를 어떤 단어로 표현할지 정확히 알아야 한다.
순진한 접근은 모든 가능한 단어 목록을 만드는 것이다. 웹스터 사전 같은 곳에서 찾을 수 있는 목록처럼. 영어에서는 수만 단어가 될 것이고, 포함/제외 기준에 따라 정확한 숫자는 달라질 것이다. 하지만 이는 과도한 단순화다. 대부분의 단어는 복수형, 소유격, 활용형 등 여러 형태를 갖는다. 이형 철자도 있을 수 있다. 데이터가 아주 깔끔히 정제되지 않았다면 온갖 오타도 들어 있을 것이다. 자유형 텍스트, 신조어, 속어, 전문용어, 유니코드의 거대한 우주까지 생각하면, 모든 가능한 단어의 완전 목록은 비현실적으로 길다.
합리적인 차선책은 단어 대신 개별 문자(character)를 구성요소로 삼는 것이다. 문자의 완전 목록은 계산 용량 안에 충분히 들어온다. 하지만 문제가 두 가지 있다. 데이터를 임베딩 공간으로 바꾸고 나면, 우리는 그 공간의 ‘거리’가 의미론적이라고 가정한다. 즉, 가까운 점은 비슷한 의미, 먼 점은 매우 다른 의미라고 가정한다. 그래서 어떤 단어에 대해 배운 것을 그 이웃들에게 암묵적으로 확장하고, 이는 계산 효율과 일반화 능력의 원천이 된다.
문자 수준에서는 의미론이 거의 없다. 영어에도 한 글자짜리 단어가 있지만 많지 않다. 이모지는 예외지만, 대부분의 데이터셋의 주요 내용은 아니다. 즉, 임베딩 공간이 ‘쓸모없게’ 된다.
이론적으로는, 충분히 풍부한 문자 조합을 보아 ‘단어’나 ‘어간’, ‘단어쌍’ 같은 의미 있는 시퀀스를 만들 수 있다면 우회할 수 있을지도 모른다. 하지만 트랜스포머가 내부에서 만드는 피처는 ‘순서가 있는 입력 집합’이라기보다 ‘입력 쌍의 모음’에 가깝게 행동한다. 즉, ‘단어의 표현’이 문자쌍의 모음이 되고, 순서가 강하게 표현되지 않는다. 결국 항상 애너그램들을 다루게 되어 일이 훨씬 어려워진다. 실제로 문자 수준 표현으로는 트랜스포머가 잘 동작하지 않는다는 실험 결과가 있다.
다행히 우아한 해법이 있다. 바이트 쌍 인코딩(Byte Pair Encoding, BPE)이다. 문자 수준 표현에서 시작해 각 문자에 고유 바이트(코드)를 준다. 대표 데이터 일부를 훑은 뒤, 가장 흔한 바이트 ‘쌍’을 묶어 새 바이트(새 코드)를 만든다. 이 새 코드를 데이터에 다시 치환한다. 이 과정을 반복한다.
문자 한 쌍을 나타내는 코드는 다른 문자나 문자쌍 코드와 결합되어 더 긴 시퀀스를 나타내는 새 코드를 만든다. 코드가 나타낼 수 있는 문자 시퀀스 길이에는 제한이 없다. 자주 반복되는 시퀀스를 표현하기에 충분히 길어질 것이다. BPE의 멋진 점은 ‘모든 가능한 시퀀스를 멍청하게 표현하는’ 대신, 데이터에서 ‘어떤 긴 시퀀스를 학습할지’를 추론한다는 것이다. transformer 같은 긴 단어를 하나의 바이트 코드로 배우지만, ksowjmckder 같은 임의 문자열에는 코드를 낭비하지 않는다. 그리고 단일 문자 빌딩 블록에 대한 코드도 모두 유지하므로, 이상한 오타나 신조어, 심지어 외국어도 여전히 표현할 수 있다.
BPE를 쓸 때 우리는 어휘 크기를 정한다. 그 크기에 도달할 때까지 새 코드를 계속 만든다. 어휘 크기는 문자 스트링이 ‘텍스트의 의미를 담을 만큼’ 충분히 길어지도록 클 필요가 있다. 그래야 트랜스포머를 돌릴 만큼 풍부해진다.
BPE를 학습하거나 빌려온 뒤에는, 트랜스포머에 넣기 전에 데이터를 전처리하는 데 쓸 수 있다. 연속된 텍스트를 구분되는 조각(대부분은 알아볼 수 있는 단어이길 바란다)의 시퀀스로 나누고, 각 조각에 간결한 코드를 부여한다. 이것이 토큰화(tokenization)다.
이제 처음으로 돌아가 보자. 우리가 처음 세운 목표는 ‘음성 명령의 오디오 신호를 텍스트로 번역’하는 것이었다. 지금까지의 예시는 문자와 단어를 가정했다. 오디오로 확장할 수 있지만, 더 대담한 신호 전처리가 필요하다.
오디오 신호의 정보는 우리의 귀와 뇌가 말을 이해하는 데 쓰는 부분을 뽑아내는 고급 전처리로 이득을 본다. 방법은 ‘멜 주파수 켑스트럼(MFCC) 필터링’이고, 이름만큼이나 바로크하다. 흥미진진한 세부를 파고들고 싶다면 잘 그림이 붙은 튜토리얼을 추천한다.
전처리가 끝나면, 원시 오디오는 ‘벡터의 시퀀스’로 바뀐다. 각 원소는 특정 주파수 대역의 오디오 활동 변화를 나타낸다. 밀집(dense)하며(0이 없다), 모든 원소는 실수 값이다.
좋은 점은, 각 벡터가 트랜스포머의 ‘단어’(토큰)로 훌륭하다는 것이다. 무언가를 의미한다. 바로 알아들을 수 있는 소리 집합으로 직결된다.
한편, 각 벡터를 단어로 취급하는 것은 이상하다. 모든 벡터가 유일하기 때문이다. 소리가 미묘하게 다른 조합이 너무 많아서 똑같은 벡터 값이 두 번 나타날 확률은 극히 낮다. 앞서 썼던 원-핫이나 BPE 전략은 여기 도움이 되지 않는다.
요령은, 이런 ‘밀집 실수 벡터’는 사실 ‘단어를 임베딩한 뒤’ 우리가 끝내는 형식이라는 점을 알아차리는 것이다. 트랜스포머는 이 형식을 사랑한다. 이를 활용하려면, 켑스트럼 전처리 결과를 ‘텍스트 예시에서의 임베딩된 단어’처럼 쓰면 된다. 토큰화와 임베딩 단계를 생략할 수 있다.
이건 다른 데이터에도 그대로 적용된다. 많은 기록 데이터가 ‘밀집 벡터의 시퀀스’ 형태다. 그런 데이터는 트랜스포머 인코더에, 마치 임베딩된 단어인 것처럼 바로 꽂아 넣을 수 있다.
여기까지 함께 해 준다면, 고맙다. 그만한 가치가 있었길 바란다. 우리의 여정은 여기까지다. 상상의 음성 제어 컴퓨터를 위한 음성-텍스트 변환기를 만드는 목표에서 출발해, 가장 기초적인 빌딩 블록(셈과 산술)에서 시작해 트랜스포머를 바닥부터 재구성했다. 이제 최신 자연어 처리 정복 기사들을 읽을 때, 보닛 아래에서 무슨 일이 벌어지는지 꽤 그럴듯한 정신 모델을 품고 흐뭇하게 고개를 끄덕일 수 있기를.
2021년 10월 29일