Schubfach 알고리즘을 기반으로 한, 약 200줄짜리 C++ 코드로 구현한 고성능 double→문자열 변환(dtoa)의 개념과 최소 구현, 그리고 성능을 설명한다.

부동소수점 수를 그 수의 가장 짧은 10진수 표현으로 변환하는 문제는 오랫동안 놀랄 만큼 까다로운 문제였다. 수십 년 동안 개발자들은 다중 정밀도 연산을 사용하는 Dragon4 같은 알고리즘에 의존해 왔다. 보다 최근에는, Ryu, Schubfach 그리고 Dragonbox와 같은, 수학적으로 정확성이 증명된 고성능 알고리즘의 새로운 세대가 등장했다.
이전 글인 150줄로 구현하는 double→문자열 변환에서는, 올바른 동작을 유지하면서 기본 구현을 얼마나 작게 만들 수 있는지 살펴보았다. Schubfach 알고리즘은 이 아이디어를 훨씬 더 밀어붙인다. 이 알고리즘은, 단순한 알고리즘과 비슷한 분량의 코드로 완전히 증명된(correctness가 증명된) 고성능 dtoa를 구현할 수 있게 해준다. 이 글에서는 Schubfach를 간단히 개관한 뒤, 저장소 https://github.com/vitaut/schubfach에 있는 최소 C++ 구현을 단계별로 살펴본다.
Raffaello Giulietti가 제안한 Schubfach 알고리즘은, 이진 부동소수점 수를 가장 짧고, 올바르게 반올림된, 왕복이 보장되는(round-trip guarantee) 10진수 문자열 표현으로 변환하는 방법이다. 이 알고리즘은 두 가지 핵심 통찰에 기반한다.
이 알고리즘은, 알고리즘 이름의 근원이기도 한 Schubfachprinzip (비둘기집 원리)에 기반하여, 최적의 최단 10진 표현 ()에 대한 올바른 10진 지수()를 효율적으로 결정한다.
최단 10진 표현을 반복적으로 탐색하는 대신, Schubfach는 주어진 스케일()에서 인접한 10진 값들 사이의 거리()와 부동소수점 수의 반올림 구간(rounded interval) 폭()을 비교하여, 고유한 정수 지수를 결정한다.
지수는 를 만족하도록 계산된다. 이 비교를 통해, 원래 부동소수점 값()으로 다시 반올림되는 10진수 집합은 적어도 한 개의 원소를 포함하는 반면, 그보다 한 단계 더 세밀한 해상도()에서의 집합은 많아야 한 개의 원소만을 포함하게 됨이 보장된다.
이 접근 덕분에 알고리즘은 반복적이지(non-iterative) 않게 된다.
Schubfach는 Java의 BigInteger 같은 값비싼 임의 정밀도 연산을, 감소된 고정 정밀도 정수 연산으로 대체함으로써 높은 성능을 얻는다.
이런 효율적인 고정 정밀도 계산으로의 전환이 가능하고 또 올바른 것으로 보장되는 것은 Nadezhin 결과 덕분이다.
이 결과는, 반올림 구간의 중요한 스케일된 경계들이 정수에 극단적으로 가깝게 위치하지 않는다는 사실을 보인다. 구체적으로 말해, 이 경계들은, 정수에서 폭 인 영역 안에는(정수와 정확히 일치하는 경우를 제외하면) 존재할 수 없다.
이러한 분리(separation) 덕분에 알고리즘은, 미리 계산해 둔 10의 거듭제곱 테이블에서 얻은 제한된 정밀도의 과대 추정치(overestimate) 를 안전하게 사용할 수 있다. 이 근사치는 실제 값에 충분히 가까워서, 전체 정밀도 값(유리수나 big integer)을 사용했을 때와 동일한 반올림 결정을 내리게 해준다.
부동소수점 수는 단일 실수(real) 값만을 나타내지 않고, 그 값으로 다시 반올림되는 모든 실수를 포함하는 하나의 반올림 구간을 나타낸다. 유한한 양수 값 에 대해, 이 구간은 와 사이에 놓이며, 여기서 와 는 의 선행 값과 후행 값(바로 앞/뒤에 있는 표현 가능한 부동소수점 값) 사이의 중점이다. 일반적인 IEEE 754의 규칙적인 간격인 경우, 이들은 각각 와 이다. 2의 거듭제곱 근처의 드문 비규칙(interval spacing이 변하는) 경우에는 왼쪽 중점이 가 된다. 구간의 폭은 이고, 양 끝점을 제외한 사이의 모든 실수는 로 반올림된다. 어떤 끝점이 포함되는지는 반올림 모드에 따라 달라진다. 예를 들어, 짝수 반올림(round-to-even) 모드에서는, 가 짝수일 때는 양 끝점이 모두 에 속하고, 홀수일 때는 둘 다 제외된다.
부동소수점 값을 포맷할 때, 그 수의 완전한 10진 전개를 재현할 필요는 없다. 구간 안에 있는 어느 10진수라도 다시 로 반올림되는 것이 보장되므로, 목표는 그러한 수 중에서 자릿수(가수의 10진 자릿수 기준)가 가장 짧은 것을 선택하는 것이다. Schubfach는, 이 구간이 서로 다른 스케일()의 10진 격자(grid) 와 어떻게 교차하는지 살펴봄으로써 이를 수행한다. 격자 간격이 의 폭보다 좁으면, 그 스케일의 10진수 중 적어도 하나는 구간 안에 있어야 한다. 반대로, 간격이 더 넓으면, 많아야 하나만 포함될 수 있다. 이 전환이 정확히 어디에서 발생하는지를 찾음으로써, 알고리즘은 후보가 존재하는 최소 길이를 정확히 특정한다.
다음 그림은 이 원리를 시각적으로 보여 준다. 그림에는 선택된 10진 격자 상의 값들을 나타내는 고르게 간격을 둔 눈금이 있고, 반올림 구간은 수평 선분으로 그려져 있다. 격자 간격이 너무 거친 경우, 모든 눈금이 구간 밖에 놓일 수 있으므로, 그 길이의 10진수로는 를 표현할 수 없다. 간격이 너무 촘촘하면 여러 눈금이 구간 안에 들어가, 그 길이의 여러 10진수가 로 반올림된다. Schubfach는, 이 구간이 적어도 하나이면서 많아야 하나의 눈금을 포함하는 정확한 격자 레벨을 찾아냄으로써, 왕복 변환에서도 모호하지 않은 가장 짧은 10진수를 선택할 수 있게 해준다.
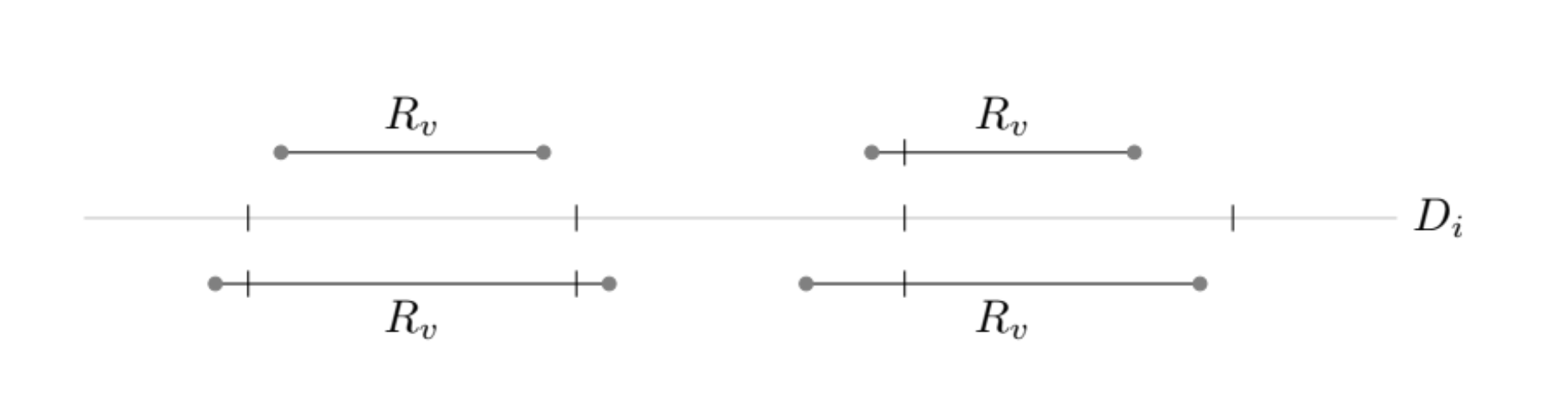
Raffaello Giulietti의 “The Schubfach way to render doubles”에서 가져온 그림으로, CC BY-SA 4.0 라이선스로 제공된다.
이제 https://github.com/vitaut/schubfach에 있는 구현을 살펴보자.
변환을 시작하기 위해 먼저 IEEE-754 구성 요소를 추출한다. 부호 비트, 지수 필드(bin_exp), 그리고 52비트 가수(bin_sig)이다. std::bit_cast를 사용하여 부동소수점 값을 부호 없는 정수로 해석한 뒤, 비트 연산으로 각 구성 요소를 추출한다:
uint64_t bits = std::bit_cast<uint64_t>(value);
constexpr int precision = 52;
constexpr int exp_mask = 0x7ff;
int bin_exp = static_cast<int>(bits >> precision) & exp_mask;
constexpr uint64_t implicit_bit = uint64_t(1) << precision;
uint64_t bin_sig = bits & (implicit_bit - 1); // binary significand부호는 바로 출력하고, ±무한대, NaN, 0 같은 특수한 경우는 바로 처리하여 문자열을 쓰고 일찍 반환한다:
if (bin_exp == exp_mask) {
memcpy(buffer, bin_sig == 0 ? "inf" : "nan", 4);
return;
}다음 단계는, 필요하다면 암시적 비트를 추가하고 지수를 조정하여 표현을 정규화하는 것이다:
bool regular = bin_sig != 0;
if (bin_exp != 0) {
bin_sig |= implicit_bit;
} else {
++bin_exp; // 서브노말에 대한 지수 보정.
regular = true;
}
bin_exp -= precision + 1023; // 지수 바이어스를 제거.이제 원래 수의 절댓값은 bin_sig * pow(2, bin_exp)와 같다.
또한, 반올림 구간이 규칙적(대칭)인지 여부를 결정한다. 불규칙성은 인접한 부동소수점 수들 사이의 간격이 증가할 때 발생하는데, 이는 서브노말이 아닌, 2의 거듭제곱 값들에서 일어난다.
반올림 구간의 경계를 정수로 만들기 위해 가수를 왼쪽으로 두 비트 시프트한다:
uint64_t bin_sig_shifted = bin_sig << 2;그리고 경계를 설정한다:
uint64_t lower = bin_sig_shifted - (regular ? 2 : 1);
uint64_t upper = bin_sig_shifted + 2;10진 지수(dec_exp, 논문에서는 )는 floor(log10(pow(2, bin_exp)))을 고정소수점 연산으로 계산해서 얻는다:
int dec_exp = regular ? floor_log10_pow2(bin_exp) : /* … */;여기서 floor_log10_pow2는 다음과 같이 정의된다:
// floor(log10(2) * 2**fixed_precision)
constexpr long long floor_log10_2_fixed = 661'971'961'083;
constexpr int fixed_precision = 41;
// e <= 5456721 에 대해 floor(log10(pow(2, e)))를 계산.
auto floor_log10_pow2(int e) noexcept -> int {
return e * floor_log10_2_fixed >> fixed_precision;
}불규칙한 구간(irregular interval)에 대해서는, 여기에 log10(3/4)에 대한 추가 보정이 더해진다.
이 10진 지수(정확히는 그 음수)는 이후 미리 계산해 둔 10의 거듭제곱 테이블에서, 126비트 가수 부분을 갖는 과대 추정치를 찾아내는 데 사용된다. 이 값들은 Python 스크립트 gen-pow10.py로 사전 계산된다. C++에는 표준 128비트 정수가 없기 때문에, 이 값들은 두 개의 uint64_t 값, 즉 pow10_hi와 pow10_lo로 반환된다.
흥미로운 점은, 테이블이 63비트 정수 쌍으로 값을 저장하고 있다는 것이다. 이는 아마도 이 알고리즘이 부호 없는 정수가 없는 Java를 겨냥했기 때문일 것이다. 현재 구현에서는 참조 코드와 최대한 가깝게 유지하기 위해 이 구조를 그대로 사용하지만, 앞으로는 단순화할 여지가 있다.
다음 단계는, 앞에서 얻은 10의 거듭제곱으로 가수와 경계를 곱하는 것이다:
uint64_t scaled_sig =
umul192_upper64_modified(pow10_hi, pow10_lo, bin_sig_shifted << shift);
lower = umul192_upper64_modified(pow10_hi, pow10_lo, lower << shift);
upper = umul192_upper64_modified(pow10_hi, pow10_lo, upper << shift);아마도 이 부분이 전체 알고리즘 중 가장 복잡한 부분일 것이다. 이 코드는, 이후 정수 후보들과 경계를 비교했을 때, 유리수나 bigint를 사용한 전체 정밀도 계산과 동일한 결과를 얻도록 해 주는 특수한(수정된) 반올림 방식에 의존한다. 또한 umul192_upper64_modified 내부의 중간 결과를 필요한 범위로 가져오기 위해, 작지만 다소 난해한 시프트가 적용된다. 자세한 내용은 이 글의 범위를 벗어나지만, 관심이 있다면 논문의 9.5, 9.6절을 참고하길 바란다.
이제 스케일링된 값과 경계를 얻었으므로, 최대 네 개의 후보를 만들고 그 중에서 선택할 수 있다.
dec_exp + 1()에 해당하는 두 후보 (이 중 구간에 들어갈 수 있는 것은 많아야 하나):
dec_sig_under2인 과소 추정(underestimate)dec_sig_over2인 과대 추정(overestimate)dec_exp()에 해당하는 두 후보 (적어도 하나는 구간에 속함):
dec_sig_under()인 과소 추정dec_sig_over()인 과대 추정검사는 매우 비슷하므로, 더 작은 10진 지수(dec_exp)의 경우만 살펴보자. 과소 추정이 구간 안에 있는지(under_in)를, 반올림을 위해 이진 가수의 최하위 비트(LSB)를 고려하면서 아래 경계와 비교하여 결정하고, 과대 추정에 대해서도 같은 방식으로 처리한다:
uint64_t dec_sig_under = scaled_sig >> 2;
uint64_t dec_sig_over = dec_sig_under + 1;
uint64_t bin_sig_lsb = bin_sig & 1;
bool under_in = lower + bin_sig_lsb <= dec_sig_under << 2;
bool over_in = (dec_sig_over << 2) + bin_sig_lsb <= upper;
if (under_in != over_in) {
// dec_sig_under와 dec_sig_over 중 정확히 하나만 반올림 구간에 있다.
return write(buffer, under_in ? dec_sig_under : dec_sig_over, dec_exp);
}둘 다 구간 안에 있다면, 더 가까운 쪽을 선택한다:
int cmp = scaled_sig - ((dec_sig_under + dec_sig_over) << 1);
bool under_closer = cmp < 0 || cmp == 0 && (dec_sig_under & 1) == 0;
return write(buffer, under_closer ? dec_sig_under : dec_sig_over, dec_exp);10진 가수를 선택한 뒤에는, 10진 지수(dec_exp)와 함께 write 함수에 넘겨 지수 표기(exponential format) 형태로 출력 버퍼에 기록한다. 우리는 모두 정수를 빠르게 포맷하는 법은 알고 있으니 이 부분은 자세히 다루지 않는다.
현재 구현은 Schubfach가 제안한 모든 최적화를 적용하지 않고, 단순성을 크게 해치지 않거나 correctness에 잠재적으로 해를 끼칠 수 있는 것들만 대체했다. 특히, 과 일 때 사용하는 논문 8.3절의 fast path는 생략했다. 이런 "최적화 예산 삭감"에도 불구하고, 이 구현을 여전히 Schubfach라고 부를 수 있기를 바란다.
이제 dtoa-benchmark(https://github.com/fmtlib/dtoa-benchmark)에서 이 기본 버전 알고리즘의 성능을 살펴보자:
| Function | Time (ns) | Speedup |
|---|---|---|
| ostringstream | 886.445 | 1.00x |
| sprintf | 736.517 | 1.20x |
| doubleconv | 83.057 | 10.67x |
| fpconv | 63.162 | 14.03x |
| grisu2 | 58.375 | 15.19x |
| ryu | 37.032 | 23.94x |
| schubfach | 34.801 | 25.47x |
| fmt | 22.391 | 39.59x |
| dragonbox | 20.706 | 42.81x |
| null | 0.932 | 950.76x |
| Function | Time (ns) |
|---|---|
| ostringstream | 886.445 |
| sprintf | 736.517 |
| doubleconv | 83.057 |
| fpconv | 63.162 |
| grisu2 | 58.375 |
| ryu | 37.032 |
| schubfach | 34.801 |
| fmt | 22.391 |
| dragonbox | 20.706 |
| null | 0.932 |
| Digit | ryu | doubleconv | fmt | dragonbox | fpconv | grisu2 | null | ostringstream | sprintf | schubfach |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 45.78 | 59.8 | 18.84 | 18.62 | 50.2 | 38.11 | 0.97 | 788.49 | 647.77 | 29.46 |
| 2 | 46.52 | 72.67 | 22.35 | 19.83 | 53.02 | 42.13 | 0.93 | 805.76 | 667.75 | 33.56 |
| 3 | 45.57 | 75.08 | 21.19 | 19.71 | 54.58 | 47.4 | 0.93 | 818.49 | 682.18 | 33.41 |
| 4 | 44.71 | 76.97 | 21.58 | 21.07 | 56.54 | 47.97 | 0.93 | 827.81 | 692.17 | 33.05 |
| 5 | 42.89 | 79.01 | 19.63 | 19.87 | 57.54 | 49.94 | 0.93 | 841.1 | 702.52 | 32.67 |
| 6 | 42.37 | 82.21 | 21.19 | 20.78 | 58.93 | 52.36 | 0.93 | 887.34 | 714.3 | 32.4 |
| 7 | 38.27 | 84.36 | 19.69 | 20.12 | 60.45 | 55.92 | 0.93 | 930.65 | 724.48 | 32.27 |
| 8 | 37.12 | 84.38 | 22.32 | 20.97 | 61.81 | 56.53 | 0.93 | 879.44 | 735.15 | 32.03 |
| 9 | 35.64 | 84.49 | 22.9 | 20.24 | 61.98 | 56.96 | 0.93 | 876.23 | 737.08 | 31.92 |
| 10 | 36.77 | 82.91 | 24.91 | 20.8 | 63.32 | 58.66 | 0.93 | 885.1 | 744.38 | 34.9 |
| 11 | 33.56 | 82.63 | 22.9 | 20.28 | 64.81 | 61.02 | 0.93 | 889.51 | 759.6 | 36.97 |
| 12 | 32.62 | 84.51 | 24.7 | 21.17 | 66.68 | 63.91 | 0.93 | 902.23 | 764.48 | 37.12 |
| 13 | 31.42 | 86.15 | 22 | 20.52 | 68.1 | 66.32 | 0.93 | 920.19 | 776.96 | 36.75 |
| 14 | 30.25 | 89.17 | 23.66 | 21.52 | 69.25 | 68.79 | 0.93 | 947.97 | 785.04 | 36.44 |
| 15 | 29.22 | 91.73 | 21.79 | 20.79 | 70.55 | 71.13 | 0.93 | 979.75 | 788.22 | 36.34 |
| 16 | 28.22 | 95.11 | 23.39 | 21.62 | 72.49 | 74.09 | 0.93 | 953.55 | 816.18 | 38.33 |
| 17 | 28.61 | 100.79 | 27.6 | 24.09 | 83.5 | 81.13 | 0.93 | 935.95 | 782.53 | 43.99 |
이 구현의 성능은 Ryu와 비슷하거나 약간 더 빠르며, Dragonbox보다는 약 70% 느리다. 반면 sprintf보다는 무려 21배나 빠르다. 생성된 테이블을 제외하면, 주석을 포함해 약 200줄의 코드만으로 이런 성능을 낸다는 점은 매우 인상적이다.
double 값을, 그 수의 최단 10진 표현으로 변환하는 최첨단 알고리즘을, 이식 가능한 C++ 코드 200줄 정도로 구현할 수 있다는 점은 대단히 인상적이다. 변경된(수정된) 반올림 단계를 제외하면, 일반적인 비트 다루기 기법에 익숙하다면 전체 구현은 비교적 직관적이다. 이 부분은 상당히 미묘한 논리라서, 필자도 완전히 내면화하기보다는 이식하는 데에 그쳤다. 때로는 수학을 믿을 수밖에 없는 순간이 있는 법이다.
이 구현의 성능은 기존 최고 수준 알고리즘과 경쟁할 만하며, __uint128_t 같은 몇 가지 확장을 적용하면 더 끌어올릴 수도 있다.
이 글이 도움이 되었기를 바란다. 전체 코드는 완화된 MIT 라이선스로 https://github.com/vitaut/schubfach에서 확인할 수 있다.
마지막 수정: 2025-11-29