Magic Kernel Sharp(매직 커널 샤프) 이미지 리사이징 알고리즘의 역사, 수학적 성질, 실용적 구현 방법과 참조 ANSI C 구현을 정리한 글.
URL: https://johncostella.com/magic/
Magic Kernel Sharp를 구현하고 싶다면 아래의 내 지침으로 바로 가면 되고, 도움이 필요하면 언제든 연락해 주세요.
이 논문(62쪽)은 Magic Kernel Sharp에 대한 완전한 수학적 분석을 제공하며, Lanczos 커널보다 우수한 이유를 보여줍니다.
난이도가 높지만 철저하고, 좋은 이미지와 그래프가 있습니다. Hacker News와 Facebook 페이지에서 일부 논의가 있었습니다.
오늘날 “매직 커널(the magic kernel)”은 구어적으로 Magic Kernel Sharp를 가리키는 말입니다. 이는 Facebook과 Instagram의 모든 사진을 처리하는 세계 표준급 이미지 리사이징 알고리즘이며, 이전의 사실상 표준이었던 Lanczos 커널을 거의 보편적으로 대체했습니다. 리사이즈된 이미지는 매우 선명하고, 확대가 아무리 크거나 축소가 아무리 작아도 다른 모든 알고리즘이 만들어내는 아티팩트가 놀라울 정도로 적습니다. 무엇보다도 Magic Kernel Sharp는 실제로 Lanczos 커널보다 계산 효율이 더 좋습니다.
나는 2006년에, 당시에는 “표준 JPEG 라이브러리”가 된 소스 코드에서 그때 내가 “매직”이라 부른 커널을 처음 접했습니다. 경험적으로 이 “커널”—실제로는 1/4과 3/4의 보간 가중치—을 사용하면 이미지를 두 배로, 원하는 만큼 여러 번 확대해도 놀라울 정도로 선명하다는 것을 발견했습니다. 하지만 전문가들은 결과 이미지가 이상적인 리사이저가 만들 결과보다 약간 더 흐리다고 지적했습니다.
2011년 나는 취미로 이 “매직” 커널의 놀라운 성질을 깊이 조사했고, 이미지를 임의의 크기(확대 또는 축소)로 리사이징할 수 있도록 일반화했습니다. 나는 이 일반화를 “Magic Kernel”이라고 불렀습니다.
2013년 초, Facebook에서 E6 소프트웨어 엔지니어로 일을 시작한 직후, 다른 엔지니어와 함께 Facebook에 업로드되는 모든 사진의 백엔드 리사이징 품질 문제를 다루는 사이드 프로젝트를 하던 중, Magic Kernel로 리사이즈한 _출력_에 간단한 3탭 샤프닝 단계(sharpening step)를 추가하면 거의 완벽에 가까운 충실도(fidelity)를 갖춘 빠르고 효율적인 리사이징 알고리즘이 된다는 것을 깨달았습니다. 나는 이 새 알고리즘을 Facebook 코드베이스에 구현하고 “Magic Kernel Sharp”라고 이름 붙였습니다.
이 알고리즘을 두 개의 독립된 부분—원래의 Magic Kernel 리사이징 단계 + 마지막 Sharp 단계—로 “인수분해(factorization)”한 것은 계산 효율을 더 좋게 만들었을 뿐 아니라, 같은 크기 필터링 함수와 비-안티앨리어싱 리사이징 함수만 제공하는 하드웨어 가속 라이브러리를 활용할 수 있게 해주었습니다. 그 결과, 2013년 중반까지 우리는 Facebook의 모든 이미지 백엔드 리사이징에 Magic Kernel Sharp를 배포할 수 있었고, 이는 대체한 코드 스택보다 품질이 더 좋을 뿐 아니라 CPU 및 저장소 효율도 더 좋았습니다. 이 코드는 이후 수조(trillions) 번 실행되었으므로 이러한 요소는 결정적이었습니다. (그 이후 Magic Kernel Sharp를 구현한 다른 사람들은 이런 극단적인 성능 제약이 없어서, 단일 커널로만 구현하기도 합니다.)
2015년 초, 나는 Magic Kernel Sharp 알고리즘의 푸리에(Fourier) 특성을 수치적으로 분석했고, 샘플링 주파수의 배수에서 고차 영점(high-order zeros)을 가진다는 것을 발견했습니다. 이것이 왜 결과가 그렇게 놀랍도록 선명한지 설명해 줍니다. 이 고차 영점들이, 그렇지 않으면 저주파 영역에 나타날 수 있는 잠재적 에일리어싱 아티팩트를 크게 억제하기 때문이며, 저주파 아티팩트는 시각적으로 특히 거슬립니다.
2015년 후반, 다른 소프트웨어 엔지니어가 Instagram을 Facebook의 백엔드 이미지 리사이징 인프라로 마이그레이션하려 했을 때, 기존 Instagram 스택이 Magic Kernel Sharp가 만드는 최종 이미지보다 더 “쨍함(pop)”이 있다는 사실을 알게 되었습니다. 나는 Sharp 단계에 이 추가 샤프닝을 포함하도록 Magic Kernel Sharp 코드를 조정하면 된다는 것을 깨달았습니다. 이를 통해 Instagram에 “Magic Kernel Sharp+”를 배포할 수 있었고, 역시 대체한 스택보다 CPU 및 저장소 효율이 더 좋고 품질과 해상도도 더 높았습니다.
2021년 나는 2013년 버전의 Magic Kernel Sharp를 약간 개선하여, 여전히 실용적이면서도 Sharp 단계의 이론적 스펙트럼 중립성(spectral neutrality)을 최소 9비트 정확도로 만족하는 커널을 얻었습니다. 나는 이 업데이트를 “Magic Kernel Sharp 2021”이라고 불렀고, 혼동을 피하기 위해 Facebook과 Instagram의 원래 버전은 “Magic Kernel Sharp 2013”이라고 부르기 시작했습니다.
대부분의 실용적인 이미지 리사이징 애플리케이션은 Magic Kernel Sharp 2013 또는 2021 또는 둘 다를 사용합니다. 이를 어떻게 하는지 아래에서 설명합니다. 어느 것을 선호해야 하는지에 “정답”은 없습니다. 시각적 품질과 계산 효율은 Facebook/Instagram이 사용하는 원래 2013 버전에서 최대이며, 다만 이미지가 약간 샤프닝됩니다(실제로 위에서 말했듯 Instagram은 이를 조금 더 샤프닝합니다). 2021 버전은 수학적으로 더 정확하고 스펙트럼이 평탄하여 눈에 띄게 샤프닝하지 않지만, 그 수학적 정확성 때문에 선명한 에지에서 더 많은 “깁스 링잉(Gibbs ringing)”이 생기며, 알고리즘도 원래 2013 버전보다 계산 효율이 낮습니다. 내 권장사항은, 스펙트럼 평탄성을 고집해야 할 강한 실용적/법적/이념적 이유가 없다면 2013 버전을 사용하라는 것입니다.
Magic Kernel Sharp 2021을 만든 뒤, 나는 다시 Magic Kernel Sharp의 수학적 성질을 파고들었습니다. (이 측면에 관심이 없으면 이 문단 나머지는 건너뛰어도 됩니다.) 나는 Magic Kernel의 푸리에 변환을 폐형식(closed form)으로 해석적으로 유도했고, 믿기지 않게도 _그것이 sinc 함수의 세제곱_임을 발견했습니다. 이는 Magic Kernel이 _직사각형 창 함수(rectangular window function)를 자기 자신과 두 번 컨볼루션한 것_과 같다는 뜻이며, 돌이켜보면 완전히 자명합니다. (수학적으로는 _cardinal B-spline_입니다.) 이 관찰과 Sharp 커널 요구조건의 정확한 정의를 결합하면, 정확한 Sharp 커널의 해석식을 얻을 수 있고, 따라서 정확한 Magic Kernel Sharp 커널도 얻을 수 있습니다. 그리고 이것이 리사이징의 근본 커널들의 _수열_에서 세 번째 항에 해당한다는 것을 알게 되었습니다. 이 발견은 Magic Kernel Sharp가 어떤 Lanczos 커널보다도 우수한 이유를 명시적으로 보여줄 수 있게 했습니다. 또한 이 근본 수열의 다른 항들도 유도할 수 있었는데, 특히 여섯 번째 항은 Lanczos-3와 같은 계산 효율을 가지면서 훨씬 더 우수한 성질을 가집니다. 이 결과는 위의 연구 논문에 자세히 설명되어 있습니다.
이 페이지의 나머지에서는 Magic Kernel Sharp의 발전 역사에 대한 간단한 개요를 제공하고, 직접 구현하는 방법을 설명합니다.
Magic Kernel Sharp의 무료 오픈소스 참조 ANSI C 구현은 이 페이지 맨 아래에 있습니다. MIT-0 라이선스로 제공됩니다. Magic Kernel Sharp를 직접 구현하려는 경우가 아니라면 이 참조 구현을 빌드/실행할 필요는 거의 없을 것입니다. 이미 ImageMagick 같은 표준 유틸리티에 내장되어 있기 때문입니다(다소 아이러니하게도, 2013년 Facebook에서 Magic Kernel Sharp를 당시의 표준이던 Lanczos-3 커널과 비교 테스트하는 데 ImageMagick을 사용했습니다).
Magic Kernel Sharp를 구현하는 누구든 돕게 되어 기쁩니다. 언제든 직접 연락해 주세요.
내가 어떻게 이미지 처리에 발을 들였는지에 대한 중요하지 않은 전사는 젊은 소프트웨어 엔지니어들에게 흥미로울 수 있으며, 여기에 있습니다.
2006년, 나는 당시에는 “the IJG JPEG library”(오늘날 표준 JPEG 라이브러리)라고 불리던 코드들을 보고 있었습니다. 표준 JPEG 압축은 두 개의 색차(chrominance) 채널 데이터를 반 해상도에 저장합니다. 즉, 2 x 2 픽셀 블록마다 Cr 하나와 Cb 하나만 저장합니다. 따라서 이미지를 복원할 때 색차 채널을 다시 전체 해상도로 “업샘플링(upsample)”해야 합니다.
가장 단순한 업샘플링은 각 2 x 2 블록을 나타내는 값 하나를 그 블록의 네 픽셀 모두에 복제하는 것인데, 이를 “최근접 이웃(nearest neighbor)” 업샘플링이라 부릅니다(이 경우 “이웃”은 사실상 그 2 x 2 블록에 대해 저장된 단일 값입니다). IJG 라이브러리는 기본으로 이 방법을 사용했지만, “fancy upsampling”이라는 선택 모드도 제공했습니다. 아래 예시는 복원 결과의 차이를 보여줍니다(특히 빨강과 검정 사이의 경계에 주목하세요).

색차 채널의 최근접 이웃 업샘플링

색차 채널의 “fancy” 업샘플링
흥미가 생겨 나는 이 “fancy” 업샘플링의 C 소스 코드를 살펴보았습니다. 놀랍게도, 그것은 각 방향으로 단순 보간(interpolation)일 뿐이었고, 가까운 2 x 2 블록 중심에는 3/4 가중치, 먼 2 x 2 블록 중심에는 1/4 가중치를 주는 방식이었습니다! 다른 관점으로는 각 방향에 대해 {1/4, 3/4, 3/4, 1/4} 값을 갖는 “커널”이라고 볼 수 있습니다(이 표기에서 표준 “복제”/“최근접” 커널은 {0, 1, 1, 0}입니다).
더 흥미가 생긴 나는 이 커널을 JPEG가 아닌 일반 이미지의 세 채널 모두(색차 채널뿐 아니라)에 적용해 보았고, 그 결과 각 방향으로 이미지가 2배 확대되도록 했습니다. 놀랍게도 이 커널은 “매직”처럼 보였습니다. 몇 번을 반복 적용하든, 반복 확대에서 놀라울 정도로 좋은 결과를 주었습니다.

원본 이미지

“매직” 커널로 한 번 2배 확대

두 번 2배 확대

세 번 2배 확대
마찬가지로 다운샘플링 커널로 적용하면, 매우 아름답게 안티앨리어싱된 이미지를 얻을 수 있었습니다.

새 원본 이미지

“매직” 커널로 한 번 1/2 축소

두 번 1/2 축소

세 번 1/2 축소
위의 서론에서 설명했듯, 이 이미지들은 모두 필요 이상으로 더 흐립니다. 이는 Magic Kernel Sharp의 후처리 샤프닝 단계를 추가하는 일이 당시로서는 아직 7년 뒤였기 때문입니다.
신호 처리 이론과 에일리어싱 아티팩트에 익숙했던 나는, 이 “매직” 커널이 어떻게 이런 놀라운 결과를 내는지 이해할 수 없었습니다.
충격을 받은 나는, 교과서나 웹 어디에서도 이 커널을 찾지 못해, 뉴스그룹에 이것이 잘 알려진 것인지 물어보았습니다. 이 절의 제목과 같은 제목(“ ‘Magic’ kernel for image zoom resampling?”)으로요: 여기와 여기를 보세요. 잘 알려진 것은 아닌 듯했습니다.
이론적으로 완벽한 안티앨리어싱 커널은 _sinc 함수_입니다. 실용적으로는 무한 지지(support) 때문에 Lanczos 커널 같은 근사가 필요합니다.
그렇다면 очевид한 질문은 이것이었습니다. 어떻게 단순한 {1/4, 3/4, 3/4, 1/4} 커널이 이미지를 확대할 때 그렇게 잘할 수 있는가?
2006년, 내가 올린 글 이후의 뉴스그룹 토론에서 “매직” 커널이 사실상 매우 단순한 sinc 근사라는 점이 밝혀졌습니다. 다만 새로운 샘플링 위치가 원래 위치에서 반 픽셀만큼 오프셋되어 있다는 비틀림이 있습니다. (원래 JPEG 색차 구현의 “타일링”을 생각하면 자명하지만, 샘플링 이론 관점에서는 전혀 자명한 선택이 아닙니다.)
하지만 이것만으로는 왜 그렇게 잘 작동하는지 설명되지 않았습니다. sinc의 다른 많은 근사는 안티앨리어싱을 전혀 잘하지 못합니다.
어쨌든 나는 이런 이론적 질문은 제쳐두고, 이 “매직” 커널을 밉매핑(점진 다운로드) 방법에 실용적으로 사용했으며 이를 JPEG-Clear라고 불렀습니다.
JPEG-Clear를 개발한 뒤 이미지 처리 작업은 뒷전이 되었습니다. 2007년에 더 도전적인 본업—사설 헤지펀드의 알고리즘 개발/구현—으로 옮겼기 때문입니다.
“매직” 커널의 이론적 미스터리는 이후 5년 동안 계속되었습니다.
그러나 2011년에는 다시 일이 바뀌어, 전립선암 연구를 위한 영상 및 체적(volumetric) 데이터를 처리하는 일을 하고 있었습니다. 그 작업의 일부로 (전립선 경계를 찾기 위한) 에지 검출 알고리즘을 보고 있었습니다.
나는 “매직” 커널을 사용하여, 표준 방법의 일부 함정을 피하는 에지 검출 연산자를 만들 수 있다는 것을 깨달았습니다.
내 에지 검출 논문은 Charles Bloom의 관심을 끌었고, 그는 특히 “매직” 커널을 상당히 자세히 분석했습니다. 에지 검출기 자체에 대한 논의는 다른 곳에 맡기더라도, Bloom은 “매직” 커널이, “두 배(또는 타일링)” 격자에 대한 최근접 업샘플링(즉 {1, 1}) 이후, 그 새 공간에서의 {1/4, 1/2, 1/4} 정규 커널로의 컨볼루션으로 인수분해될 수 있음을 지적했습니다.
이것도 여전히 왜 업/다운사이징을 그렇게 잘하는지 설명하진 못했지만, 그 성질을 더 탐구하고 싶은 내 관심을 다시 불러일으켰습니다.
Bloom의 인수분해 이후 나는 다시 이것저것 실험했습니다. 그리고 이 커널을 자기 자신과 임의 횟수만큼 컨볼루션해도 결과 커널은 항상 구간별 포물선(piecewise parabolic)—세 개의 포물선이 매끄럽게 이어지는 형태—임을 경험적으로 발견했습니다. 이로 인해 커널은 상수 소스 신호와 컨볼루션될 때 “자기 안에 맞춰 들어갑니다”(수학적으로: partition of unity; 아래에서 다시 다룹니다).
이를 논리적으로 끝까지 밀고 가, 신호가 “매직” 커널로 무한히 업샘플링된다면 어떤 일이 생기는지 보았습니다. 원래 샘플 공간에서의 좌표를 x(원 신호는 x의 정수값에서 샘플됨)라 하면, 값들의 수열을 직접 관찰하는 것만으로, 무한 업샘플링된 Magic Kernel 함수는 다음 해석식으로 주어짐을 유도했습니다.
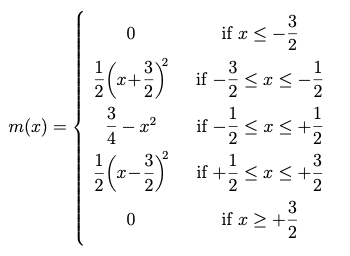
Magic Kernel의 해석식
m(x)의 그래프는 다음과 같습니다.
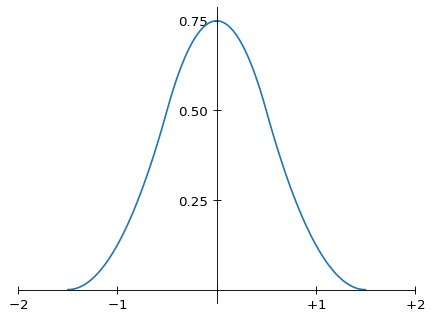
Magic Kernel의 그래프
이것은 sinc 함수처럼 보이지 않습니다. 그렇다면 어떻게, 왜 이미지 확대에 그렇게 잘 작동할까요?
첫째, m(x)는 유한 지지를 가집니다. 원 신호의 한 샘플은 그 위치에서 왼쪽 1.5 간격부터 오른쪽 1.5 간격까지의 영역에만 기여합니다. 따라서 구현이 실용적입니다.
둘째, m(x)가 음이 아닌(nonnegative) 것이 편리합니다. 이는 “링잉(ringing)”을 유발하지 않고, 출력 이미지의 동적 범위가 입력과 정확히 같도록 보장합니다.
셋째, m(x)는 연속이며 1차 미분도 어디서나(지지의 끝에서도) 연속입니다. 커널 또는 그 1차 미분의 불연속은(끝점이라 하더라도) 일반적으로(대개 미묘하지만) 사람이 알아차릴 수 있는 아티팩트를 유발하므로, 이 성질은 컨볼루션 결과가 “좋아 보이게” 합니다.
넷째, _m(x)는 unity의 분할(partition of unity)_입니다. 정수 위치마다 m(x)를 복사해 놓고 합하면 모든 x에서 상수(1)가 됩니다. 양 끝의 볼록 포물선이 가운데의 오목 포물선과 정확히 맞아떨어집니다.
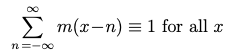
partition of unity 항등식
이 놀라운 성질은 리사이즈 이미지 전반에 걸친 “비트(beat)” 아티팩트를 방지하는 데 도움을 줄 수 있습니다.
다섯째, m(x)의 형태는 시각적으로 가우시안(Gaussian)과 닮아 있는데, (푸리에 이론을 모른다면) 수학자가 보간 커널로 자연스럽게 선택할 법한 모양입니다. 위의 함수 형태로부터 m(x)의 표준편차는 1/2임을 계산할 수 있습니다. 같은 표준편차를 갖는 가우시안과 비교하면, 닮은 것이 착시만은 아님을 알 수 있습니다.
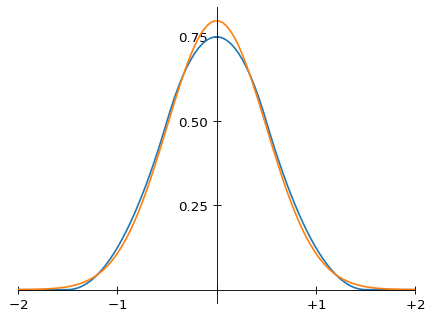
Magic Kernel과 가우시안 비교
흥미롭게도, 1980년대 초 피라미드 인코딩의 기념비적 연구에서도 계수 {0.05, 0.25, 0.4, 0.25, 0.05}의 5탭 필터에서 정확히 같은 가우시안 유사 성질을 찾았습니다(여기와 여기).
반면 sinc 함수는 진동하는 로브(lobe)를 가져, 매끄러운 보간 함수로 직관적인 선택이 아니며, 실제로는 강제로 절단(truncation)해야 합니다.
가우시안과 달리 m(x)는 유한 지지이므로, 자기 안에 맞춰 들어가기 위해 인접한 세 개의 복사본만 필요합니다. 따라서 가우시안을 실용적으로 쓰기 위해 유한 지지로 절단하면 왜 아티팩트가 생기는지도 이해할 수 있습니다. 절단된 가우시안은 “자기 안에 맞춰 들어가지” 못하기 때문입니다(즉 partition of unity가 아닙니다).
서론에서 언급했듯, 2013년 초 Facebook의 E6 소프트웨어 엔지니어로서 부트캠프를 막 마쳤을 때, 경험 많은 엔지니어 Vjeux로부터 Kevin Dale이 Facebook의 모든 사진을 고치려 한다는 이야기를 들었습니다. 문제는 JPEG 압축 때문이라고 믿어지고 있었습니다. 부트캠프에서는 소프트웨어 엔지니어가 “가장 큰 임팩트가 있다”고 판단되는 어떤 것이든(매니저를 설득할 수만 있다면) 할 수 있다고 들었습니다. (역사를 바꾸게 해준 Itamar에게 감사!) 나는 내 JPEG UnBlock 알고리즘을 만든 경험으로 정확한 원인을 찾아낼 수 있다고 생각했습니다.
결론부터 말하면, JPEG가 문제가 아니었습니다. 나는 품질 문제의 근본 원인이, 서버에서 모든 이미지를 리사이즈하는 데 쓰이던 하드웨어 가속 라이브러리의 근본적 한계임을 빠르게 밝혀냈습니다. JPEG 압축은 전혀 문제가 아니었습니다.
그 발견만으로도 신입 엔지니어로서는 괜찮은 기여였을 겁니다. 하지만 벽의 포스터들이 계속 나를 부추겼습니다. “Facebook에서는 아무것도 남의 문제가 아니다.” 그래서 내가 고쳐야 할 문제라고 결심했습니다.
하지만 어떻게? 그 하드웨어 라이브러리는 안티앨리어싱 리사이저를 아예 제공하지 않았습니다. 그리고 하루에 수십억 장의 이미지를 리사이즈해야 했으니, 그 하드웨어 라이브러리에 의존하지 않는 것은 불가능했습니다.
매뉴얼을 몇 시간이나 멍하니 바라보다가, 완전히 바보 같은 아이디어가 떠올랐습니다. 하드웨어 라이브러리에서 정상적으로 작동하는 조각들—같은 크기 필터링과 비-안티앨리어싱 리사이징—을 해킹으로 조합해, 안티앨리어싱 리사이저처럼 동작하게 만들 수 있지 않을까?
이 해킹은 필터가 어디서나 음이 아닌 경우에만 작동한다는 것을 즉시 알았습니다.
그리고 나에게는 그런 필터가 있었습니다. 바로 Magic Kernel!
나는 코드를 썼고, 작동했습니다! 나는 황홀했습니다.
하지만 곧 폭탄이 떨어졌습니다. Kevin은 수백만 장의 테스트 이미지 코퍼스를 가지고 있었고, 일반적인 이미지 오류 척도로, 프로덕션 코드와 “골드 스탠다드”(비효율적이지만)인 세계 최고 커널 Lanczos-3 구현과 비교해 어떤 변경도 테스트하고 있었습니다. 그리고 그는 전문가들이 2006년 6월부터 2013년 1월까지 6년 넘게 내게 말해오던 것을 빠르게 증명했습니다. Magic Kernel은 이미지를 흐리게 만든다. 심하게. 오류는 끔찍했습니다.
거의 끝이었습니다.
하지만 나는 생각했습니다. 결과가 흐리면, 그냥 다시 샤프닝하면 안 되나?
나는 다음 사고 실험을 했습니다. Magic Kernel을 이미지에 적용하되 리사이징은 전혀 하지 않는다면? 즉 같은 크기 필터로 적용하여, 출력 샘플링 격자가 입력 격자와 동일하다면?
위 그래프에서 분명히 보이듯, 이는 이미지가 약간 흐려짐을 의미합니다. 공식에서 필터 가중치는 −1, 0, +1 위치에서 {1/8, 3/4, 1/8}이 됩니다.
이것이 바로 Magic Kernel이 리사이즈 이미지들을 흐리게 만드는 이유이며, 2006년 6월부터 2013년 1월까지 전문가들이 내게 계속 말하던 것입니다.
그 다음, 내가 생각할 수 있는 가장 단순한 샤프닝 필터를 적용하기로 했습니다. 3탭이고 샤프닝 양을 정하는 자유 매개변수 하나가 있는 형태입니다. 몇 줄의 대수 계산으로, 전체 커널이 −1과 +1 위치에서 0이 되게 하는 매개변수 값을 찾았습니다. 결과는 빠르게 나왔습니다. {−1/4, +3/2, −1/4}.
따라서 새 해결책은: Magic Kernel 코드 해킹으로 이미지를 리사이즈한 뒤, 결과에 이 샤프닝을 적용하는 것입니다(당시에는 다운사이징만 보고 있었으므로 작동). 리사이징이 전혀 없을 때 전체 커널은 {−1/32, 0, +17/16, 0, −1/32}가 됩니다. 델타 함수는 아니지만 매우 가깝습니다. ±1 위치에 의도된 영점이 있고, ±2 위치에 −3% 로브, 0 위치에 +6% 초과가 있습니다. Magic Kernel이 유발하던 약간의 블러 대신, 이제는 약간의 잔여 _샤프닝_이 남습니다.
나는 이 해킹을 “Magic Kernel Sharp”라고 불렀습니다.
그리고 이것이 Facebook 사진들을 구동합니다.
2015년 초까지 Facebook 서버는 2년 동안 Magic Kernel Sharp를 훌륭한 결과로 사용하고 있었습니다. 나는 Photos를 그 초기의 한 번짜리 사이드 프로젝트 이후로 작업하진 않았지만, 신호 이론 관점에서 Magic Kernel Sharp 커널이 왜 그렇게 놀랍도록 잘 작동하는지 더 이해하고 싶었습니다. 이는 Magic Kernel m(x)
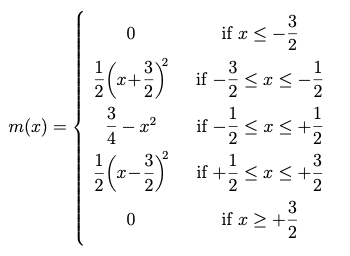
Magic Kernel의 해석식

Magic Kernel의 그래프
과, 2013년에 유도한 Sharp 커널, 즉 [−m(x−1) + 6m(x) − m(x+1)] /4 의 컨볼루션일 뿐이라는 것을 떠올리세요. 이 컨볼루션을 수행하여 Magic Kernel Sharp(2013) 커널의 해석식을 얻었습니다.
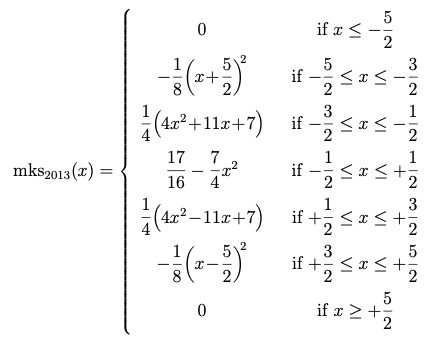
Magic Kernel Sharp(2013)의 해석식
그래프로는 이제 다섯 개의 포물선으로 이루어집니다.
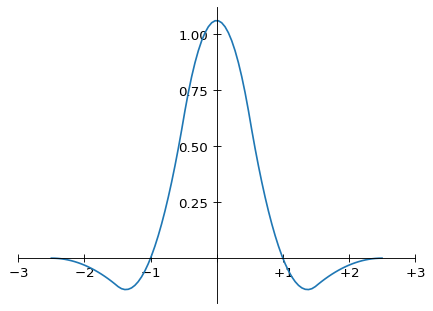
Magic Kernel Sharp(2013)의 그래프
이를 Lanczos-2 커널과 비교해 봅시다.
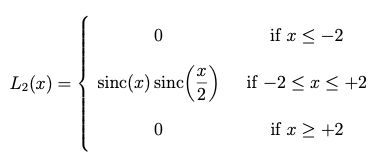
Lanczos-2 커널의 해석식
그래프는 다음과 같습니다.
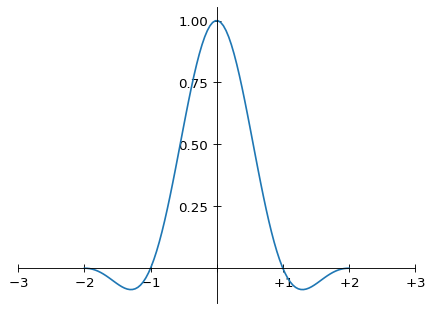
Lanczos-2 커널의 그래프
또한 푸리에-이상적인 sinc 함수는 같은 구간에서 다음과 같습니다.
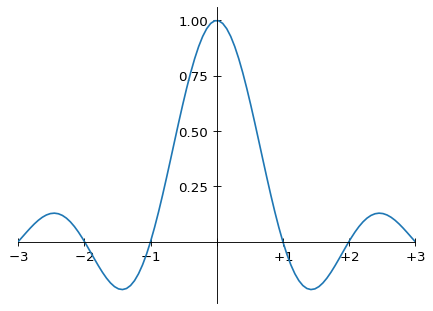
이상적 sinc 함수 커널의 그래프(−3에서 +3)
(물론 무한 지지를 가지므로 이 구간 밖으로 계속됩니다.) 위에서 말했듯 Magic Kernel Sharp 2013 커널(이제부터 “2013” 괄호는 생략)은 여기 보인 다른 두 커널처럼 x=±1의 샘플링 위치에 영점이 있지만, x=±2에는 영점이 없습니다. 반면 Lanczos-2보다 음의 로브에 더 많은 가중치가 있습니다. 전체적으로는 Magic Kernel Sharp 2013과 Lanczos-2의 모양이 꽤 비슷해 보입니다.
하지만 Magic Kernel Sharp 2013 커널의 안티앨리어싱 성질을 충분히 이해하려면 푸리에 공간으로 가야 했습니다. 나는 푸리에 변환을 수치적으로 수행하기로 했습니다. 참고 및 코드 검증을 위해, 임의로 선택한 유한 개의 푸리에 계수를 사용해 이상적 sinc 필터의 수치 푸리에 변환을 수행했습니다.
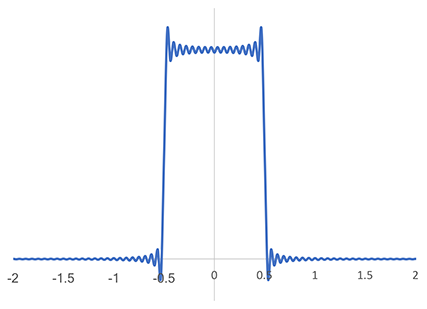
sinc 커널의 푸리에 변환 수치 근사
여기서, 유한 계수 선택으로 인한 깁스 현상(링잉)을 볼 수 있습니다. 이상적 sinc 필터는 나이퀴스트 영역(브릴루앙 존) 안에서 1이고 밖에서 0입니다(이 그래프 단위에서 나이퀴스트 주파수는 1/2).
같은 방식으로 Lanczos-2 커널을 분석하면 다음을 얻습니다.
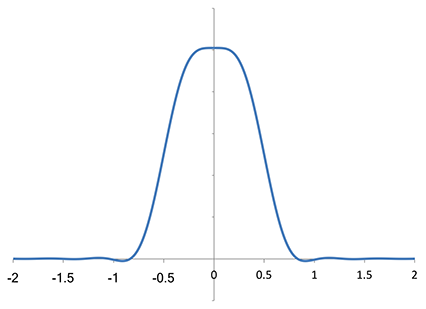
Lanczos-2 커널의 푸리에 변환(동일한 수치 근사)
나이퀴스트 영역 안의 고주파 성분을 감쇠하기 시작하고, 영역 밖의 주파수를 계속 억제하며, 축을 교차할 때까지 감소합니다. 주목할 점은 나이퀴스트 주파수의 두 배, 즉 샘플링 주파수(f=±1)에서 영점을 갖는다는 것입니다. 이 영점이 중요한 이유는, 샘플링은 원 스펙트럼의 복사본을 모든 정수 위치에 놓으므로 샘플링 주파수(및 그 배수)는 샘플링에 의해 0 주파수로 폴드오버(foldover)되기 때문입니다. f=±1에서 0이면 인접 복사본에서 0 주파수로 내려오는 것이 없다는 뜻입니다.
이제 Magic Kernel Sharp 2013 커널의 푸리에 변환을 수치적으로 분석하면 다음을 얻습니다.
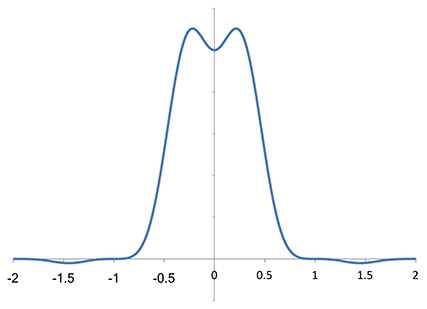
Magic Kernel Sharp 2013의 푸리에 변환(동일한 수치 근사)
약간 상승했다가 0으로 떨어지기 시작하지만, 첫 번째 나이퀴스트 존 안에서는 Lanczos-2 스펙트럼과 꽤 비슷합니다. 하지만 내 눈에는 _Magic Kernel Sharp 2013이 f=±1(및 f=±2)에서 더 높은 차수의 영점_을 갖는 것처럼 보였습니다. 세로축을 확대해 보았습니다.
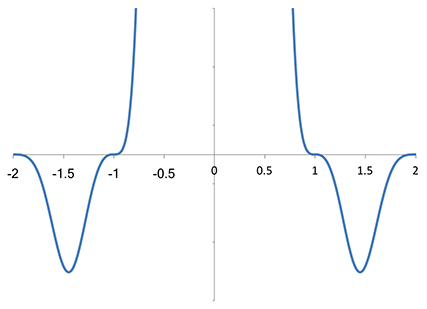
Magic Kernel Sharp 2013 푸리에 변환의 세로 확대
Magic Kernel Sharp 2013 커널이 샘플링 주파수의 정수 배에서 실제로 고차 영점(즉 변곡의 정상점)을 가짐이 분명합니다. 이것이 뛰어난 시각적 안티앨리어싱 성능을 설명합니다: 저주파 아티팩트는 특히 거슬리는데, 이 고차 영점은 샘플링 에일리어싱 이후 저주파 공간의 상당 부분이 그러한 아티팩트로부터 대체로 깨끗하도록 보장해 줍니다. 단지 0 주파수 주변의 아주 작은 영역만이 아닙니다.
Lanczos-2 커널의 스펙트럼을 같은 스케일로 확대하면
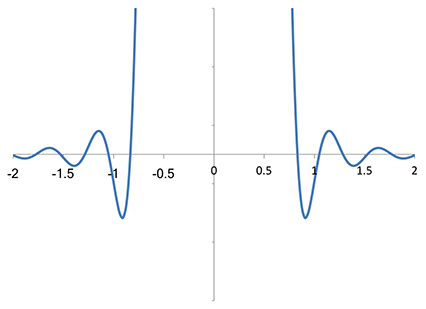
Lanczos-2 커널 푸리에 변환의 동일한 세로 확대
상당히 놀라운 사실을 관찰했습니다. Lanczos-2 커널은 사실 샘플링 주파수의 정수 배에서 영점을 갖지 않습니다. 두 번째 영점이 샘플링 주파수보다 약간 높은 주파수에 있을 뿐 아니라(여기 스케일에서 f=−1 바로 아래, f=+1 바로 위), 더 중요한 것은 그것이 1차 영점뿐이라는 점입니다(즉 축을 거의 선형으로 “가로지르며” 통과). Magic Kernel Sharp 2013에서 보이는 것처럼 정상점은커녕 변곡 정상점도 아닙니다. Lanczos-2의 이 근사 영점이 전반적으로 저주파 영역으로의 폴드오버를 꽤 억제하긴 하지만, 샘플링 주파수 정확히 위치한 Magic Kernel Sharp 2013의 고차 영점(그리고 그 배수들에서의 고차 영점)과는 비교할 수 없습니다.
서론에서 언급했듯, Instagram 엔지니어 Georges Berenger가 Instagram에도 Facebook의 리사이징 코드를 쓰고 싶다며 내게 왔을 때, 그는 Instagram 이미지가 Magic Kernel Sharp 2013이 Facebook용으로 만드는 이미지보다 더 샤프하다는 것을 빠르게 증명했습니다. 그는 물었습니다. 고칠 수 있나? 고칠 수 없다면 Instagram에 배포할 수 없다고요.
나는 배포된 2013 코드를 다시 보고, Sharp 단계를 {−s, 4+2s, −s} /4 형태로 해킹하면, s 값을 바꾸어 원하는 만큼의 추가 샤프닝을 제공할 수 있고—공짜라는 것을 깨달았습니다. s=0은 항등 커널(샤프닝 없음), s=1은 Magic Kernel Sharp 2013에 필요한 샤프닝, s=2는 두 배 샤프닝… 이런 식입니다.
우리는 s=1.32가 Instagram에 필요한 정도를 만든다는 것을 찾았습니다.
이 “Magic Kernel Sharp+”는 다른 사람들이 반드시 써야 하는 별도 버전을 의도한 것은 아닙니다. 추가 계산 비용 없이 리사이즈된 이미지가 더 “쨍하게(pop)” 보이도록 하는 단순한 해킹일 뿐입니다.
하지만 Instagram의 모든 사진을 구동하는 해킹이기도 합니다.
그리고 이 샤프니스 문제는 6년 뒤 Magic Kernel Sharp의 다음 진화로 이어졌습니다.
위에서 Magic Kernel Sharp 2013 커널의 독특한 푸리에 성질이, 특히 저주파에서 에일리어싱 아티팩트가 매우 적은 이유를 설명해 준다는 것을 보았습니다. 대부분의 실용적 다운사이징에서는 위에서 설명한 대로 그대로 적용하면 충분합니다(실제로 대규모로 그렇게 해왔습니다).
하지만 위에서, k→1 극한에서 커널이 {−1, 0, +34, 0, −1} /32로 접근하며, 이는 입력 이미지의 약간의 샤프닝이라는 점을 언급했습니다. 실제로 이렇게 변환된 일부 이미지에서 이 샤프닝을 알아차릴 수 있습니다. (2차 도함수가 꽤 일정한 영역에서는, Sharp 단계가 제공해야 할 샤프닝의 50%를 추가로 기여합니다.) 자연스러운 질문은: 잔여 샤프닝을 가능한 제거하여 k→1 극한에서 항등에 더 가까운 것을 만들 수 있도록 한 단계 더 개선할 수 있을까?
가능합니다. 커널 {1, 0, 34, 0, 1} /36을 추가로 컨볼루션해 보세요. 이것 자체는 약간의 블러입니다. 결과는 {−1, 0, 0, 0, 1154, 0, 0, 0, −1} /1152가 됩니다. 이는 항등에 매우 가깝고, 이미지에서 일반적으로 쓰는 8비트 동적 범위 아래에서는 그 자체로 항등입니다.
따라서 2021년 나는 다음 가정을 세웠습니다. 2021 버전 Magic Kernel Sharp 커널에는 이 추가 컨볼루션이 포함되어야 한다.
이 개선을 어떻게 볼까요? 이는 아마도 _Sharp 2013 커널 자체의 개선_이라고 할 수 있습니다. 2013년에 나는 3탭 샤프닝 커널 {−1, +6, −1} /4를 단순히 가정했지, 이것이 이상적인 형태인지 따지지 않았습니다. (사실 샤프닝 양은 약간 달랐는데, 수백만 장 테스트 코퍼스에 대해 Lanczos-3 대비 오류 손실이 최소가 되도록 조정했기 때문이지만, 대략 이와 가까웠습니다.) 위의 고려는, 이를 {1, 0, 34, 0, 1} /36과의 컨볼루션으로 수정해야 함을 시사합니다. 즉 {−1, +6, −35, +204, −35, +6, −1} /144입니다. 이 “Sharp 2021” 커널을 Magic Kernel 이후에 적용하는 Sharp 단계의 최선의 실용적 정의로 삼겠습니다.
따라서 실용적으로 Magic Kernel Sharp는 더 단순한 3탭 Sharp 2013 커널 {−1, +6, −1} /4를 사용하여 Magic Kernel Sharp 2013을 만들거나, 더 높은 충실도의 Sharp 2021 커널 {−1, +6, −35, +204, −35, +6, −1} /144를 사용하여 _Magic Kernel Sharp 2021_을 만들 수 있습니다. 후자는 최소 9비트 정확도로 이미지를 블러나 샤프닝하지 않습니다.
그래프로 보면 Magic Kernel Sharp 2021은 다음 커널입니다.
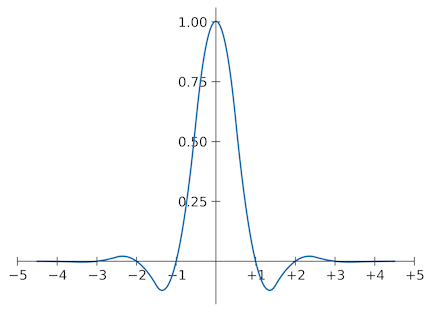
Magic Kernel Sharp 2021의 그래프
서론에서 언급했듯, 2021년에 나는 Magic Kernel의 푸리에 변환을 폐형식으로 해석적으로 유도했고, 그것이 _sinc 함수의 세제곱_임을 발견했습니다. 이는 Magic Kernel이 _직사각형 창 함수를 두 번 자기 자신과 컨볼루션한 것_이라는 뜻입니다(수학적으로는 cardinal B-spline). 이 관찰과 Sharp 커널 요구조건의 정확한 정의로부터, 정확한 Sharp 커널과 따라서 정확한 Magic Kernel Sharp 커널의 해석식을 얻었습니다. 그리고 이것이 리사이징의 근본 커널 수열에서 세 번째 항임을 인식했습니다. 이 결과는 Magic Kernel Sharp가 어떤 Lanczos 커널보다도 우수한 이유를 명시적으로 보여줄 수 있게 했고, 더 나아가 이 수열의 다른 항들, 특히 Lanczos-3와 동일한 계산 효율을 가지면서 성질은 훨씬 우수한 여섯 번째 항도 유도할 수 있게 했습니다. 이 결과는 다음 논문에 자세히 설명되어 있습니다.
위 논문에서는 위의 푸리에 스펙트럼 관찰을 바탕으로 Magic Kernel Sharp가 Lanczos 커널보다 나은 이유를 매우 자세히 분석합니다. 하지만 가장 쉬운 방법은, 두 가지 대표 예제를 직접 보는 것입니다.
첫째는 가우시안 블롭을 확대한 경우입니다.

Lanczos 커널의 픽셀화 문제를 Magic Kernel Sharp가 갖지 않음을 보여주는 논문 그림 35
확대에서 Lanczos 커널의 결함은 이런 픽셀화 문제로 이어질 수 있습니다.
둘째는 수직 격자(vertical grating)를 축소한 경우입니다.

Lanczos 커널의 비트 문제를 Magic Kernel Sharp가 갖지 않음을 보여주는 논문 그림 37
축소에서 같은 결함이 이런 비트 문제로 이어질 수 있습니다.
이 문제 회피는 전적으로 Magic Kernel Sharp의 Magic Kernel 부분에서 옵니다. 2013 버전을 쓰든 2021 버전을 쓰든 상관없습니다. 둘 다 Lanczos 커널에 내재한 근본 결함과 아티팩트를 가지지 않습니다.
2021년 2월 이 페이지를 Magic Kernel Sharp 2021로 업데이트한 뒤, 리사이징 라이브러리/애플리케이션 작성자들이 내게 반복적으로 물었습니다. 실제로는 어떻게 구현하나요? 2022년 11월, 나는 그 답을 논문과 아래 ANSI C 구현에 묻어두었던 것을 사과하며, 다음 내용을 추가했습니다.
일반적으로 Magic Kernel Sharp 2021은 실무에서 세 가지 방식으로 구현할 수 있습니다.
이 때문에 (3)의 “직접” 구현을 위한 전체 Magic Kernel Sharp 2021 커널의 명시적 공식을 여기 제공합니다.

Magic Kernel Sharp 2021의 해석식
동등하면서 약간 더 계산 효율적일 수 있는 대체 식은 다음입니다.

Magic Kernel Sharp 2021의 대체 식
마찬가지로 Magic Kernel Sharp 2013에 대한 동등한 대체 식도 있습니다.

Magic Kernel Sharp 2013의 대체 식
(lakshayg가 ImageMagick에 Magic Kernel Sharp를 구현하면서 수행한 단순화에 감사드립니다.)
Magic Kernel Sharp를 구현하는 누구든 돕게 되어 기쁩니다. 언제든 직접 연락해 주세요.
이제 위 공식들을 여러분의 이미지 리사이징 라이브러리/앱에 넣었다고 합시다. 구현이 정확한지 쉽게 테스트하려면 어떻게 해야 할까요?
2024년 12월 나는 참조 C 구현에 두 프로그램을 추가해, 이 테스트를 비교적 쉽게 만들었습니다.
먼저 그 중 하나로 “커널 테스트 입력(kernel test input)” 이미지를 만듭니다. Magic Kernel Sharp 2013의 경우:
$ make_kernel_test_input 5 mks-2013-input.png
첫 번째 인자 5는 커널의 “지지(support)”(0이 아닌 값의 총 폭)로, Magic Kernel Sharp 2013은 −2.5에서 +2.5까지이므로 5입니다. 두 번째 인자는 생성할 이미지 파일명입니다. 생성된 mks-2013-input.png (직접 빌드할 수 없다면 링크에서 다운로드 가능)을 보면,

Magic Kernel Sharp 2013용 5×5 커널 테스트 입력 파일
어두운 회색 배경 위에 밝은 회색의 1픽셀 두께 수직선이 중앙에 있는 5×5 이미지임을 알 수 있습니다. (-h는 도움말, -H는 수직 대신 수평선.)
이제 여러분의 Magic Kernel Sharp 2013 구현으로 이 이미지를 충분히 큰 배율로 확대합니다. 예를 들어 내 참조 구현에서는:
$ resize_image mks-2013-input.png -k 100 -m MAGIC_KERNEL_SHARP_2013 mks-2013-jpc.png
로 100배 확대할 수 있습니다. 결과는 mks-2013-jpc.png입니다.

내 Magic Kernel Sharp 2013 구현으로 테스트 입력을 확대한 결과
이제 두 번째 분석 프로그램에 넣습니다.
$ analyze_kernel_test_output 5 100 mks-2013-jpc.png mks-2013-jpc.csv
여기서 확대 배율이 100임을 지정해야 했습니다. 출력 파일 mks-2013-jpc.csv에는 리사이징 프로그램이 사용한 커널을 경험적으로 계산한 값이 담깁니다. 원하는 그래프 도구로 그릴 수 있습니다.

내 Magic Kernel Sharp 2013 구현의 경험적 커널
이는 위에서 보여준 것과 시각적으로 일치합니다. 실제 공식(위)을 매우 얇은 주황색으로 이 경험적 파란색 그래프 위에 겹쳐 그리면, 커널이 정확히 구현되었음을 확인할 수 있습니다(보려면 화면을 확대해야 할 수도 있습니다).

파란 그래프 위에 올바른 커널을 매우 얇은 주황색으로 오버레이
ImageMagick의 Magic Kernel Sharp 2013 구현도 같은 방식으로 테스트할 수 있습니다. ImageMagick으로 확대를 수행합니다.
$ magick mks-2013-input.png -colorspace RGB -filter MagicKernelSharp2013 -resize 10000% -colorspace sRGB mks-2013-magick.png

ImageMagick의 Magic Kernel Sharp 2013 구현으로 테스트 입력을 확대한 결과
그리고 분석합니다.
$ analyze_kernel_test_output 5 100 mks-2013-magick.png mks-2013-magick.csv
그래프를 그리면 위와 비슷한 결과가 나옵니다.

ImageMagick 구현의 경험적 커널
한 가지 차이는 값들이 분명히 양자화(quantized)되어 있다는 점입니다. 올바른 커널과 비교하면 약간의 편차도 보입니다.

파란 그래프 위에 올바른 커널(주황)을 오버레이
나는 이것이 심각한 문제라고 생각하진 않지만, 완전히 이해하진 못합니다. 내부 기본 quantum depth가 높고, 오차 확산 디더링이 기본으로 켜져 있다면 내 구현만큼 좋은 결과가 나올 것이라 기대했기 때문입니다. 아래에서 다시 다루겠습니다.
Magic Kernel Sharp 2021도 같은 방식으로 테스트할 수 있습니다. 이 경우 지지는 9입니다.
$ make_kernel_test_input 9 mks-2021-input.png
이는 mks-2021-input.png를 생성합니다.

Magic Kernel Sharp 2021용 9×9 커널 테스트 입력 파일
$ resize_image mks-2021-input.png -k 100 -m MAGIC_KERNEL_SHARP_2021 mks-2021-jpc.png

내 Magic Kernel Sharp 2021 구현으로 테스트 입력을 확대한 결과
$ analyze_kernel_test_output 9 100 mks-2021-jpc.png mks-2021-jpc.csv
올바른 커널(주황)과의 비교로 바로 가면:

내 Magic Kernel Sharp 2021 구현(파랑) + 올바른 커널(얇은 주황) 오버레이
내 구현이 올바른 것으로 보입니다.
ImageMagick의 Magic Kernel Sharp 2021 구현도 테스트할 수 있습니다.
$ magick mks-2021-input.png -colorspace RGB -filter MagicKernelSharp2021 -resize 10000% -colorspace sRGB mks-2021-magick.png

ImageMagick의 Magic Kernel Sharp 2021 구현으로 테스트 입력을 확대한 결과
$ analyze_kernel_test_output 9 100 mks-2021-magick.png mks-2021-magick.csv
역시 올바른 커널(주황)과의 비교로 바로 가면:

ImageMagick 구현(파랑) + 올바른 커널(얇은 주황) 오버레이
화면을 확대해 주황 곡선을 보면, 이 결과는 거의 확실히 양자화가 유일한 편차 원인임을 더 명확히 가리킵니다. 위의 확대 이미지에서 양자화를 실제로 볼 수 있는데(세로 “띠”가 보임), 이는 내가 ImageMagick의 기본 quantum depth나 기본 오차 확산 디더링에 대해 이해를 잘못했음을 시사합니다.
Magic Kernel Sharp의 참조 구현은 다음 ANSI C *nix 코드(Windows는 Cygwin 사용)에 들어 있습니다.
12개의 샘플 프로그램이 포함되어 있습니다.
resize_image JPEG 또는 PNG 이미지를 리사이즈. Magic Kernel Sharp 3, 4, 5, 6 중 아무거나를 논문에 опис한 Sharp 근사와 함께 사용할 수 있으며; Magic Kernel 3, 4, 5, 6; (bi)linear 보간; 최근접; Lanczos-2 또는 -3도 지원. 추가 샤프닝 지정 가능. rotate_resize_shift_image JPEG/PNG를 회전, 리사이즈, 이동. Magic Kernel Sharp Resampler를 활용하며, resize_image의 분리 가능한(separable) 커널 리사이징보다 더 일반적이고 강력하지만 더 느림. change_image_perspective JPEG/PNG의 시선 중심 방향을 이동해 원근을 변경하고, 위 변환들을 적용. 역시 Magic Kernel Sharp Resampler 활용. blur_image Magic Blur로 블러(= Magic Kernel 3을 같은 크기 블러 커널로 사용). sharpen_image 간단한 3탭 샤프닝 필터로 이미지 샤프닝. copy_image JPEG/PNG 복사(트랜스코딩에 유용). subtract_image 두 이미지 차이를 중간 회색 기준 변동으로 표현하며, 강도 스케일을 확대할 수도 있음. 테스트에 유용. draw_magic_kernels 코드베이스의 6개 Magic Kernel 공식 구현 검증에 유용. make_gaussian_blob 논문에서 사용한 가우시안 블롭 이미지 생성. make_vertical_grate 논문에서 사용한 수직 그레이팅 이미지 생성. make_kernel_test_input 임의의 리사이징 라이브러리/앱이 실제 구현한 커널을 테스트하기 위한 이미지 생성. analyze_kernel_test_output 테스트 결과를 분석해 해당 라이브러리/앱이 구현한 실제 커널을 경험적으로 계산.
또한 84개의 유닛 테스트 및 데스 테스트 실행 파일이 제공됩니다.
빌드 방법은 압축파일 내 _README에 있습니다.
여기 제공되는 모든 코드는 내 개인 코드베이스이며, MIT-0 라이선스로 제공됩니다.
Magic Kernel Sharp를 구현하는 누구든 돕게 되어 기쁩니다. 언제든 직접 연락해 주세요.
Magic Kernel이 마음에 들었다면, 내가 수십 년 동안 퍼블릭 도메인으로 공개해온 다음 이미지 처리 리소스들도 유용할 수 있습니다.
The Magic Edge Detector Magic Kernel Sharp의 힘을 활용한 에지 검출 알고리즘. 흔한 Sobel, Scharr, Prewitt, Roberts-cross 알고리즘보다 우수(2011–2021).
UnBlock 파라미터 튜닝 없이 이미지/비디오의 “블로키(blockies)”를 제거하는 알고리즘(2005–2021).
UnBlur 위치 공간(position-space) 디블러링 알고리즘(1999–2021).
JPEG-Clear Magic Kernel Sharp를 활용한 탑다운 점진 이미지(mipmapping) 알고리즘(2006–2021).
3D JPEG-Clear JPEG-Clear를 3D 체적 데이터에 적용한 것(2010–2021).
리사이징 엔진을 처음부터 만들고, 그에 Magic Kernel Sharp 2013을 쓰고 싶다면 이 부록이 여러분을 위한 것입니다.
출력 이미지(픽셀)의 각 차원 크기를 입력 이미지의 해당 차원으로 나눈 비율을 k라 하겠습니다. 축소(리덕션)에서는 k<1, 확대(인라지)에서는 k>1입니다. 여기서는 각 방향으로 늘이기(stretch) 같은 경우는 고려하지 않지만, 필요하다면 x와 y에서 다른 k를 쓰는 것은 실무에서 자명하게 구현할 수 있습니다. 단순화를 위해 1차원만 보겠습니다. x와 y 커널은 명백히 분리 가능(separable)이므로, 각 차원에 대해 차례대로 같은 알고리즘을 반복하면 됩니다.
축소에서는 많은 입력 픽셀이 하나의 출력 픽셀에 매핑됩니다. 출력 픽셀 위치 i(정수)는 단순하게는 입력 픽셀 위치 y=i/k에 대응하지만, 일반적으로 y는 정수가 아닙니다. 예를 들어 폭 210픽셀 이미지를 21픽셀로 줄이면 k=1/10입니다. 단순하게는 출력 0이 입력 0, 출력 1이 입력 10… 출력 20이 입력 200에 대응한다고 시각화할 수 있습니다. (실제로는 픽셀 _타일_에 대해 맞는 설명이고, 픽셀의 “위치”를 타일의 _중심_으로 보므로 입력/출력 픽셀 위치에 반 픽셀 오프셋을 적용해야 합니다: y+1/2 = (i+1/2)/k. 하지만 이 예에서는 단순화를 위해 그 미묘한 bookkeeping은 무시하겠습니다. 이는 픽셀 격자의 “시작점”만 결정합니다.)
각 출력 픽셀 i에 대해 Magic Kernel m(k y−i)를 입력 이미지 위에 덮어씌웁니다. 예를 들어 i=10인 가운데 출력 위치의 경우, 커널 최대는 y=i/k=100에서 발생하며 이는 m(x)에서 x=0에 해당합니다. y<(i−3/2)/k=85에서는 0이며 이는 m(x)에서 x<−3/2에 해당합니다. y>(i+3/2)/k=115에서도 0이며 이는 x>+3/2에 해당합니다.
커널이 0이 아닌 y-공간(입력 이미지 공간)의 각 정수 위치에서, 비정규화 가중치는 커널값 m(k y−i)로 둡니다. 예를 들어 y=90에서는 m(90/10−10)=m(−1)=1/8입니다.
그 다음 모든 비정규화 가중치를 합하고, 합이 1이 되도록 정규화합니다. 이렇게 얻은 가중치 집합으로 출력 픽셀의 강도를 계산하는데, 해당 입력 픽셀 강도의 가중합입니다. (2D 이미지에서는 각 단계에서 각 출력 위치에 대한 가중치 집합은 한 번만 계산해 행/열에 재사용하면 됩니다.)
Magic Kernel로 축소가 끝나면, 결과에 단순 3탭 Sharp 2013 후처리 필터 {−1/4, +3/2, −1/4}(각 방향)를 컨볼루션하여 최종 Magic Kernel Sharp 2013 축소 이미지를 만듭니다.
확대에서는 개념적으로는 Magic Kernel Sharp 2013 커널을 적용하지만, 구현 형태는 다소 다릅니다. 이 경우 각 _입력_이 많은 출력 픽셀에 대응합니다. 따라서 Magic Kernel을 “보간 필터”로 쓰고 싶지만, 보통 수학에서 하듯 가장 가까운 두 샘플만 쓰는 대신, 세 샘플을 사용합니다(Magic Kernel의 지지가 3 단위이기 때문). 각 출력 위치에 대해 입력 공간으로 역매핑하고, 그(일반적으로 정수가 아닌) 위치에 Magic Kernel을 중심 맞춥니다. 그 커널 지지 안에 들어오는 세 입력 샘플 각각에 대해 m(x) 값을 읽어, 해당 입력 픽셀이 출력 픽셀에 기여하는 비정규화 가중치로 사용합니다.
그렇다면 Sharp 단계는? 위에서 분명히, 이는 Magic Kernel m(x)와 같은 공간에서 적용되어야 합니다. Magic Kernel과 Sharp 2013 커널의 컨볼루션이 델타 함수에 가깝다는 것이 핵심이며, 컨볼루션은 두 함수가 같은 공간에 정의될 때만 의미가 있습니다. 이 경우 그 공간은 출력 공간이 아니라 입력 공간입니다(확대에서는 입력 공간에서 m(x)를 적용했기 때문). 따라서 먼저 입력 이미지에 3탭 Sharp 2013 커널을 적용한 다음, 그 결과를 Magic Kernel로 확대해야 합니다. 이 두 연산의 결합이 Magic Kernel Sharp 2013 확대 알고리즘입니다.
Magic Kernel을 만들면서 얻은 또 다른 유용한 부산물은, Facebook 내부 여러 팀이 이미지의 블러 버전을(어떤 경우에는 매우 블러) 만들어야 했다는 점에서 나왔습니다.
나는 Magic Kernel 업사이징 커널을 블러 커널로 쓸 수 있음을 빠르게 깨달았습니다. 이 경우 원 이미지 공간에서 같은 크기 출력으로 적용합니다. 블러 양은, 표준 형태 m(x)에 비해 위치 공간 x에서 Magic Kernel을 k 배 확대해서 적용함으로써 쉽게 제어됩니다. k>1이면 대략 각 입력 픽셀이 k개의 출력 픽셀에 걸쳐 “퍼지게” 됩니다. 연속 함수 m(x)의 표준편차가 1/2이므로, 샘플된 필터의 표준편차는 대략 k/2이고, 따라서 2표준편차 폭은 대략 k 픽셀입니다.
k<1에서는 조금 더 조심해야 합니다. k→2/3이면 점근적으로 블러가 없는 상태가 되는데, k<2/3에서 스케일된 Magic Kernel의 지지가 픽셀 간격보다 작아지기 때문입니다. 이를 우회하고 모든 양의 b에 대해 의미 있는 “블러” 파라미터 b를 갖기 위해, 0<b<1에서는 (b=0, k=2/3)와 (b=1, k=1) 사이를 선형 보간하고, b>1에서는 k=b로 정의할 수 있습니다. (이 정의에서는 2표준편차 폭이 모든 양의 b에 대해 여전히 대략 b입니다.)
이 “Magic Blur” 알고리즘은 아주 작은 블러부터 매우 큰(무제한) 블러 반경까지, 최적의 품질과 부드러움으로 구현할 수 있습니다. (가우시안 블러를 더 효율적으로 수행하는 방법도 지적된 바 있습니다. Magic Blur는 기존 하드웨어 라이브러리와 호출 코드 스택을 재사용할 수 있다는 점에서 편리했습니다.)
Magic Kernel Sharp는 임의 차원의 데이터 리샘플링에 사용할 수 있습니다. 나는 한 가지 체적 파일 포맷을 예로 들어 3차원에 대해 구현했으며, JPEG-Clear의 3D 일반화 코드에 있습니다.
Eddie Edwards의 질문에 답하기 위해, 나는 Magic Kernel Sharp를 오디오 응용(사실 어떤 1차원 신호 처리에도)에 어떻게 구현할 수 있는지 살펴보았습니다. 위에서 제공한 C 코드는 Kernel 클래스를 포함하며 다차원 응용에 최적화되어 있습니다. 각 차원의 크기가 비교적 “작고”(수천 정도), 차원이(보통 2~3차원) 여러 개이므로 각 차원에서 모든 출력 위치에 대한 커널을 미리 계산해두면, 그 차원에 직교하는 하이퍼플레인 값들에 대해 여러 번 적용할 수 있어 가치가 있습니다.
이 방식은 오디오 같은 1차원에는 적합하지 않습니다. 여기서는 리사이징 비율이 유용하게 반복되는 단순한 유리수인 경우가 아니면, 각 출력 위치에 대해 커널이 한 번만 적용됩니다. 입력 크기는 사실상 무제한이며, 스트리밍 응용에서는 고정된 커널을, 미리 로드된 신호 위에서 움직이는 대신, 스트림되는 입력 신호에 통과시키는 방식이 됩니다.
그 당시 나는 이런 1차원 응용을 위한 좋은 범용 Magic Kernel Sharp 구현을 갖고 있지 않았습니다. 하지만 Eddie의 구체적 질문—48kHz와 96kHz 오디오 변환에 쓸 수 있나?—에 답하기 위해, 그 특수 케이스를 코딩했습니다.
그 이후 나는 임의의 샘플 레이트로 리샘플링할 수 있는 범용 샘플링 프로그램을 구현했습니다.
아래 코드는 16비트 PCM WAV만 다루는데, 그 포맷 래퍼가 구현하기 가장 쉬웠기 때문입니다. 하지만 코드는 완전히 일반적이며 어떤 제대로 된 오디오 처리 시스템에도 쉽게 넣을 수 있습니다.
샘플 프로그램 두 개가 포함됩니다.
resample_wav 임의의 16비트 PCM WAV 파일을 임의 샘플 레이트로 리샘플링.
wav_double_halve 이전 프로그램으로, 16비트 PCM WAV 파일의 샘플 레이트를 두 배 또는 절반으로만 바꾸며 최소 48kHz까지.
또한 68개의 유닛 테스트 및 데스 테스트 실행 파일이 제공됩니다.
빌드 방법은 압축파일 내 _README에 있습니다.
여기 제공되는 모든 코드는 내 개인 코드베이스이며, MIT-0 라이선스로 제공됩니다.
두 프로그램은 모두 v=7 Sharp 커널 근사(위 논문에서 계산한 최고의 Magic Kernel Sharp 버전)를 사용한 Magic Kernel Sharp 6을 사용하므로, Sharp 커널은 항상 15탭입니다.
반/배율 프로그램에서 Magic Kernel은 반으로 줄일 때 12탭이고, 두 배로 늘릴 때 6탭 커널이 번갈아 두 세트가 사용됩니다. 따라서 스트리밍 컨텍스트에서, 두 커널의 꼬리 때문에 제거할 수 없는 지연이 203 마이크로초입니다.
범용 프로그램은 이 “반복 커널” 방법론을 유리수인 모든 리샘플링 비율로 확장합니다(실제로는 대부분이 그렇습니다).
일반 다운샘플링에서는 새로운 이슈가 생길 수 있는데, 위의 Facebook 포스트 스레드에서 논의됩니다. Magic Kernel Sharp 커널은 수직 벽(vertical walls)이 아니라 유한한 “롤오프(roll-off)”를 갖습니다. 입력 오디오가 새로운 나이퀴스트 주파수 주변에 유의미한 신호를 갖는다면, 나이퀴스트 바로 위의 부분이 리샘플링 전에 완전히 필터링되지 않아 나이퀴스트 바로 아래로 에일리어싱될 수 있습니다. 이것이 중요한지는 응용에 달려 있습니다. Eddie의 경우 입력은 항상 오디오 범위로 사실상 로우패스 필터링되어 있었고, 리샘플링 레이트는 44.1kHz 이상이었기 때문에 문제가 아니었습니다.
이미지 응용에서는 이런 에일리어싱이 눈에 띄는 시각적 아티팩트를 대개 만들지 않습니다. 결과 에일리어싱 신호 자체가 나이퀴스트 근처에 있고 시각적으로 평균화되는 경향이 있기 때문입니다. 반면 오디오에서는 귀로 주파수를 직접 구분할 수 있어, 이런 에일리어싱이 콘텐츠/컨텍스트에 따라 해로울 수 있습니다.
따라서 범용 리샘플링 프로그램에는 Magic Kernel Sharp 필터의 대역폭을 사실상 절반으로 하는 선택적 커맨드라인 스위치가 포함되어 있습니다. 이는 첫 번째 6차 영점을 새로운 나이퀴스트 주파수에 놓으면서도, 샘플링 주파수의 배수에서 고차 영점을 유지합니다. 이렇게 하면 새로운 나이퀴스트 주파수에서 유의미한 스펙트럼 에너지를 잘 마스킹할 수 있습니다. 다만 나이퀴스트와 샘플링 주파수 사이의 유의미한 에너지는 여전히 에일리어싱될 수 있습니다. 또한 이 방법은 표준 방법보다 약 7배 느린데, Magic Kernel Sharp의 일반적인 인수분해(Magic Kernel + Sharp 단계)가 더 이상 적용되지 않고, 더 넓은 전체 Magic Kernel Sharp 커널을 큰 샘플 공간에서 적용해야 하기 때문입니다.
프로그램들은 꽤 잘 작동하는 듯합니다. 다만 논문에서는 Magic Kernel Sharp 6이 고정밀 요구를 충족할 수 있다고 말했지만, 이런 1차원 케이스를 분석해보니 어떤 응용에서는 더 높은 세대가 바람직할 수도 있다는 확신이 생깁니다. 이는 어렵지 않지만 당시에는 하지 않았습니다. 또한 논문에서 Sharp 커널에 목표로 한 8비트 정확도는, 보통 16~24비트인 오디오에는 부족해 보입니다. 다만 Sharp 커널은 첫 번째 나이퀴스트 존 내의 주파수 응답을 평탄화할 뿐이고, 안티앨리어싱 성질은 모두 Magic Kernel에 들어 있다는 점(더 높은 세대는 더 많은 dB 억제)을 기억할 가치가 있습니다. 물론 이런 개선은 제거할 수 없는 지연을 증가시킵니다. 예컨대 반/배율 사용 사례에서, Magic Kernel의 세대를 한 단계 올릴 때마다 10 마이크로초, Sharp 필터 근사를 한 단계 올릴 때마다 21 마이크로초가 추가됩니다.
위에서 말했듯, Magic Kernel Sharp 축소(2013 또는 2021)는 같은 크기 필터링과 비-안티앨리어싱 축소만 제공하는 하드웨어 가속 라이브러리로도 구현할 수 있습니다. 2013년 Facebook에서 내 구현이 그랬습니다.
먼저, 위에서 설명한 대로 Magic Kernel을 1/k 배로 스케일하되, 입력 이미지에 정규 필터로 적용합니다. (이는 원 이미지 공간에서 원 이미지를 블러 처리하지만, 축소 후 최종 출력 공간에서는 블러가 아닙니다.)
다음으로 하드웨어 라이브러리에서 उपलब्ध한 최선의 축소 방법(예: bilinear)을 적용합니다. 이 축소는 일반 이미지에 대해 제대로 안티앨리어싱되지 않을 수 있지만, Magic Kernel로 사전 블러된 이미지에는 충분합니다.
마지막으로 축소 결과에 Sharp 필터(2013 또는 2021)를 적용합니다.
대부분의 실용적 목적에서 결과는 전체 Magic Kernel Sharp 알고리즘과 구별되지 않으며, 제대로 안티앨리어싱되지 않은 하드웨어 축소를 그냥 사용하는 것보다 엄청나게 좋습니다.
이 질문은 이상해 보일 수 있습니다. 2006년에 나는 원래 “매직” 커널로 이미지의 2배 확대부터 시작했으니까요. 왜 지금 이게 중요할까요?
실용적으로는, 내 Magic Edge Detector, mipmapping 인코딩, 그리고 3D 일반화에서 반/배율 커널을 사용하기 때문에 중요합니다. 이론적 엄밀성 측면에서도, 2006년에 모든 것을 시작한 커널이 최종 형태로 어떻게 변환되는지 “루프를 닫는” 것은 가치가 있습니다.
하지만 답은 전혀 자명하지 않습니다. 원래 “매직” 커널 출력에 Sharp 2013 또는 2021을 적용하면 되는 걸까요?
그렇게 하면 이상적 결과가 아니라는 것은 쉽게 알 수 있습니다. 위에서 우리는 Sharp 커널을 (일반화된) Magic Kernel 출력에만 적용해 왔습니다. 분석이 말해주는 최적 컨볼루션이 그것입니다. 그리고 _k=2 또는 k=1/2에서의 Magic Kernel은 원래 “매직” 커널과 정확히 같지 않다_는 것도 쉽게 확인할 수 있습니다.
예를 들어 2배 확대 Magic Kernel의 경우, 관심 있는 “타일” 위치가 {−5/4, −3/4, −1/4, +1/4, +3/4, +5/4}이고 가중치는 {1, 9, 22, 22, 9, 1} /32입니다. 이는 원래 “매직” 커널의 {1, 3, 3, 1}/4 = {0, 8, 24, 24, 8, 0}/32와 미묘하게 다릅니다. 차이는 크지 않아 보일 수 있습니다(바깥 네 가중치에서 각각 1/32를 가져와 중앙 두 가중치에 모두 주었을 뿐). 하지만 위치 공간의 이런 작은 변화는, Magic Kernel Sharp(2013이든 2021이든)의 가장 “마법 같은” 성질을 주는 푸리에 공간의 고차 영점에 불균형하게 큰 영향을 줍니다.
(실제로 내 연구 논문을 읽었다면, 원래 “매직” 커널은 특별한 k=2 및 k=1/2 값에서의 선형 보간 커널, 즉 “Magic Kernel 2”일 뿐임이 분명할 것입니다. 원래 “매직” 커널로 이미지를 반복 리사이즈할 때에만 결과가 Magic Kernel에 점점 가까워집니다.)
따라서 일반적으로, k=2 또는 k=1/2에서의 전체 Magic Kernel Sharp 2021 알고리즘을 사용해 “2배/1/2” 커널을 정의해야 합니다.
위에서 Magic Kernel Sharp의 수학적 성질을 수치적으로 분석할 때 생기는 미묘한 문제 하나를 언급하겠습니다. 바로 _가장자리 효과(edge effects)_입니다.
수학적으로 커널을 정의할 때는, 압도적으로 _평행이동 불변(translation-invariant)_인 커널만 고려하는 것이 편리합니다. 즉 어디에 적용하든 커널 모양이 같아서 k(x,y)=k(x−y)이고, 어떤 신호 s(x)에 적용하면 그 불변 커널 함수 k(x)와 s(x)의 컨볼루션이 되며, 컨볼루션의 푸리에 변환은 각 푸리에 변환의 곱이라는 성질을 그대로 쓸 수 있습니다. 위의 푸리에 분석들은 모두 이 단순화를 전제합니다.
위에서 다룬 커널들이 평행이동 불변처럼 보일 수 있고, 제시한 형태로는 그렇습니다. 문제는 이미지처럼 _유한한 범위_의 샘플링 격자를 고려할 때입니다. 컨볼루션과 푸리에 분석을 위해 평행이동 불변을 유지하려면 위치 공간에서 “주기적 경계 조건(periodic boundary conditions)”을 가정해야 합니다. 즉 왼쪽 끝 픽셀의 왼쪽은 사실 오른쪽 끝 픽셀이라는 뜻입니다. 이는 수학적 푸리에 분석(이론물리)에는 아주 잘 맞습니다. 하지만 이미지 처리에서는 선택지가 아닙니다. 이미지의 왼쪽 가장자리가 오른쪽에 스며들게 할 수는 없습니다!
실제 이미지 처리에서는, 수학이 “왼쪽 끝 픽셀의 왼쪽으로 가라”고 말할 때, 그냥 왼쪽 끝 픽셀에 머뭅니다. 오른쪽 끝으로 래핑하지 않고, 그 왼쪽 끝 값에 “쌓아 올립니다(pile on)”. 이미지 밖으로 나간 이론적 픽셀 위치들은 왼쪽 끝 픽셀로 대체되고, 다른 세 변도 마찬가지입니다.
이 “쌓아 올림”이 이상한 시각적 아티팩트를 만들 것 같지만, 실제로는 거의 모든(“비병적”) 상황에서 그렇지 않습니다. 우리는 사실상 이미지를 주변 빈 공간으로 “연장”하는데, 이미지 내에 있는 가장 가까운 가장자리/코너 픽셀 값을 복사해 채운 후 필터를 적용하고, 연장된 가장자리를 잘라내는 것에 불과합니다. 이를 “연장 경계 조건(extension boundary conditions)”이라고 부를 수 있습니다.
시각적으로 연장 경계 조건은 훌륭합니다. 가능한 한 최선입니다. 하지만 수학적으로는 모든 것을 엉망으로 만듭니다.
따라서 위 커널들의 수치적 분석을 위한 유용한 작업 패러다임은 다음과 같습니다. 코드에 주기적 경계 조건과 연장 경계 조건을 선택하는 플래그를 둡니다. 푸리에 성질, 커널 합성 등 수학적 성질 분석에는 주기적 경계 조건을 사용합니다. 실제 이미지 응용에는 연장 경계 조건을 사용합니다.
이것은 또한, Magic Kernel Sharp 2021 커널을 실무에서 구현할 때, (1) 두 번의 커널 적용(Magic Kernel 후 Sharp 2021)으로 정의하느냐, (2) 단일 커널(두 커널 합성)로 정의하느냐에 따라 아주 미세한 차이가 생길 수 있음을 뜻합니다. 주기적 경계 조건에서는 두 구현이 동일해야 하지만(아래 참조), 연장 경계 조건에서는 각 커널 적용의 가장자리 효과 때문에 두 연산이 동일하지 않습니다. 물론 시각적으로는 무시할 수준입니다. 다만, 아래 참조 구현처럼 커널 구현의 정확성을 확인하는 유닛 테스트를 만들려는 경우에는 염두에 두어야 합니다.
또 다른 복잡성은, 두 커널을 합성할 때 각각을 정규화한 뒤 합성하고, 합성 결과도 다시 정규화하는 경우입니다. (커널 빌더 클래스가 생성한 커널을 자동 정규화한다면 쉽게 이런 일이 생깁니다.) 특별한 k 값이 아닌 한, Magic Kernel의 원시 가중치 정규화는 모든 출력 위치에서 정확히 같지 않고, 정규화 단계가 이를 고정합니다. 하지만 정규화와 합성은 교환되지 않으므로, 정규화 후 Sharp 2021과 합성한 결과는, 정규화되지 않은 커널을 Sharp 2021과 합성한 뒤 마지막에 정규화한 결과와 아주 약간 다릅니다. 역시 실용적으로는 무시할 수준이지만, 구성 가능한 유닛 테스트에는 영향을 줍니다.
이 페이지는 내가 2006년부터 수행해온 개인 취미 연구를 설명합니다. 여기의 모든 의견은 나 개인의 것입니다. 나는 2011년 초 이 페이지(및 이전 도메인의 전신 페이지)를 통해 Magic Kernel을 퍼블릭 도메인으로 공개했습니다. 또한 지적된 바처럼, 이것과 이후의 샤프닝 단계는 cardinal B-spline의 일반 이론 안에 모두 포함되며, Magic Kernel Sharp가 선행기술(prior art)에 포함되어 특허 대상이 아님을 명시적으로 확인합니다. 여기 제공되는 모든 코드는 내 개인 코드베이스이며 MIT-0 라이선스로 제공됩니다.
©2006–2025 John Costella