Linalg 방언의 설계 원칙, 선행 사례로부터의 교훈, 핵심 관찰, 그리고 MLIR에서 코드 생성 친화적 고수준 연산과 변환을 위한 접근을 설명한다.
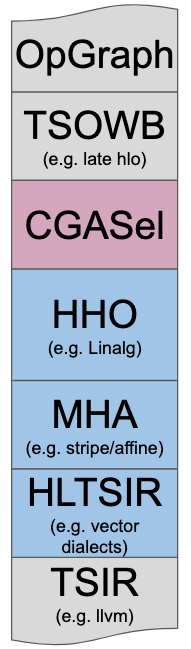이 문서는 Linalg의 기존 구현으로 이어진 핵심 설계 원칙을 설명하고, 코드 생성을 촉진하기 위한 보다 고수준의 중간 표현(IR)과 방언(Dialect)을 구축할 때 수반되는 트레이드오프를 드러내는 것을 목표로 한다. MLIR에서의 코드 생성(codegen)을 설명하는 단순화된 스키마를 고려해보자. Linalg는 고수준 계층적 최적화(HHO 상자)를 해결하고, 전문가 컴파일러 조합 환경(Mixture Of Expert Compilers, 즉 CGSel 상자)과 원활히 상호 운용되도록 설계되었다. 이 작업은 이 분야의 풍부한 선행 사례에서 영감을 받았으며, 그로부터 핵심 교훈을 얻고자 한다. 이러한 문서화와 성찰 노력은 또한 고수준 Tensor Compute Primitive 방언 및 변환의 개발을 논의하기 위한 워킹 그룹 제안의 맥락에도 놓여 있다. 우리는 선행 사례의 교훈, 본 문서에 제시된 설계 원칙, 그리고 Linalg의 아키텍처가 커뮤니티가 이러한 고수준 텐서 연산 프리미티브를 정의하는 경로를 정립하는 데 도움이 되기를 바란다.
Linalg는 MLIR에서 코드 생성을 부트스트랩하기 위한 실용적 방언으로 출발했다. 정확한 의존성 분석이나 다면체 코드 생성 같은 복잡한 문제를 “정의로 없애버리고(defining away)”, 가능할 때 빠른 라이브러리 구현을 호출할 수 있는 능력을 도입함으로써다. Linalg는 연산과 변환을 선언적으로 정의하며, 원래는 pointwise, matmul, conv 등과 같은 선형대수 유사 의미론을 가진 연산으로 제한되었다. 이 접근은 컴파일러 최적화와 효율적인 라이브러리 구현을 모두 활용하여 고수준 생산성-우선의 코드 생성 솔루션을 구축할 수 있게 한다. 예를 들어, 특정 HPC 라이브러리나 ISA에 어떤 메모리에 저장된 피연산자에 대해 달성 가능한 피크 성능의 95%로 실행되는 matmul 프리미티브가 있다면, 가능할 때는 그 프리미티브를 사용하고, 그렇지 않은 경우에는 코드를 생성할 수 있어야 한다.
그러나 Linalg의 설계가 MLIR의 설계와 함께 공진화함에 따라, Linalg가 조밀한 텐서에서의 기계학습을 넘어 더 큰 응용 도메인으로 확장될 수 있음이 분명해졌다.
Linalg의 설계와 진화는 IR과 변환이 보조를 맞추는 코드 생성 친화적(codegen-friendly) 접근을 따른다. 핵심 아이디어는 연산의 의미론이 전통적으로 컴파일러 분석으로부터 얻어지던 정보를 선언하고 운반한다는 것이다. 이 정보는 변환의 합법성 및 적용 가능성을 포착하며, 루프나 CFG 형태로 너무 일찍 낮춰(lowering) 버리면 사라지지 않는다. 핵심 변환들은 이 정보를 필요한 동안 보존하도록 설계된다. 예를 들어, 타일링과 퓨전을 거친 뒤에도 linalg.matmul은 여전히 linalg.matmul로 남는다.
또한 Linalg는 변환의 타당성(validity)을 수익성(profitability) 고려에서 분리하며, 후자는 1차 반복(iteration)에서는 의도적으로 제쳐둔다(탐색에의 적합성 설계 원칙 참조).
이 아이디어의 첫 구현은 EuroLLVM 2019 개발자 회의에서 첫 번째 MLIR 튜토리얼의 Linalg 섹션 일부로 예시와 함께 발표되었다.
초기 구현 이후, 설계는 Regions, OpInterfaces, ODS, Declarative Rewrite Rules 등을 사용하도록 핵심 MLIR 인프라의 진화를 이끌기도 하고 함께 진화해왔다. Linalg가 채택한 접근은 StructuredOps 추상화로 확장되었으며, Linalg는 텐서와 버퍼 위의 그 구현체가 되었다. 이는 Vector 방언으로 보완되며, Linalg와 동일한 근거와 설계 원칙을 따르는 벡터 위의 구조화된 연산을 정의한다(벡터 방언은 다차원 벡터 위의 고수준 연산을 포함하고, 1차원 벡터로의 낮춤을 추상화한다).
Linalg 방언 자체는 선형대수 유사 연산을 넘어 더 표현력이 풍부해졌는데, 특히 임의의 MLIR region 주위에서 병렬성, 축소(reduction), 슬라이딩 윈도우를 지원하는 루프 둥지(loop nest)의 추상화를 제공한다는 점에서 그렇다. 또한 희소(sparse) 및 래깅(ragged) 텐서와 버퍼 같은 더 풍부한 데이터 타입을 지원하도록, 조밀(dense) 선형대수를 넘어 성장할 잠재력도 가지고 있다.
Linalg 설계는 다른 방언과 접근과의 진화 및 교류(cross-pollination)에 열려 있다. 이는 코드 생성 관련 추상화의 발상지로 성공적으로 사용되어 다음과 같은 일반화를 파생시켰다:
!linalg.view 타입은 “Strided MemRef” 타입으로 접어 넣었다.linalg.view와 linalg.subview 연산은 표준 방언으로 진화했다.linalg.for, linalg.load, linalg.store 연산은 구조화된 제어 흐름 방언(‘LoopOps’라 명명된)의 전주곡으로 진화했다. 새 사용처나 요구사항이 생기면 더 많은 구성 요소를 추출하고, 재설계하며, 일반화할 수 있다.Linalg에는 여전히 몇 가지 설계 질문이 열려 있으며, 모든 컴파일 문제에 대한 일반 해답을 주장하지는 않는다. 다만 프로그래머의 의도를 매우 고수준에서 직접 IR에 담아낼 수 있는 도메인 특화 추상화의 사고와 구현을 이끌고자 한다.
적용 범위의 진화에 비추어 보면, “Linalg”보다 더 나은 이름이 방언(및 그 근저의 접근), 그 목표와 한계에 관한 일부 혼란을 해소할 수 있을 것이다.
Linalg는 수십 년의 선행 사례에서 영감을 받아 현대적이고 실용적인 해법을 설계했다. 다음의 불완전 목록은 Linalg 설계에 영향을 준 일부 프로젝트를 가리킨다:
또한 다음 도구들에 대한 경험은, 사용자 상단부터 하드웨어 하단까지 모든 구성 요소가 상호 작용하는 방식을 총체적으로 사고하는 데 매우 유용했다:
MLIR 코드베이스의 새로움과 전례 없는 추상화 정의/혼합 지원은, 선행 사례의 성공 요소를 반영하고 통합하며 코드 생성 영역의 흔한 함정을 피할 수 있게 한다. 따라서 기존 해법 채택의 함의에 관한 논의로 흩어지기보다, Linalg는 이들 모두를 토대로 삼아 경험에서 배우고, 후견지명(hindsight)의 이점을 활용할 수 있었다.
다음의 선행 사례에 대한 성찰은 Linalg 설계에 영향을 주었다. 논의는 결코 완전하지 않지만, Linalg의 핵심 동기를 포착한다.
ONNX는 머신러닝 워크로드에 등장하는 연산들의 명세(specification)다. 따라서 주로 ML의 표현력 요구에 의해 주도되며, HPC 코드 생성을 위한 IR 설계 고려는 덜하다.
ONNX와 유사하게, Linalg는 “의미가 부여된(semantically charged)” 이름 붙은 연산들을 정의한다. 하지만 Linalg는 이러한 연산들에 대한 변환 또한 핵심 구성 요소로 보고, 필요하다면 표현력보다 변환을 우선시하며 변환을 지원하도록 IR을 정의한다.
Linalg가 추가로 다루고자 하는 바:
LIFT는 함수형 추상화에 기반하여 계산 커널을 작성하는 시스템이다. 변환은 IR에 추가 노드로 표현되며, 그 의미론은 알고리즘 수준(예: partialReduce)에 있다. LIFT는 이러한 추가 노드를 함수형 추상화에 직접 내장하는 로컬 재작성 규칙을 사용해 변환을 적용하고 합성한다.
LIFT와 유사하게, Linalg는 MLIR의 선언적 재작성 규칙 메커니즘으로 구현된 로컬 재작성 규칙을 사용한다.
Linalg는 다음과 같이 LIFT 접근을 토대로 하면서 관심사의 분리를 돕는다:
LIFT는 Linalg가 진화함에 따라 설계에 더 큰 영향을 줄 것으로 기대된다. 특히 비조밀 텐서를 지원하도록 데이터 구조 추상화를 확장할 때, 희소 및 위치 의존 배열에 대한 LIFT 추상화의 경험을 활용할 수 있다.
XLA는 Theano 이후 등장한 초기 ML 컴파일러 중 하나로, TensorFlow를 위한 실용적 컴파일 해법으로 도입되었다. Google의 xPU 하드웨어에서 빛을 발하며 중요한 퍼즐 조각이다. 특히 (1) 스칼라와 벡터 세계 사이를 오가며 코드 변환, (2) 호스트와 디바이스 코드를 모두 다루기 위한 함수 경계 넘기, (3) 에너지 효율적 xPU가 부과하는 엄격한 요구사항 준수가 뛰어나다. XLA는 강력한 conv와 matmul 연산에서 출발해, 각 연산의 의미론에 대해 컴파일러가 완전한 지식을 갖는 실용적 설계 과정을 따랐다. XLA 변환은 C++ 함수로서 합성되는 emitter를 작성하는 것으로 구성된다. 완전한 연산 의미론 지식에는 두 가지 큰 이점이 있다: (1) 변환이 본질적으로 정확하다 (2) 까다로운 xPU 타깃에서 매우 강력한 성능을 낸다.
이와 유사하게, Linalg 연산은 “자신의 의미론을 알고” “자신을 어떻게 변환·낮춤할지 안다”. 그러나 이 정보가 MLIR에서 제공되고 사용되는 방식은 매우 다르다.
Linalg가 추가로 다루고자 하는 바:
Halide는 C++에 내장된 DSL로, HalideIR을 메타프로그래밍하고 변환을 선언적으로 적용해 전문가 사용자가 프로그램을 맞춤 최적화할 수 있게 한다. Halide는 초기에는 SIGGRAPH 커뮤니티를 겨냥했으나 이제는 더 일반적으로 적용된다. TVM은 HalideIR을 기반으로 기계학습과 심층신경망 영역으로 Halide를 확장한 것이다.
Halide의 변환 방법론은 URUK와 CHiLL 컴파일러 변환 프레임워크와 유사한 원칙을 따르되, 다면체 모델의 강점(및 특히 그 복잡성)은 갖지 않는다.
Halide는 폴리헤드럴 도구가 여전히 Ω(1-10) 사용자에게만 접근 가능한 시기에, HPC 변환 방법론을 Ω(10-100) 사용자에게 접근 가능하게 만든 점이 특히 빛난다. Halide는 MLIR에서도 매우 보편적인 정규화 규칙을 적극 활용한다.
Linalg가 추가로 다루고자 하는 바:
Tensor Comprehensions는 아인슈타인 표기법을 일반화한 문법으로 텐서 연산을 표현하는 고수준 언어이며, 효율적인 GPU 코드로 낮추는 종단 간 컴파일 플로우를 제공한다. Caffe2와 PyTorch 두 개의 ML 프레임워크에 통합되었다.
컴파일 플로우는 Halide와 ISL에서 파생된 다면체 컴파일러를 결합하고, HalideIR과 ISL의 스케줄-트리 IR을 모두 사용한다. 컴파일러는 다면체 컴파일 알고리즘 모음을 제공해 퓨전을 수행하고, 다단계 병렬성과 메모리 계층의 더 깊은 수준으로의 승격을 선호한다. Tensor Comprehensions는 몇 개의 사전 정의된 전략을 매개변수화 변환과 튜닝 노브로 고정하기만 해도 훌륭한 결과를 제공할 수 있음을 보였다. 그 이전 작업에서는 간단한 유전적 탐색과 자동 튜닝 프레임워크만으로도 비-계산 한계(regime)에서 좋은 구현을 찾기에 충분했다. 이는 다양한 변환으로 얻을 수 있는 코드 버전이 루프라인 한계에 근접하는 버전을 포함해야 함을 요구한다. Tensor Comprehensions의 궁극적 목표는 Halide 고수준 변환과 다면체 중간 수준 변환을 실질적으로 혼합하여, 두 스타일의 컴파일을 모두 활용할 수 있는 실용 시스템을 구축하는 것이었다.
Linalg가 추가로 다루고자 하는 바:
이들 중 많은 문제는 MLIR 인프라에 이러한 아이디어를 구현함으로써 자연스럽게 해결된다.
다면체 모델은 수십 년에 걸쳐 루프 수준 최적화의 최전선에 있었으며, GRAPHITE(GCC), Polly(LLVM)와 같은 프로덕션 컴파일러에 여러 구현이 있다. PolyMage, Tensor Comprehensions 같은 도메인 특화 언어에서 효율적인 코드를 생성하는 데는 결정적이었지만, 범용 최적화 파이프라인에는 완전히 포함되지 못했다. 다면체 변환의 역할에 대한 상세 분석은 MLIR의 태동 시기로 거슬러 올라가는 simplified polyhedral form 문서에 제공된다.
특히, 다면체 추상화는 다음 이유들로 더 전통적인 컴파일러와 통합하기가 도전적이었다.
MLIR의 Affine 방언은 위의 통합 문제를 해결하도록 특별히 설계되었다. 특히, 변환 전 과정에서 동일한 형태(IR의 루프, 다만 경계 표현 방식에 제약을 추가)로 IR을 유지하여, 급격히 다른 표현 간의 일회성 변환 필요성을 줄인다. 또한 MLIR region을 사용해 SSA 형태에 다면체 표현을 내장하고, 다면체 및 SSA 기반 변환을 결합할 수 있게 한다.
MLIR의 Affine 방언은 다면체 추상화를 전통적 SSA 표현에 더 가깝게 가져온다. 위에서 설명한 오랜 통합 과제를 해결하며, C 언어 수준 추상화에서 컴파일할 때 더 적합할 가능성이 크다.
MLIR은 머신러닝 워크로드 등 C보다 더 고수준 추상화에서 시작할 수 있게 한다. 이런 경우, DSL 컴파일러와 유사하게 더 높은 수준의 추상화에서 이용 가능한 정보를 활용해, 다면체 변환에 필요한 복잡한 분석(루프 간 반복을 가로지르는 데이터 플로 분석은 지수 복잡도)을 피할 수 있다. Linalg는 가능한 경우 이 정보를 사용하고, 변환의 합법성을 연산 의미론에 통합하여 “구성상으로(by construction)” 보장하려 한다(예: 루프 타일링은 행렬 곱셈을 계산하는 루프 둥지에 적용할 수 있으며, 이를 추가로 점검하기 위해 affine 의존성 분석에 의존할 필요가 없다). 이러한 정보는 Affine 방언에는 즉시 이용 가능하지 않으며, 잠재적으로 비용이 큰 패턴 매칭 알고리즘으로만 도출할 수 있다.
다면체 컴파일 실무 경험, 특히 Affine 방언과 관련된 경험에 비추어 Linalg는 다음과 같이 결정한다.
memref 추상화를 활용하는 버퍼에 대한 view를 만든다. 이러한 view는 합성 가능하며 접근 식의 복잡성은 예측 가능하게 유지된다.이러한 선택을 고려할 때, Linalg는 입력 표현에 훨씬 더 많은 정보가 즉시 이용 가능하며 다른 추상화로 낮추기 전에 이를 활용해야 하는 고수준 컴파일에 더 적합하다. Affine은 중간 수준 변환을 위한 강력한 추상화로 남아 있으며, Linalg의 낮춤 대상로 사용되어 더 많은 변환과 의미 부하가 큰 입력과 저수준 입력의 결합을 가능하게 한다. 따라서 Linalg는 Affine을 대체하기보다 보완하는 것을 목표로 한다.
Linalg IR과 그 연산의 목적은 주로 다음과 같다:
당면 문제는 본질적으로 고성능 및 병렬 하드웨어 아키텍처를 위한 도메인 특화 워크로드의 컴파일에 의해 주도된다: 이는 HPC 컴파일 문제다.
관련 변환의 선택은 공동 설계 접근을 따르며 다음을 고려한다:
확장을 남발하고 중복을 피하려면 체계적이어야 한다. 주어진 변환은 여러 추상화 수준에 존재할 수 있지만, “수준 Y에서 변환 X를 쓸 수 있다”는 사실이 “그래야 한다”를 의미하지는 않는다. 여기서 기존 시스템의 평가와 그 강·약점의 인지가 중요하다: 단순성과 유지보수성은 1급 관심사가 되어야 한다. 이러한 추가 성찰 노력이 없다면 설계는 시간의 시험을 견디지 못한다. 동시에 복잡성은 떨쳐내기 매우 어렵다. 복잡성을 겪어보아야 한 걸음 물러서서 추상화를 재고할 동기가 생기는 듯하다.
이는 단지 시스템 Y에서 아이디어 X를 재구현하는 것이 아니다: 단순성은 이러한 성찰 노력의 결과여야 한다.
지난 20년간 제한된 응용 도메인에서 큰 성공을 거둔 DSL이 폭증했다. 이들 시스템의 주요 공통점은 CFG나 루프보다 훨씬 풍부한 구조적 정보를 사용한다는 점이다. 그럼에도 또 다른 공통점은 LLVM으로 매우 빨리 낮추고, 하나의 단계에서 넓은 추상화 간극을 넘어선다는 점이다. 이 과정은 의미 정보를 종종 떨어뜨려, 나중에 다시 재구성해야 하거나 돌이킬 수 없이 잃기도 한다.
이러한 관찰과 MLIR의 다중 추상화 수준 IR 정의 적합성은 다음 두 원칙으로 이어진다.
컴파일러 변환은 정적 구조 정보(예: 루프 둥지, 기본 블록 그래프, 순수 함수 등)를 필요로 한다. 그 구조 정보가 사라지면 재구성해야 한다.
이 현상의 좋은 예시가 다면체 컴파일러에서의 ‘올리기(raising)’ 개념이다: 여러 다면체 도구는 단순화된 C 형태나 SSA IR에서 루프 변환에 더 적합한 고수준 표현으로 올리면서 시작한다.
고급 다면체 컴파일러에서는 BLAS 변형을 비롯한 특정 패턴을 탐지하기 위한 두 번째 유형의 올리기가 존재할 수 있다. 이러한 패턴은 변환에 의해 깨질 수 있어, 탐지가 매우 취약해지거나 불가능(잘못됨)해진다.
MLIR은 region과 attribute를 사용하여 연산 의미론을 선언적으로 정의하기 쉽게 만든다. 이는 사용자 의도를 적절한 추상화에 직접 전달하는 새로운 추상화를 정의하기에 이상적 기회다.
Affine, 일반 루프 또는 CFG 형태로 너무 빨리 낮추면 변환을 도출하는 데 이용 가능한 구조의 양이 줄어든다. 루프를 다루는 것은 특정 변환 계층에 대해 CFG에 비해 순이익이지만, 중요한 정보(예: 병렬 루프, 루프 둥지를 외부 구현에 매핑하는 정보 등)는 여전히 사라진다.
이는 비자명한 단계 순서 문제를 만든다. 예컨대 루프 퓨전은 BLAS 패턴을 탐지할 능력을 쉽게 파괴할 수 있다. 가능한 한 가지 대안은 루프 퓨전, 타일링, 타일 내 루프 분배를 수행한 다음 BLAS 패턴을 탐지하기를 바라는 것이다. 이러한 스킴은 어려운 단계 순서 제약을 제시하며, 다른 결정과 패스에 간섭할 가능성이 높다. 대신, 특정 Linalg 연산은 타일링과 퓨전 같은 변환 전반에서 고수준 정보를 유지하도록 설계되었다.
MLIR은 점진적 낮춤을 위한 인프라로 설계되었다. Linalg는 이 개념을 완전히 수용하며, 코드 생성을 ‘퍼텐셜 함수(잠재 함수)를 줄이는’ 관점으로 본다. 그 퍼텐셜 함수는 특정 Linalg 연산 내 저수준 명령 수(즉 Linalg 연산이 얼마나 무겁거나 가벼운가)로 느슨하게 정의된다. Linalg 기반 코드 생성과 변환은 고수준 IR 연산과 방언에서 시작한다. 이후 각 변환 적용은 더 저수준 IR 연산과 더 작은 Linalg 연산을 도입함으로써 퍼텐셜을 줄인다. 이는 Loops + VectorOps 및 LLVMIR에 이르기까지 퍼텐셜을 단계적으로 줄인다.
핵심 Linalg 연산 집합은 네 가지 형태를 갖는다:
linalg.generic로 표현되며, 모든 완전 중첩 루프 연산을 인코딩할 수 있다.linalg.contract와 linalg.elementwise는 linalg.generic의 더 고수준 의미론을 인코딩하면서도, 속성과 문법을 통해 여러 ‘이름 붙은’ 연산을 표현한다. 향후 다른 범주 연산(예: linalg.convolution, linalg.pooling)도 계획되어 있다.linalg.matmul, linalg.add 등. 단일 범주 또는 일반 형태로 변환될 수 있는 모든 이름 형태, 즉 완전 중첩이다.linalg.softmax와 winograd 변형. 이들 연산은 완전 중첩이 아니며, (여러 방언의) 다른 연산 목록으로 변환된다.형태 간 상관관계는 다음과 같다:
+ generic
\__ + category
\__ + named
+ composite
category와 named 형태는 linalg.generic에서 파생되며 동등하다. named 연산을 category로, 이를 다시 generic으로, 그리고 다시 named로 변환할 수 있어야 한다. 다만, 해당하는 named 형태가 없다면 generic을 named로 변환할 수 없을 수 있다.
composite 연산은 다른 세 클래스/형태로 변환될 수 없고, 자체 하위 집합을 이룬다. 하지만 전개(expand) 시 다른 Linalg 형태를 사용할 수 있다. 연산 그래프를 패턴 매칭하여 composite 연산으로 변환하는 변환도 있을 수 있다.
Linalg 방언의 다양한 형태는 패턴 매칭(단일 연산 또는 DAG)을 촉진하고, 서로 다른 변환에 대해 서로 다른 형태를 정준(canonical)으로 간주할 수 있게 하려는 의도다.
Linalg의 다양한 형태는 정보도 담고 있으며, 그러한 정보는 점진적 낮춤 동안 가능한 한 보존되어야 한다. matmul 연산은 contract 연산의 특수 경우이며, 이는 다시 generic 연산의 특수 경우다. Linalg 연산(임의 형태) 위의 변환은 여전히 Linalg 연산으로 표현할 수 있다면, 가능하면 원래 형태로 분해(루프 + 산술)하는 것을 피해야 한다.
여러(종종 교환 가능한) 형태가 있고 변환의 단순함을 염두에 둘 때, 컴파일러는 매칭과 치환의 복잡성을 가능한 한 줄여야 한다. 복잡한 패턴으로 단일 연산을 매칭할 때는, generic 연산 하나에 모든 정보가 모여 있는 것이 유용하여, 서로 다른 패턴을 차례로 반복적으로 매칭할 수 있다. 그러나 패턴을 구성하기 위해 연산의 DAG를 조립할 때는, 일반 대응물보다 max + div + reduce + broadcast 같은 이름 붙은 연산을 대상으로 매칭하는 것이 훨씬 간단하다.
여기서 형태의 상호 교환성이 유용해진다. Linalg는 특정 변환 유형에 더 쉬운 형태로 IR을 변환하기 위해 특수화와 일반화를 수행할 수 있다. 형태가 의미론적으로 동등하므로, 각 변환의 필요에 맞춰 다양한 변환 전반에 걸쳐 앞뒤로 전환할 수 있다. 해당 변환에 대해 그러한 형태를 정준으로 간주할 수 있으며, 따라서 패턴이 매칭되기를 ‘기대’할 수 있다. 이는 패턴 매처의 복잡성을 줄이고 컴파일러 파이프라인을 단순화한다.
복잡하고 영향력 있는 변환이 꼭 다루기, 작성, 유지보수하기 어려울 필요는 없다. XLA 스타일의 고수준 연산 의미론 지식을 MLIR에 직접, 이러한 의미론을 설명하는 일반 속성과 혼합하는 것은 유망한 방법이다.
컴파일러 휴리스틱은 수작업으로 만든 인간 공학적 특성이다: 이는 머신러닝 기법으로 전복(disruption)되기 알맞다. 탐색을 가능하게 하려면, 컴파일러 변환은 미세하고(fine-grained), 합성 가능하며, 그 동작을 수정할 수 있는 튜닝 파라미터를 노출해야 한다. 이는 Tensor Comprehensions에서의 이전 경험의 교훈이 이끈다.
물론 스택 전반에 즉시 ML을 쓰자고 주장하는 것은 아니다: 저수준 컴파일과 머신 모델은 LLVM에서 여전히 매우 성능이 좋다. 그러나 고수준과 중간 수준 최적화 문제에서는 모델이 저수준 컴파일러(블랙박스처럼 동작함)에 조건화(확률적으로)되어야 한다. 이러한 이유로 우리는 비용 모델을 구축하기보다 탐색 친화적 속성을 갖춘 IR과 변환 설계를 우선시한다. 그렇다고 Linalg가 비용 모델을 거부한다는 뜻은 아니다: 대신 ML 기반 기법으로 비용 모델을 자동 구축할 수 있게 하는 인프라에 투자하기를 선호한다.
MLIR은 구조화된 제어 흐름과 구조화된 데이터 타입을 위한 IR 정의를 허용한다. 우리는 위에서 설명한 이유로 이러한 속성을 활용하기로 한다. 특히 MemRefType은 조밀하지만 비연속적인 메모리 영역을 표현한다. 이 구조는 단순 조밀 데이터 타입을 넘어 확장되어, 래깅, 희소, 혼합 조밀/희소 텐서뿐 아니라 트리, 해시 테이블, 레코드 테이블, 심지어 그래프에도 일반화되어야 한다.
이처럼 더 발전된 데이터 타입에 대해서는, 데이터 구조를 순회하는 데 필요한 제어 흐름, 종료 조건 등이 정적으로 분석하고 특성화하기 훨씬 덜 간단하다. 그 결과, 런타임 적응 계산으로 진화할 가능성이 있는 해법을 설계해야 한다(예: 검사자-실행자(inspector-executor)에서 검사자가 런타임에 데이터에 대한 저비용 분석을 수행하여 실행자가 어떻게 실행해야 하는지 구성). 오늘날 MLIR에서 이러한 문제를 해결하는 구체적 해법은 없지만, 완벽한 정적 지식과 분석이 이러한 문제의 진지한 경쟁자가 되지 못할 것임은 분명하다.
다음 핵심 관찰은 Linalg 설계에 영향을 주었고, MLIR 기반 구현을 만들 때의 실제 요구와 핵심 설계 원칙을 조화시키는 데 도움이 되었다.
이는 Niklaus Wirth의 정식에 약간의 변형을 가한 것이지만, Linalg 설계의 본질을 포착한다: 제어 흐름은 데이터와 독립적으로 공중에 떠 있지 않는다. 그 반대로, 제어 흐름과 데이터 구조 사이에는 매우 강한 관계가 있으며, 둘은 서로 없이는 존재할 수 없다. 이는 Linalg 연산의 의미론과 그 변환에 여러 함의를 갖는다. 특히, 다음에 영향을 준다: 어떤 변환을 수행하는 것이 더 나은가 — 제어 흐름 조작으로서인가, 데이터 구조 조작으로서인가; Linalg 연산 속성에서인가, 일부 부분 낮춤이 발생한 후 루프에서인가; 새로운 연산 또는 속성의 관점에서 Linalg 방언의 확장으로서인가.
이는 아마 가장 놀랍고 직관에 반하는 관찰일 것이다. 변환을 위한 IR을 설계할 때, 닫힘성(closed-ness)은 종종 협상 불가능한 속성이다. 이는 URUK 및 ISL 기반 IR 같은 다면체 IR의 핵심 설계 원칙이다: 이들은 어파인 변환에 대해 닫혀 있다. MLIR에서는 여러 방언이 공존하며 일관된 전체를 이룬다. 다양한 대안을 실험한 끝에, 엄격한 방언의 닫힘성은 필요하지 않으며 완화될 수 있음이 분명해졌다. 이전 시스템에는 새로운 IR을 구축할 단순하고 원칙적인 수단이 없었고 이 제약에 시달렸을 가능성이 있다. 우리는 이것이 IR이 변환에 대해 닫혀 있어야 했던 핵심 이유라고 추정한다.
Linalg 연산은 완전 중첩 의미론만 허용하지만, 타일링과 퓨전이 시작되면 점진적으로 불완전 중첩 루프가 도입된다. 다시 말해, 불완전 중첩 제어 흐름은 “핵심 변환을 적용한 결과”로 나타난다.
점진적 낮춤에서 설명한 ‘퍼텐셜’을 고려하면, 변환에 대한 닫힘성은 퍼텐셜이 일정하게 남아 있어야 함을 함축한다. 반대로, Linalg는 변환에 대한 ‘단조성(monotonicity)’을 옹호한다.
마지막으로, 선행 사례에서의 교훈을 핵심 설계 원칙의 렌즈로 보았을 때의 관찰을 다음 그림으로 요약한다.
이 그림은 완벽히 정확하기보다는, 코드 생성 친화적 관점에서 기존 시스템에서 구조적 정보가 어떻게 분포하는지에 관한 대략적 지도를 의도한다. 놀랍지 않게도, Linalg 방언과 그 미래의 진화는 이 지도 우상단의 위치를 지향한다.