brainfuck 프로그래밍 언어를 위한 주요 컴파일러 최적화 기법들을 소개하고, 여러 비(非)자명한 brainfuck 프로그램에서 실행 시간에 어떤 영향을 미치는지 측정한다.
← brainfuck로 java를 컴파일하기헤드라인에 대한 베터리지의 법칙은 맞는가? →
Mats Linander
2015-01-07 - 뉴욕
거의 모든 계산에서, 과정들의 연속에 대한 배치는 매우 다양한 방식으로 가능하며, 계산 엔진의 목적을 위해 그중 무엇을 선택할지에는 여러 고려 사항이 영향을 미친다. 필수적인 목표 중 하나는 계산을 완료하는 데 필요한 시간을 최소로 줄이는 데 도움이 되는 배치를 선택하는 것이다.
Ada Lovelace, 1843
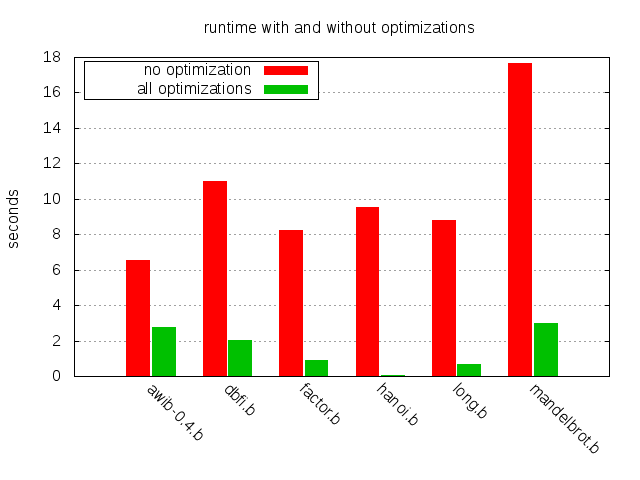
러브레이스의 말은 거의 두 세기가 지난 지금도 여전히 유효하다. 그 배치를 선택 하는 한 가지 방법은 최적화 컴파일러를 사용하는 것이다. 이 글에서는 brainfuck 프로그래밍 언어를 위한 중요한 컴파일러 최적화 전략 몇 가지를 살펴보고, 그것들이 몇 개의 비(非)자명한 brainfuck 프로그램들의 실행 시간에 어떤 영향을 미치는지 살펴본다. 아래 차트는 다룰 기법들의 영향을 보여준다.
brainfuck 프로그래밍 언어가 처음이라면, 이전 글로 가서 언어의 기본과 brainfuck으로 작성한 brainfuck-to-java 컴파일러를 만들 때 마주치는 이슈들을 확인하길 바란다. 그렇긴 해도, 이 글의 대부분은 언어 경험이 없어도 이해할 수 있을 것이다.
서로 다른 최적화 기법들의 영향도를 의미 있게 평가하려면, 최적화가 말이 될 정도로 충분히 비(非)자명한 brainfuck 프로그램 집합이 필요하다. 놀랍지 않게도, 세상에 있는 대부분의 brainfuck 프로그램은 꽤나 사소하지만 예외도 있다. 이 글에서는 그런 프로그램 6개를 살펴본다.
관심 있는 독자는 이 프로그램들에 대한 더 자세한 설명을 위해 이 저장소로 가보길 바란다.
첫 단계는 옵티마이저가 동작할 수 있는 중간 표현(IR)을 정의하는 것이다. IR로 작업하면 플랫폼 독립적인 최적화가 가능하고, brainfuck 자체보다 더 높은 표현력을 얻는다. IR이 어떻게 동작하는지 더 잘 보여주기 위해, 각 연산에 대한 C 구현도 함께 제공한다.
아래 표에는 8개의 brainfuck 명령어 전체와, 각 IR 대응물, 그리고 IR의 C 구현이 있다. 이 기본 매핑은 brainfuck를 컴파일하는 매우 단순하고 다소 순진한 방법을 제공한다.
| BF | IR | C |
|---|---|---|
+ | Add | mem[p]++; |
- | Sub | mem[p]--; |
> | Right | p++; |
< | Left | p--; |
. | Out | putchar(mem[p]); |
, | In | mem[p] = getchar(); |
[ | Open | while(mem[p]) { |
] | Close | } |
이 C 코드는 메모리 영역과 포인터가 적절히 준비되어 있다는 가정에 의존한다. 예를 들면 다음과 같다:
char mem[65536] = {0};
int p = 0;
이 시점에서 IR은 brainfuck 자체보다 더 표현력이 있는 것은 아니지만, 나중에 확장할 것이다.
이 글의 나머지에서는 서로 다른 최적화들이 6개의 샘플 프로그램 실행 시간에 어떤 영향을 미치는지 살펴본다. brainfuck 코드는 C 코드로 컴파일되고, 그 C 코드는 gcc 4.8.2로 다시 컴파일된다. gcc 최적화 엔진의 이점을 가능한 한 덜 얻기 위해 최적화 레벨 0(-O0)을 사용한다. 실행 시간은 Ubuntu Trusty를 구동하는 Lenovo x240에서 10회 실행의 평균 실측 시간(real time)으로 측정했다.
Brainfuck 코드는 종종 +, -, <, >의 긴 연속으로 가득하다. 우리의 순진한 매핑에서는, 이 명령어 각각이 C 코드 한 줄을 만들어낸다. 예를 들어 다음(다소 인위적인) brainfuck 조각을 보자:
+++++[->>>++<<<]>>>.
이 프로그램은 아스키 개행 문자(ascii 10, ‘\n’)를 출력한다. 첫 번째 + 연속은 현재 셀에 5를 저장한다. 그 다음 루프가 있는데, 각 반복에서 현재 셀에서 1을 빼고 오른쪽으로 3칸 떨어진 다른 셀에 2를 더한다. 루프는 5번 실행되므로, 오프셋 3의 셀은 10(2×5)으로 설정된다. 마지막으로 이 셀을 출력한다.
순진한 C 매핑을 사용하면 다음 코드를 얻는다:
mem[p]++;
mem[p]++;
mem[p]++;
mem[p]++;
mem[p]++;
while (mem[p]) {
mem[p]--;
p++;
p++;
p++;
mem[p]++;
mem[p]++;
p--;
p--;
p--;
}
p++;
p++;
p++;
putchar(mem[p]);
확실히 더 나아질 여지가 있다. 다음 네 가지 IR 연산을 확장해서, 연산을 x번 적용한다는 뜻의 단일 인자 x를 받도록 하자:
| IR | C |
|---|---|
Add(x) | mem[p] += x; |
Sub(x) | mem[p] -= x; |
Right(x) | p += x; |
Left(x) | p -= x; |
Out | putchar(mem[p]); |
In | mem[p] = getchar(); |
Open | while(mem[p]) { |
Close | } |
이를 위 스니펫에 적용하면 훨씬 간결한 C 코드가 된다:
mem[p] += 5;
while (mem[p]) {
mem[p] -= 1;
p += 3;
mem[p] += 2;
p -= 3;
}
p += 3;
putchar(mem[p]);
6개 샘플 프로그램의 코드를 분석해 보면 고무적이다. 예를 들어 factor.b, hanoi.b, mandelbrot.b의 명령어 중 약 75%는 수축 가능(contractable)하다. 즉, 바로 인접한 >, +, <, -가 최소 2개 이상 연속된 구간의 일부다. 40% 정도인 것은 dbfi.b와 long.b이며, awib-0.4.b는 60%다. 다만 이런 수치만 보고 과신하면 안 된다. 이런 연속 구간이 실제로는 거의 실행되지 않을 수도 있다. 실제 속도 향상 측정을 보자.
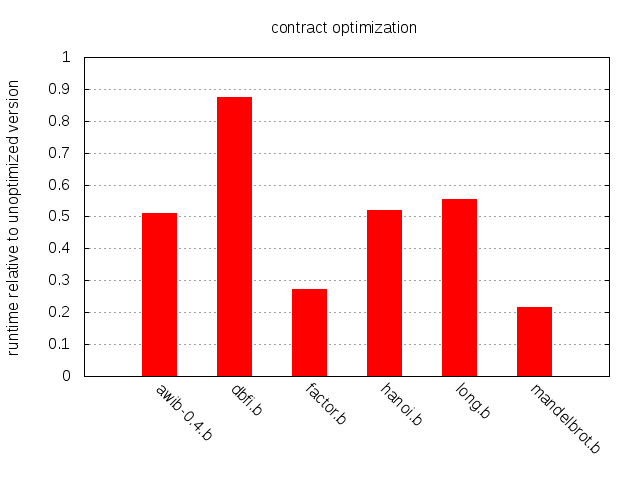
전반적으로 영향이 인상적이며, 특히 mandelbrot.b와 factor.b에서 두드러진다. 반대로 dbfi.b는 스펙트럼의 다른 끝에 있다. 결론적으로 수축은 구현이 쉽고 효과적인 최적화로 보이며, 모든 brainfuck 컴파일러가 고려할 만하다.
brainfuck의 흔한 관용구 중 하나는 클리어 루프 [-]다. 이 루프는 현재 셀에서 1을 빼고, 셀이 0이 될 때까지 반복한다. 순진하게 실행하면 클리어 루프의 실행 시간은 셀이 가질 수 있는 최대값(보통 255)에 비례할 수 있다.
더 나아질 수 있다. IR에 Clear 연산을 도입하자.
| IR | C |
|---|---|
Add | mem[p]++; |
Sub | mem[p]--; |
Right | p++; |
Left | p--; |
Out | putchar(mem[p]); |
In | mem[p] = getchar(); |
Open | while(mem[p]) { |
Close | } |
Clear | mem[p] = 0; |
[-]의 모든 발생을 Clear로 컴파일하는 것에 더해, [+]도 동일하게 처리할 수 있다. 이는 (상식적인 모든 구현의) brainfuck 메모리 모델이 최대값을 넘으면 0으로 래핑되는 셀을 제공하기 때문에 가능하다.
샘플 프로그램을 살펴보면 hanoi.b와 long.b의 명령어 중 약 8%가 클리어 루프의 일부이며, 다른 프로그램들은 약 2% 정도다.
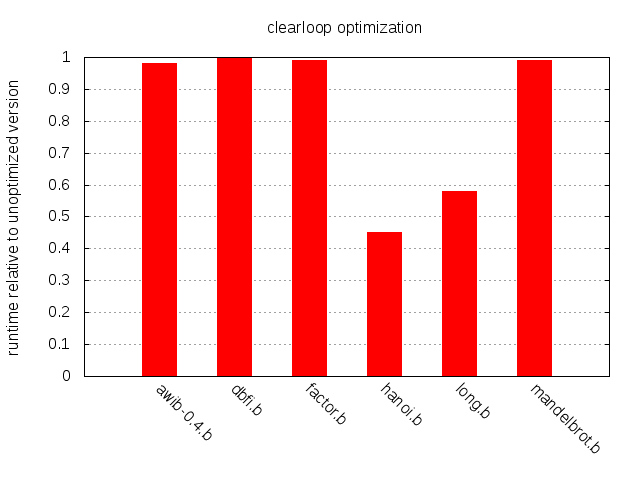
예상대로 클리어 루프 최적화의 영향은 long.b와 hanoi.b를 제외하면 모두 미미하지만, 이 둘에서의 속도 향상은 인상적이다. 결론: 클리어 루프 최적화는 구현이 단순하고, 경우에 따라 큰 영향을 준다. 추천.
또 다른 흔한 구성은 복사 루프다. 예를 들어 [->+>+<<] 같은 스니펫을 보자. 클리어 루프처럼 본문은 현재 셀에서 1을 빼고 0이 될 때까지 반복한다. 하지만 부수 효과가 있다. 각 반복에서 본문은 현재 셀보다 위(오른쪽)로 1칸, 2칸 떨어진 두 셀에 1씩 더한다. 결과적으로 현재 셀을 비우는 동시에, 원래 값이 다른 두 셀에 더해진다.
IR에 Copy(x)라는 새 연산을 도입하자. 이는 현재 셀의 복사본을 오프셋 x의 셀에 더한다.
| IR | C |
|---|---|
Add(x) | mem[p] += x; |
Sub(x) | mem[p] -= x; |
Right(x) | p += x; |
Left(x) | p -= x; |
Out | putchar(mem[p]); |
In | mem[p] = getchar(); |
Open | while(mem[p]) { |
Close | } |
Clear | mem[p] = 0; |
Copy(x) | mem[p+x] += mem[p]; |
이를 복사 루프 예시([->+>+<<])에 적용하면 Copy(1), Copy(2), Clear라는 세 개의 IR 연산이 되고, 이는 다시 다음 C 코드로 컴파일된다:
mem[p+1] += mem[p];
mem[p+2] += mem[p];
mem[p] = 0;
이는 상수 시간에 실행된다. 반면 순진한 루프 구현은 mem[p]에 들어 있는 값만큼 반복한다.
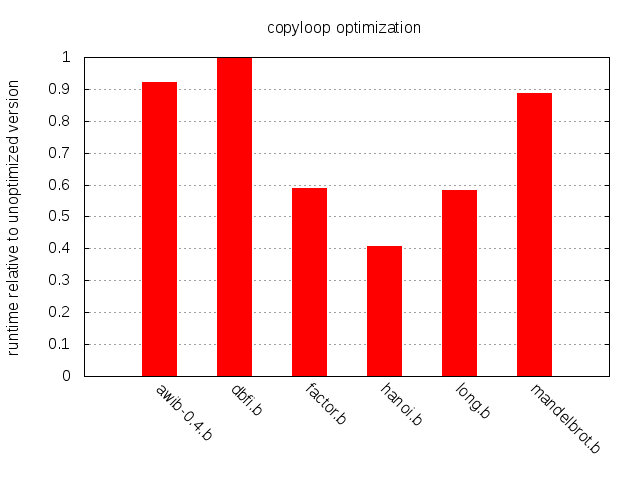
dbfi.b를 제외하면 전반적으로 개선된다.
같은 맥락에서, 복사 루프는 곱셈 루프로 일반화할 수 있다. [->+++>+++++++<<] 같은 brainfuck 코드는 일반적인 복사 루프처럼 동작하지만, 현재 셀의 복사본에 곱셈 계수를 도입한다. 이는 다음처럼 컴파일할 수 있다:
mem[p+1] += mem[p] * 3;
mem[p+2] += mem[p] * 7;
mem[p] = 0
Copy 연산을 더 일반적인 Mul 연산으로 대체하고, 샘플 프로그램에 어떤 영향을 주는지 보자.
| IR | C |
|---|---|
Add(x) | mem[p] += x; |
Sub(x) | mem[p] -= x; |
Right(x) | p += x; |
Left(x) | p -= x; |
Out | putchar(mem[p]); |
In | mem[p] = getchar(); |
Open | while(mem[p]) { |
Close | } |
Clear | mem[p] = 0; |
Mul(x, y) | mem[p+x] += mem[p] * y; |
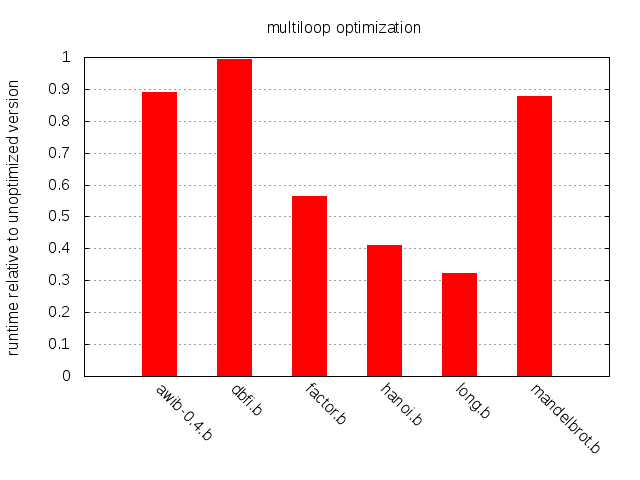
대부분의 프로그램은 Copy에서 Mul로 전환하면서 약간의 이득을 보지만, long.b는 크게 개선되고 hanoi.b는 전혀 개선되지 않는다. 설명은 간단하다. long.b에는 복사 루프가 없고 깊게 중첩된 곱셈 루프가 하나 있다. hanoi.b에는 곱셈 루프가 없지만 복사 루프는 많다.
지금까지는 대부분의 샘플 프로그램 성능을 개선할 수 있었지만, dbfi.b는 여전히 잡히지 않았다. 소스 코드를 살펴보면 흥미로운 점이 있다. dbfi.b의 429개 명령어 중 무려 8%가 [<]와 [>] 같은 루프 안에 있다. awib-0.4는 0.8%이고, 다른 프로그램들은 이 구성의 발생이 전혀 없다. 이 코드 조각들은 0인 셀을 만날 때까지(각각 왼쪽 또는 오른쪽으로) 포인터를 반복해서 이동한다. 이전 글에서 이들이 어떻게 활용될 수 있는지 좋은 예시를 봤다.
이 루프들이 0이 아닌 셀들의 연속 구간을 스캔해 지나가는 것이 흔하고 중요한 사용 사례이긴 하지만, 그것만이 전부는 아니다. 예를 들어 같은 구성은 +<[>-]>[>]< 같은 스니펫에도 나타날 수 있는데, 정확한 의미는 독자에게 연습 문제로 남겨두겠다. 그렇긴 해도, 큰 메모리 영역을 가로지르는 스캔은 매우 시간 소모적일 수 있으며, 최적화의 주된 대상으로 볼 수 있다.
다행히도, 특정 바이트의 발생을 메모리 영역에서 효율적으로 찾는 문제는 C 표준 라이브러리의 memchr() 함수로 대부분 해결되어 있다. “뒤로” 스캔하는 경우는 GNU 확장인 memrchr()로 처리된다. 요컨대 이 함수들은 전체 메모리 워드(보통 32비트 또는 64비트)를 CPU 레지스터로 로드한 뒤, 개별 8비트 구성요소들을 병렬로 검사한다. 이는 바이트를 하나씩 로드하고 검사하는 것보다 훨씬 효율적이다.
IR을 확장해 두 개의 새 연산 ScanLeft와 ScanRight를 추가하자.
| IR | C |
|---|---|
Add(x) | mem[p] += x; |
Sub(x) | mem[p] -= x; |
Right(x) | p += x; |
Left(x) | p -= x; |
Out | putchar(mem[p]); |
In | mem[p] = getchar(); |
Open | while(mem[p]) { |
Close | } |
Clear | mem[p] = 0; |
Mul(x, y) | mem[p+x] += mem[p] * y; |
ScanLeft | p -= (long)((void *)(mem + p) - memrchr(mem, 0, p + 1)); |
ScanRight | p += (long)(memchr(mem + p, 0, sizeof(mem)) - (void *)(mem + p)); |
배열 인덱스를 직접 포인터 조작 대신 사용한다는 불행한 결과로, 스캔 연산의 C 버전은 꽤 끔찍해 보인다. 뭐, 인생이 그렇다.
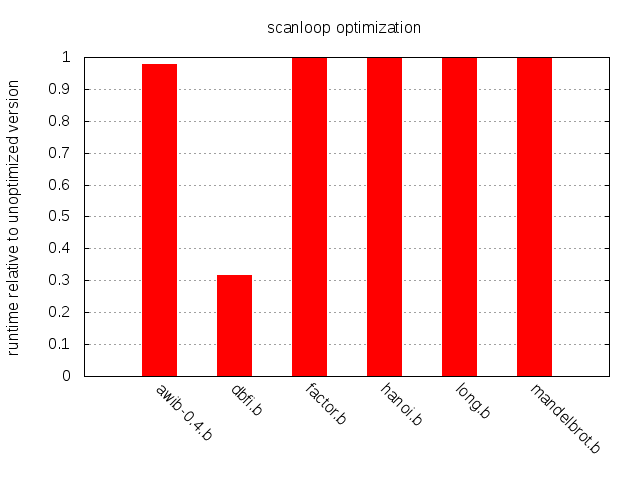
dbfi.b는 3배가 넘는 속도 향상을 얻고, 다른 프로그램들은 개선이 거의 없거나 전혀 없다. 물론 다른 libc 구현이나 다른 아키텍처에서 memchr()가 동일하게 잘 동작하리라는 보장은 없다. 하지만 효율적이고 이식 가능한 memchr() 및 memrchr() 구현들이 존재하므로, 컴파일러가 이 함수들을 번들로 포함하는 것도 어렵지 않다.
복사 루프 최적화와 곱셈 루프 최적화는 흥미로운 공통점이 있다. 둘 다 현재 셀로부터 오프셋이 있는 위치에서 산술 연산을 수행한다. brainfuck에서는 루프가 아닌 연산들이 길게 이어진 시퀀스를 자주 보게 되며, 이 시퀀스에는 보통 <와 >가 꽤 많이 포함된다. 포인터를 이리저리 움직이는 데 시간을 낭비할 이유가 있을까? 루프가 아닌 명령어들에 대해 오프셋을 미리 계산하고, 시퀀스 끝에서만 포인터를 갱신하면 어떨까?
| IR | C |
|---|---|
Add(x, off) | mem[p+off] += x; |
Sub(x, off) | mem[p+off] -= x; |
Right(x) | p += x; |
Left(x) | p -= x; |
Out(off) | putchar(mem[p+off]); |
In(off) | mem[p+off] = getchar(); |
Clear(off) | mem[p+off] = 0; |
Mul(x, y, off) | mem[p+x+off] += mem[p+off] * y; |
ScanLeft | p -= (long)((void *)(mem + p) - memrchr(mem, 0, p + 1)); |
ScanRight | p += (long)(memchr(mem + p, 0, sizeof(mem)) - (void *)(mem + p)); |
Clear와 Mul이 이 표에 포함되어 있긴 하지만, 테스트는 연산 오프셋 최적화만 단독으로 적용한 상태에서 수행되었기 때문에 컴파일러는 이 두 연산을 결코 생성하지 않았다.
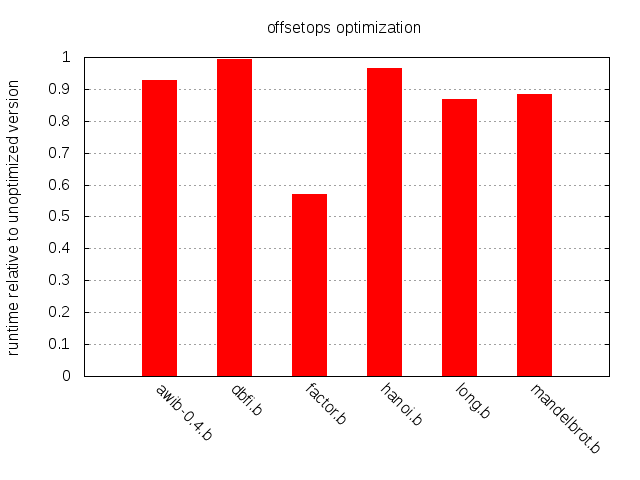
체감 가능한 결과이긴 하지만 다소 미미하다.
마무리로, 이 모든 최적화를 샘플 프로그램들에 적용했을 때 무엇을 달성할 수 있는지 보자.
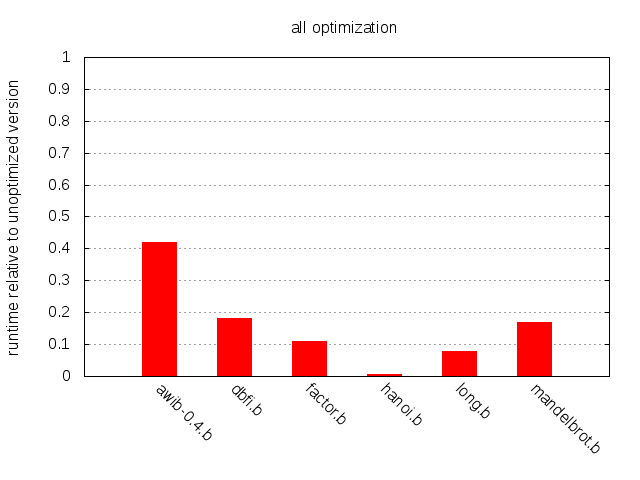
전반적으로 큰 개선이 있으며, hanoi.b의 경우 약 130배에서 awib-0.4의 2.4배 향상까지 다양하다.
비교적 단순한 기법들이 샘플 프로그램들의 성능을 크게 개선할 수 있음을 확인했다. brainfuck 컴파일러 작성자라면 최소한 그중 일부는 구현하는 것을 고려해야 한다. 물론 brainfuck 같은 난해한 언어에 시간과 노력을 쓰는 것은 무의미한 연습처럼 보일 수도 있다. 하지만 여기의 개념들 중 일부는 더 현실적인 환경에도 적용될 수 있다고 우리는 희망하고 또한 믿는다. 그리고 brainfuck를 가지고 이것저것 해보는 건 그냥 재미있다.
이상이다.
See also: hacker news에서의 토론
Copyleft © 2014-2016 Mats Linander, all rights reversed