삼각함수(코사인)만으로 Fizz Buzz 규칙을 하나의 닫힌식으로 표현하고, 지시함수와 복소지수, 이산 푸리에 변환을 통해 그 공식을 도출한다.
제목: 코사인으로 푸는 Fizz Buzz
글: Susam Pal (2025년 11월 20일)
Fizz Buzz는 기초 프로그래밍 실력을 간단히 시험해 보기 위해 프로그래머 세계에서 이상할 정도로 인기를 끈 숫자 세기 게임이다. 규칙은 간단하다. 1부터 시작하여 숫자를 순서대로 큰 소리로 말한다. 어떤 수가 3으로 나누어떨어지면 숫자 대신 'Fizz'라고 말한다. 5로 나누어떨어지면 'Buzz'라고 말한다. 3과 5로 모두 나누어떨어지면 'Fizz'와 'Buzz'를 함께 말한다. 다음은 이 수열을 출력하는 전형적인 Python 프로그램이다:
for n in range(1, 101):
if n % 15 == 0:
print('FizzBuzz')
elif n % 3 == 0:
print('Fizz')
elif n % 5 == 0:
print('Buzz')
else:
print(n)
출력은 여기서 볼 수 있다: fizz-buzz.txt. 이 프로그램을 더 복잡하게 만들 수 있을까? 'Fizz', 'Buzz', 'FizzBuzz'는 수열 전체에 걸쳐 주기적으로 반복된다. 또 무엇이 주기적인가? 삼각함수다! 어쩌면 삼각함수를 이용해 이 수열의 네 가지 규칙을 하나의 닫힌식으로 담아낼 수 있을지도 모른다. 이 글에서는 바로 그 아이디어를 탐구한다. 끝까지 가면 임의의 정수 n을 넣으면 출력할 텍스트를 선택해 주는 이산 푸리에 급수를 얻게 될 것이다.
더 나아가기 전에 Fizz Buzz 수열에 대한 엄밀한 수학적 정의를 세우자. 먼저 나중에 Fizz Buzz 수열을 정의하는 데 도움이 될 몇 가지 함수를 도입한다.
정수 n에 대해 네 개의 함수 집합 {s_0, s_1, s_2, s_3}를 다음과 같이 정의한다:
\begin{align*} s_0(n) &= n, \ s_1(n) &= \mathtt{Fizz}, \ s_2(n) &= \mathtt{Buzz}, \ s_3(n) &= \mathtt{FizzBuzz}. \end{align*}
이들을 기호 함수라고 부르는데, Fizz Buzz 수열에 나타나는 모든 항을 생성하기 때문이다. 기호 함수 s_0는 n 자체를 반환한다. 함수 s_1, s_2, s_3는 상수 함수로서 n의 값과 무관하게 각각 리터럴 단어 \mathtt{Fizz}, \mathtt{Buzz}, \mathtt{FizzBuzz}를 항상 반환한다.
이제 Fizz Buzz 수열을 (s_{f(n)}(n))_{n = 1}^{\infty}로 정의하자. 여기서
[ f(n) = \begin{cases} 1 & \text{if } 3 \mid n \text{ and } 5 \nmid n, \ 2 & \text{if } 3 \nmid n \text{ and } 5 \mid n, \ 3 & \text{if } 3 \mid n \text{ and } 5 \mid n, \ 0 & \text{otherwise}. \end{cases} ]
여기서 표기 m \mid n은 정수 m이 정수 n을 나눈다는 뜻, 즉 n이 m의 배수임을 의미한다. 동치로, 어떤 정수 c가 존재하여 n = c m가 된다. 이에 반해 m \nmid n은 m이 n을 나누지 못한다는 뜻, 즉 n이 m의 배수가 아님을 의미한다.
위 정의로 수열의 처음 몇 항을 전개하면 다음과 같다:
\begin{align*} (s_{f(n)}(n)){n = 1}^{\infty} &= (s{f(1)}(1),; s_{f(2)}(2),; s_{f(3)}(3),; s_{f(4)}(4),; s_{f(5)}(5),; s_{f(6)}(6),; s_{f(7)}(7),; \dots) \ &= (s_0(1),; s_0(2),; s_1(3),; s_0(4),; s_2(5),; s_1(6),; s_0(7),; \dots) \ &= (1,; 2,; \mathtt{Fizz},; 4,; \mathtt{Buzz},; \mathtt{Fizz},; 7,; \dots). \end{align*}
함수 f(n)이 인덱스 i를 만들어 내고, 그 i로 기호 함수 s_i(n)을 선택하여 n번째 항을 생성한다는 점에 주목하라. 따라서 f(n)을 인덱스 함수라고 부른다.
앞 절의 인덱스 함수 f(n)을 경우와 조건의 순서를 바꾸어 흥미로운 패턴을 더 잘 보이게 적어 보자:
[ f(n) = \begin{cases} 0 & \text{if } 5 \nmid n \text{ and } 3 \nmid n, \ 1 & \text{if } 5 \nmid n \text{ and } 3 \mid n, \ 2 & \text{if } 5 \mid n \text{ and } 3 \nmid n, \ 3 & \text{if } 5 \mid n \text{ and } 3 \mid n. \end{cases} ]
이 함수는 다시 다른 함수 s_{f(n)}(n)을 선택하게 해 주고, 그 결과 Fizz Buzz 수열의 n번째 항이 결정된다. 이제 목표는 이 조각별 정의를 하나의 닫힌식으로 바꾸는 것이다. 이를 위해 먼저 지시 함수 I_m(n)을 다음과 같이 정의한다:
[ I_m(n) = \begin{cases} 1 & \text{if } m \mid n, \ 0 & \text{if } m \nmid n. \end{cases} ]
이제 f(n)의 공식을 다음과 같이 쓸 수 있다:
[ f(n) = \begin{cases} 0 & \text{if } I_5(n) = 0 \text{ and } I_3(n) = 0, \ 1 & \text{if } I_5(n) = 0 \text{ and } I_3(n) = 1, \ 2 & \text{if } I_5(n) = 1 \text{ and } I_3(n) = 0, \ 3 & \text{if } I_5(n) = 1 \text{ and } I_3(n) = 1. \end{cases} ]
패턴이 보이는가? 같은 내용을 표로 쓰면 다음과 같다:
| I_5(n) | I_3(n) | f(n) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 2 |
| 1 | 1 | 3 |
이제 보이는가? 첫 두 열의 값을 이진수의 각 자리로, 세 번째 열의 값을 10진수로 보면 각 행에서 첫 두 열이 세 번째 열의 이진 표현이 된다. 예를 들어 3_{10} = 11_2이고, 실제로 표의 마지막 행에서 두 비트가 1과 1이며 마지막 열의 수는 3이다. 다시 말해 I_5(n)과 I_3(n)의 값을 옆으로 나란히 쓰면 f(n)의 이진 표현이 된다. 따라서
[ f(n) = 2, I_5(n) + I_3(n). ]
다음의 작은 프로그램으로 이 공식을 확인할 수 있다:
for n in range(1, 101):
s = [n, 'Fizz', 'Buzz', 'FizzBuzz']
i = (n % 3 == 0) + 2 * (n % 5 == 0)
print(s[i])
조금 덜 명확해지지만 더 짧게도 쓸 수 있다:
for n in range(1, 101):
print([n, 'Fizz', 'Buzz', 'FizzBuzz'][(n % 3 == 0) + 2 * (n % 5 == 0)])
지금까지 얻은 것도 꽤 괜찮다. 닫힌식(closed-form)의 보편적인 정의가 있는 것은 아니지만, 위에서 정의한 지시 함수는 닫힌식에서 허용될 만큼 충분히 단순하다고 대부분 동의할 것이다.
앞 절에서 얻은 공식은 f(n) = I_3(n) + 2, I_5(n)이며, 이를 인덱스로 사용해 출력할 텍스트를 찾아냈다. 이 자체로도 이미 꽤 괜찮은 닫힌식이라고 주장했다.
하지만 더 복잡하게 만들겠다는 취지에서, 이런 의문을 던져 보자. 지시 함수를 사용할 수 없다면? 덧셈, 뺄셈, 곱셈, 나눗셈, 정수 지수와 정수 인덱스의 근, 그리고 지수·로그·삼각함수 같은 통상 허용되는 기본 연산과 함수만으로 닫힌식을 써야 한다면? 놀랍게도 위 공식은 덧셈, 곱셈, 나눗셈, 그리고 코사인만으로 다시 쓸 수 있다. 이제 변환을 시작하자.
다음의 합을 생각하자:
[ S_m(n) = \sum_{k = 0}^{m - 1} e^{2 \pi i k n / m}, ]
여기서 i는 허수 단위이고 n, m은 정수다. 이것은 공비가 r = e^{2\pi i n/m}인 복소평면에서의 등비수열이다. 만약 n이 m의 배수라면 n = c m인 정수 c가 존재하고, 따라서 r = e^{2\pi i n/m} = e^{2\pi i c} = 1이 된다. 그러므로 n이 m의 배수일 때
[ S_m(n) = \sum_{k = 0}^{m - 1} e^{2 \pi i k n / m} = \sum_{k = 0}^{m - 1} 1^k = m. ]
n이 m의 배수가 아니라면 r \ne 1이므로 등비수열의 합은
[ S_m(n) = \frac{r^m - 1}{r - 1} = \frac{e^{2 \pi i n} - 1}{e^{2 \pi i n / m} - 1} = 0. ]
따라서
[ S_m(n) = \begin{cases} m & \text{if } m \mid n, \ 0 & \text{if } m \nmid n. \end{cases} ]
양변을 m으로 나누면
[ \frac{S_m(n)}{m} = \begin{cases} 1 & \text{if } m \mid n, \ 0 & \text{if } m \nmid n. \end{cases} ]
오른쪽은 바로 I_m(n)이므로
[ I_m(n) = \frac{S_m(n)}{m} = \frac{1}{m} \sum_{k = 0}^{m - 1} e^{2 \pi i k n / m}. ]
오일러 공식 e^{i x} = \cos x + i \sin x(실수 x에 대해)에서 시작하자. 이로부터 e^{i x} + e^{-i x} = 2 \cos x를 얻는다. 따라서
\begin{align*} I_3(n) &= \frac{1}{3} \sum_{k = 0}^2 e^{2 \pi i k n / 3} \ &= \frac{1}{3} \left( 1 + e^{2 \pi i n / 3} + e^{4 \pi i n / 3} \right) \ &= \frac{1}{3} \left( 1 + e^{2 \pi i n / 3} + e^{-2 \pi i n / 3} \right) \ &= \frac{1}{3} + \frac{2}{3} \cos \left( \frac{2 \pi n}{3} \right). \end{align*}
위의 세 번째 등식은 e^{4 \pi i n / 3} = e^{6 \pi i n / 3} e^{-2 \pi i n / 3} = e^{2 \pi i n} e^{-2 \pi i n/3} = e^{-2 \pi i n / 3}에서 따른다.
위 함수는 n의 정수값에 대해 정의되지만, 공식을 실수 x로 확장해 그래프를 그리면 정수 사이의 모양도 볼 수 있다. 예상대로, x가 3의 정수배일 때 값이 1이 되고, 3으로 나누어떨어지지 않는 정수일 때 값이 0이 된다.
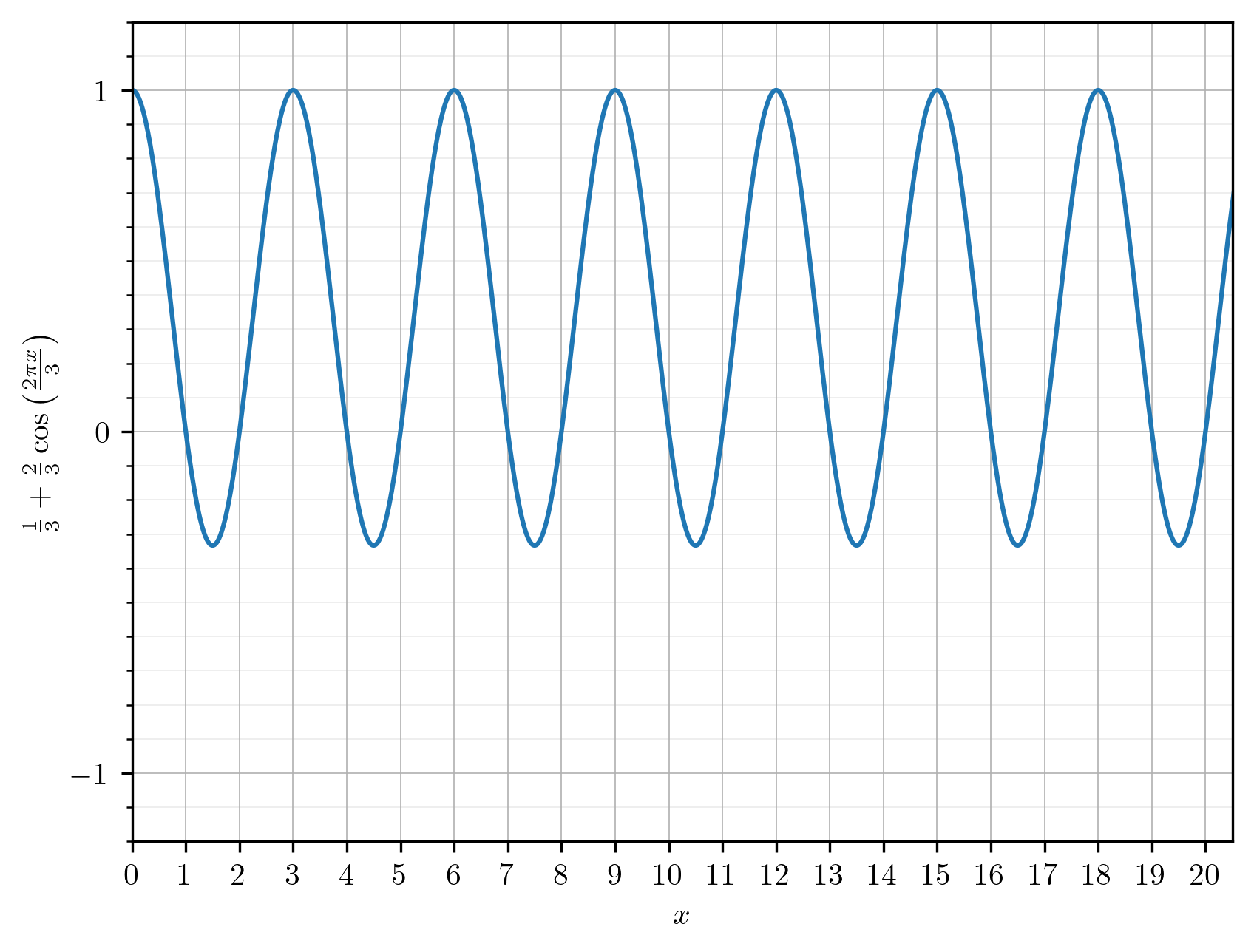
1/3 + (2/3) cos(2\pi x/3)의 그래프
마찬가지로
\begin{align*} I_5(n) &= \frac{1}{5} \sum_{k = 0}^4 e^{2 \pi i k n / 5} \ &= \frac{1}{5} \left( 1 + e^{2 \pi i n / 5} + e^{4 \pi i n / 5} + e^{6 \pi i n / 5} + e^{8 \pi i n / 5} \right) \ &= \frac{1}{5} \left( 1 + e^{2 \pi i n / 5} + e^{4 \pi i n / 5} + e^{-4 \pi i n / 5} + e^{-2 \pi i n / 5} \right) \ &= \frac{1}{5} + \frac{2}{5} \cos \left( \frac{2 \pi n}{5} \right) + \frac{2}{5} \cos \left( \frac{4 \pi n}{5} \right). \end{align*}
이 표현도 실수 x로 확장하여 그래프를 그릴 수 있다. 역시 함수 값은 5의 정수배에서 1이 되고, 5로 나누어떨어지지 않는 정수에서 0이 된다.
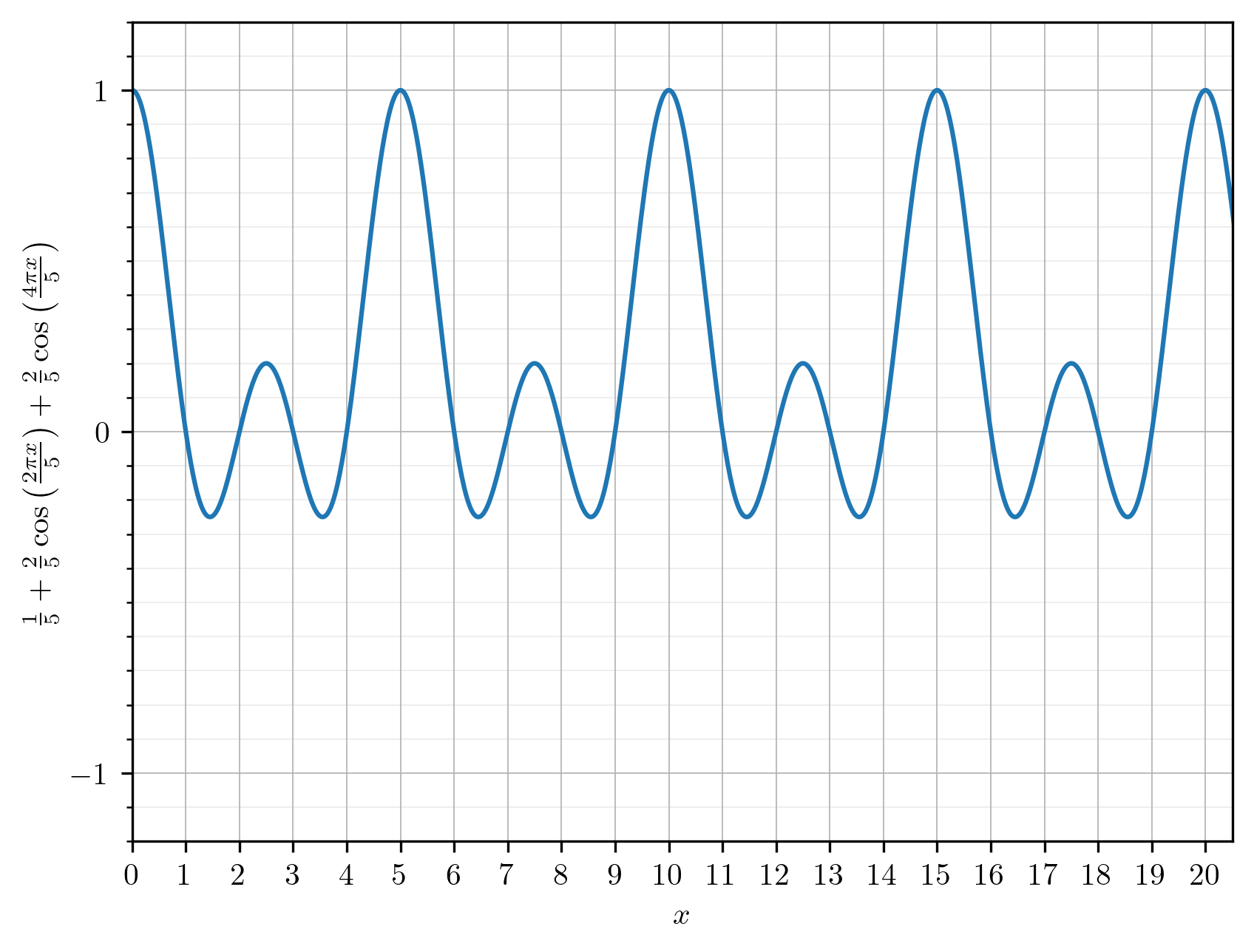
1/5 + (2/5) cos(2\pi x/5) + (2/5) cos(4\pi x/5)의 그래프
앞서 f(n)을 f(n) = I_3(n) + 2, I_5(n)으로 썼음을 기억하자. 여기에 위의 삼각함수 표현을 대입하면
[ f(n) = \frac{1}{3} + \frac{2}{3} \cos \left( \frac{2 \pi n}{3} \right) + 2 \cdot \left( \frac{1}{5} + \frac{2}{5} \cos \left( \frac{2 \pi n}{5} \right) + \frac{2}{5} \cos \left( \frac{4 \pi n}{5} \right) \right). ]
간단히 정리하면
[ f(n) = \frac{11}{15} + \frac{2}{3} \cos \left( \frac{2 \pi n}{3} \right) + \frac{4}{5} \cos \left( \frac{2 \pi n}{5} \right) + \frac{4}{5} \cos \left( \frac{4 \pi n}{5} \right). ]
이 표현 역시 실수 x로 확장해 그려 볼 수 있다. 그 결과 곡선은 정수점에서 0, 1, 2, 3의 값을 원하는 대로 취한다.
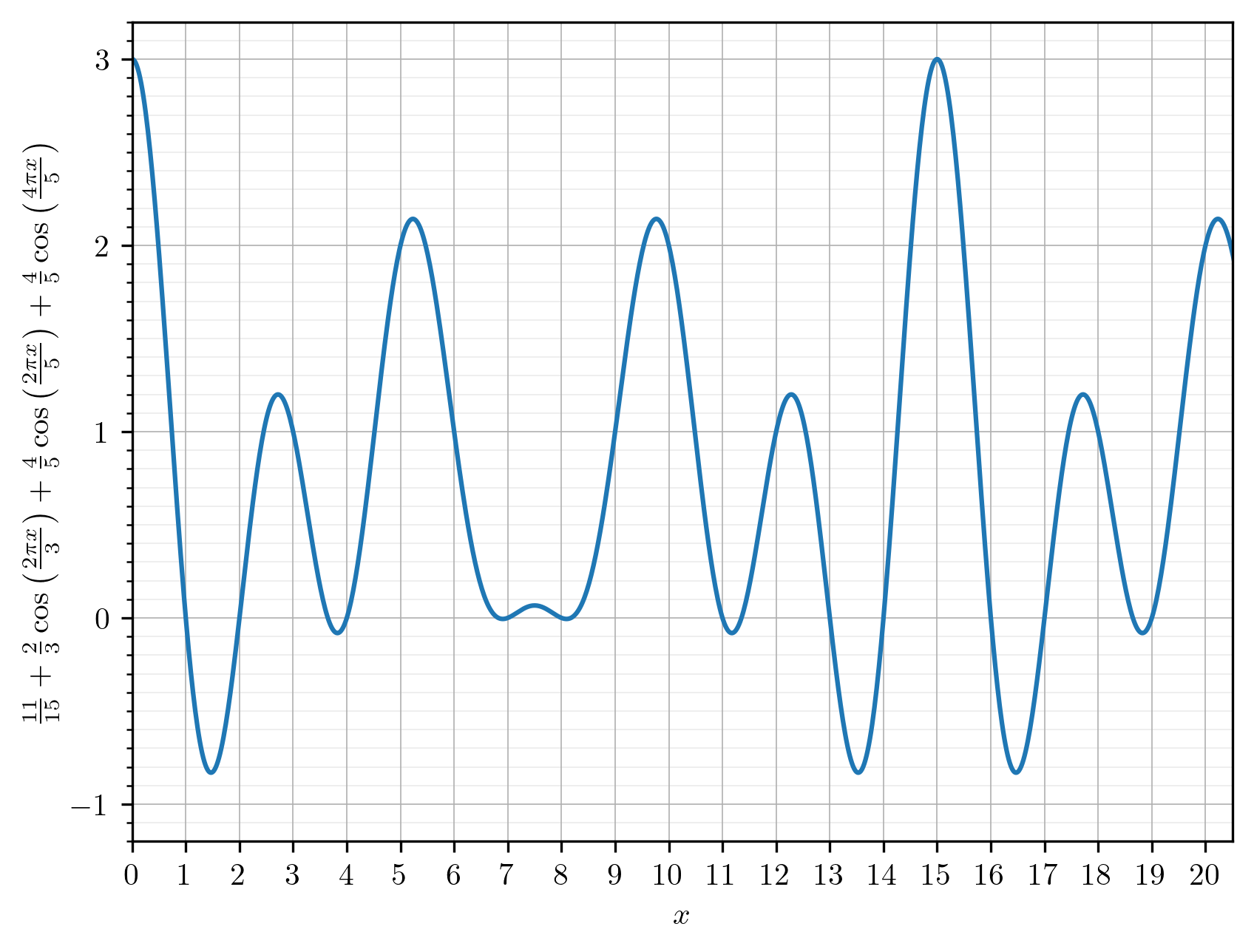
11/15 + (2/3) cos(2\pi x/3) + (4/5) cos(2\pi x/5) + (4/5) cos(4\pi x/5)의 그래프
이제 Python 프로그램을 다음과 같이 쓸 수 있다:
from math import cos, pi
for n in range(1, 101):
s = [n, 'Fizz', 'Buzz', 'FizzBuzz']
i = round(11 / 15 + (2 / 3) * cos(2 * pi * n / 3)
+ (4 / 5) * cos(2 * pi * n / 5)
+ (4 / 5) * cos(4 * pi * n / 5))
print(s[i])
눈썰미 있는 독자는 우리가 얻은 f(n)의 표현이 유한한 푸리에 급수임을 눈치챘을 것이다. 놀랄 일은 아니다. Fizz Buzz 프로그램의 출력은 n mod 15에만 의존한다. 유한 순환군 위의 임의의 함수는 정확히 유한한 푸리에 전개로 쓸 수 있다. 이 절에서는 이산 푸리에 변환을 사용해 같은 함수 f(n)을 다시 구해 보자. 여기서 보일 계산은 손으로 하기에는 꽤 번거롭다는 점을 밝혀 둔다. 그럼에도 이러한 계수를 어떻게 구하는지 엿볼 수 있다. 끝까지 가면 앞서와 정확히 같은 f(n)에 도달하게 된다. 새로울 것은 없다. 다만 더 직접적이고 눈에 띄게 수고로운 방식으로 같은 결과를 얻을 뿐이다. 이런 이야기가 흥미롭지 않다면 이 절은 건너뛰어도 된다.
f(n)은 주기가 15인 주기 함수임을 알고 있다. 이산 푸리에 변환을 적용하기 위해 n = 1, 2, …, 15라는 하나의 완전한 주기를 살펴보자. 이 구간에서 값은 다음과 같다:
[ \begin{array}{c|ccccccccccccccc} n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 \ \hline f(n) & 0 & 0 & 1 & 0 & 2 & 1 & 0 & 0 & 1 & 2 & 0 & 1 & 0 & 0 & 3 \end{array} ]
이산 푸리에 변환은 다음과 같이 정의되는 상수들을 준다:
[ c_k = \frac{1}{15} \sum_{n = 1}^{15} f(n) e^{-2 \pi i k n / 15}, \quad k = 1, 2, \dots, 15. ]
이 상수들로 역변환을 통해 f(n)을 복원한다:
[ f(n) = \sum_{k = 1}^{15} c_k e^{2 \pi i k n / 15}, \quad n \in \mathbb{Z}. ]
첫 번째 상수를 계산해 보자:
[ c_1 = \frac{1}{15}\Big( e^{-2 \pi i\cdot 3/15} + 2 e^{-2 \pi i\cdot 5/15} + e^{-2 \pi i\cdot 6/15} + e^{-2 \pi i\cdot 9/15} + 2 e^{-2 \pi i\cdot 10/15} + e^{-2 \pi i\cdot 12/15} + 3 e^{-2 \pi i\cdot 15/15} \Big) = 0. ]
마찬가지로
[ c_2 = \frac{1}{15}\Big( e^{-2 \pi i\cdot 6/15} + 2 e^{-2 \pi i\cdot 10/15} + e^{-2 \pi i\cdot 12/15} + e^{-2 \pi i\cdot 18/15} + 2 e^{-2 \pi i\cdot 20/15} + e^{-2 \pi i\cdot 24/15} + 3 e^{-2 \pi i\cdot 30/15} \Big) = 0. ]
그리고
[ c_3 = \frac{1}{15}\Big( e^{-2 \pi i\cdot 9/15} + 2 e^{-2 \pi i\cdot 15/15} + e^{-2 \pi i\cdot 18/15} + e^{-2 \pi i\cdot 27/15} + 2 e^{-2 \pi i\cdot 30/15} + e^{-2 \pi i\cdot 36/15} + 3 e^{-2 \pi i\cdot 45/15} \Big) = \frac{2}{5}. ]
이와 같은 방식으로 모든 상수를 구하면 다음과 같다:
\begin{align*} c_1 &= c_2 = c_4 = c_7 = c_8 = c_{11} = c_{13} = c_{14} = 0, \ c_3 &= c_6 = c_9 = c_{12} = \frac{2}{5}, \ c_5 &= c_{10} = \frac{1}{3}, \ c_{15} &= \frac{11}{15}. \end{align*}
역변환을 사용하면
\begin{align*} f(n) &= \sum_{k = 1}^{15} c_k , e^{2 \pi i k n / 15} \ &= \frac{11}{15} + \frac{2}{5} \left( e^{2 \pi i\cdot 3n/15} + e^{2 \pi i\cdot 6n/15} + e^{2 \pi i\cdot 9n/15} + e^{2 \pi i\cdot 12n/15} \right) \ &\phantom{=} + \frac{1}{3} \left( e^{2 \pi i\cdot 5n/15} + e^{2 \pi i\cdot 10n/15} \right) \ &= \frac{11}{15} + \frac{2}{5} \left( e^{6 \pi i n/15} + e^{12 \pi i n/15} + e^{18 \pi i n/15} + e^{24 \pi i n/15} \right) \ &\phantom{=} + \frac{1}{3} \left( e^{10 \pi i n/15} + e^{20 \pi i n/15} \right) \ &= \frac{11}{15} + \frac{2}{5} \left( e^{6 \pi i n/15} + e^{12 \pi i n/15} + e^{-12 \pi i n/15} + e^{-6 \pi i n/15} \right) \ &\phantom{=} + \frac{1}{3} \left( e^{10 \pi i n/15} + e^{-10 \pi i n/15} \right) \ &= \frac{11}{15} + \frac{2}{5} \left( 2 \cos \left( \frac{6 \pi n}{15} \right) + 2 \cos \left( \frac{12 \pi n}{15} \right) \right) \ &\phantom{=} + \frac{1}{3} \left( 2 \cos \left( \frac{10 \pi n}{15} \right) \right) \ &= \frac{11}{15} + \frac{4}{5} \cos \left( \frac{2 \pi n}{5} \right) + \frac{4}{5} \cos \left( \frac{4 \pi n}{5} \right) + \frac{2}{3} \cos \left( \frac{2 \pi n}{3} \right). \end{align*}
이는 앞서 얻은 것과 정확히 같은 f(n)이다. 달라진 점은 도달 방식뿐이다. 푸리에 계수를 손으로 구하는 일은 느리고 기계적이다. 실제로는 이런 합을 거의 항상 수치 소프트웨어나 컴퓨터 대수 시스템이 자동으로 계산한다. 그럼에도 이 연습은 우리의 소박한 Fizz Buzz 인덱스 함수가 푸리에 해석의 장치를 사용해 정확히 표현될 수 있음을 보여 준다.
요약하면, 우리는 Fizz Buzz 수열을 (s_{f(n)}(n))_{n = 1}^{\infty}로 정의했고, 여기서
[ f(n) = \frac{11}{15} + \frac{2}{3} \cos \left( \frac{2 \pi n}{3} \right) + \frac{4}{5} \cos \left( \frac{2 \pi n}{5} \right) + \frac{4}{5} \cos \left( \frac{4 \pi n}{5} \right) ]
이며, s_0(n) = n, s_1(n) = \mathtt{Fizz}, s_2(n) = \mathtt{Buzz}, s_3(n) = \mathtt{FizzBuzz}이다. 이 정의에 기반하여 Fizz Buzz 수열을 출력하는 Python 프로그램을 앞에서 보였다. 그 프로그램은 다음처럼 더 간결하게도 쓸 수 있다:
from math import cos, pi
for n in range(1, 101):
print([n, 'Fizz', 'Buzz', 'FizzBuzz'][round(11 / 15 + (2 / 3) * cos(2 * pi * n / 3) + (4 / 5) * (cos(2 * pi * n / 5) + cos(4 * pi * n / 5)))])
친구나 가족에게 공유해 깜짝 놀라게 하고 싶다면, 셸 원라이너로 이렇게 감쌀 수도 있다:
python3 -c 'from math import cos, pi; [print([n, "Fizz", "Buzz", "FizzBuzz"][round(11/15 + (2/3) * cos(2*pi*n/3) + (4/5) * (cos(2*pi*n/5) + cos(4*pi*n/5)))]) for n in range(1, 101)]'
우리는 단순한 숫자 세기 게임을 삼각함수 구성물로 바꾸었다. 즉, 상수항 11/15와 계수 2/3, 4/5, 4/5를 갖는 세 개의 코사인 항으로 이루어진 유한 푸리에 급수다. 물론 이로 인해 Fizz Buzz가 쉬워지지는 않지만, 이제 모든 \mathtt{Fizz}와 \mathtt{Buzz}가 특정한 푸리에 계수 집합 덕분에 존재하게 되었음을 보여 준다. 단순한 문제를 더 복잡하게 만들겠다는 소박한 목표로 시작했는데, 그 목표에 모자라지는 않았다고 말해도 되지 않을까.