OpenAI Triton을 MLIR 인프라로 마이그레이션/리팩터링한 초기 버전의 아키텍처와 IR, Optimizer/Backend 패스, 데이터 레이아웃, 파이프라이닝/프리패치 최적화, LLVM/PTX 인라인 어셈블리 기반 코드 생성 과정을 사례와 함께 정리한다.
2022년 11월 15일 tritonsystemtech 목차
몇 달에 걸친 끊임없는 노력 끝에, OpenAI Triton은 MLIR Infra를 향한 마이그레이션/리팩터링 작업을 성공적으로 마무리하고 최신 MLIR 기반 코드를 메인 브랜치에 머지했다. 이 작업은 최근 몇 달간 OpenAI와 NVIDIA 관련 팀이 긴밀히 협업해 완성했으며, 나 또한 운 좋게 참여할 수 있었다. 이 글에서는 일부 기술적 요약을 공유하고, 얻은 점과 생각을 기록해 보려 한다.
비록 Triton의 오픈소스 개발 속도는 현재 매우 빠르지만, 본문에서는 MLIR Infra로 리팩터링한 첫 버전의 코드만을 주로 다룬다(아마 두세 달 전의 버전이기도 하다).
OpenAI Triton paper에서는 “An Intermediate Language and Compiler for Tiled Neural Network Computations”라고 소개한다. 몇 가지 키워드가 특징을 잘 드러낸다.
Triton의 개발이 매우 빠르기 때문에, 여기서는 현재 시점의 Triton 기능만 논한다.
간단히 말해 Triton은 GPU 커널 개발을 위한 Python 기반의 언어(Language)와 고성능 컴파일러를 제공한다.
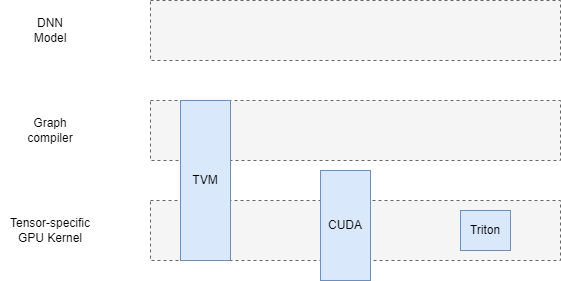 따라서 레이어 관점에서 보면, Triton의 DNN 개발 능력은 CUDA의 일부와 대응되지만 TVM, XLA와 같은 딥러닝(DL) 도메인 컴파일러와는 완전히 일대일 대응되지는 않는다. 후자는 그래프 구성부터 자동 fusion까지 엔드투엔드 능력을 갖춘 무기고에 가깝고, Triton은 보다 하위이면서도 가장 범용적인 커널 개발 문제를 겨냥한 작고 실용적인 스위스군용 칼에 더 가깝다.
따라서 레이어 관점에서 보면, Triton의 DNN 개발 능력은 CUDA의 일부와 대응되지만 TVM, XLA와 같은 딥러닝(DL) 도메인 컴파일러와는 완전히 일대일 대응되지는 않는다. 후자는 그래프 구성부터 자동 fusion까지 엔드투엔드 능력을 갖춘 무기고에 가깝고, Triton은 보다 하위이면서도 가장 범용적인 커널 개발 문제를 겨냥한 작고 실용적인 스위스군용 칼에 더 가깝다.
Triton의 새 코드 아키텍처는 대략 다음과 같이 나타낼 수 있다.
 즉, 전체적으로 세 부분으로 나눌 수 있다.
즉, 전체적으로 세 부분으로 나눌 수 있다.
이 세 부분을 관통하는 핵심 표현은 Triton의 IR이며, 미시적으로는 IR도 두 계층으로 나뉜다.
이 둘은 모두 MLIR 기반의 커스텀 dialect이다. 이 외에도 Triton은 거시적 표현을 위해 커뮤니티의 여러 dialect를 재사용한다.
std dialect: tensor, int, float 등 데이터 타입arith dialect: 각종 수학 연산scf dialect: if, for 등의 제어 흐름nvvm dialect: thread_id 등을 얻는 소수의 연산gpu dialect: printf 등 소수의 연산아래 그림은 Triton의 핵심 표현이 변환되는 전체 과정이다.
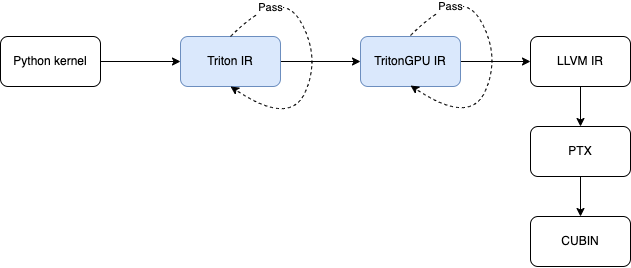 파란색 부분 두 곳이 주로 MLIR 체계와 관련된 부분이며, 이후 MLIR은 LLVM IR로 변환된다. 그 다음 Triton은 NVPTX를 호출해 PTX 어셈블리로 변환하고, 마지막으로 CUDA의 ptxas 컴파일러가 cubin을 만든다.
파란색 부분 두 곳이 주로 MLIR 체계와 관련된 부분이며, 이후 MLIR은 LLVM IR로 변환된다. 그 다음 Triton은 NVPTX를 호출해 PTX 어셈블리로 변환하고, 마지막으로 CUDA의 ptxas 컴파일러가 cubin을 만든다.
Frontend는 사용자가 Python으로 작성한 커널을 해당하는 Triton IR(Triton Dialect)로 변환한다. 지면상 자세한 내용은 생략하고, Python ast 기반 규칙은 compiler.py::CodeGenerator를 참고하면 된다.
예를 들어 vector add의 경우:
@triton.jit
def add_kernel(x_ptr, y_ptr, output_ptr, N,
BLOCK_SIZE: tl.constexpr):
pid = tl.program_id(0)
block_start = pid * BLOCK_SIZE
offsets = block_start + tl.arange(0, BLOCK_SIZE)
mask = offsets < N
x = tl.load(x_ptr + offsets, mask=mask)
y = tl.load(y_ptr + offsets, mask=mask)
output = x + y
tl.store(output_ptr+offsets, output, mask=mask)
# x, y are torch.Tensor
grid = lambda meta: (triton.cdiv(n_elements, meta['BLOCK_SIZE']),)
add_kernel[grid](x, y, output, n_elements, BLOCK_SIZE=1024)
이에 대응하는 Triton IR은 다음과 같다.
func public @kernel_0d1d2d3d(
%arg0: !tt.ptr<f32> {tt.divisibility = 16 : i32},
%arg1: !tt.ptr<f32> {tt.divisibility = 16 : i32},
%arg2: !tt.ptr<f32> {tt.divisibility = 16 : i32},
%arg3: i32 {tt.divisibility = 16 : i32}) {
%c256_i32 = arith.constant 256 : i32
%0 = tt.get_program_id {axis = 0 : i32} : i32
%1 = arith.muli %0, %c256_i32 : i32
%2 = tt.make_range {end = 256 : i32, start = 0 : i32} : tensor<256xi32>
%3 = tt.splat %1 : (i32) -> tensor<256xi32>
%4 = arith.addi %3, %2 : tensor<256xi32>
%5 = tt.splat %arg0 : (!tt.ptr<f32>) -> tensor<256x!tt.ptr<f32>>
%6 = tt.addptr %5, %4 : tensor<256x!tt.ptr<f32>>
%7 = tt.splat %arg1 : (!tt.ptr<f32>) -> tensor<256x!tt.ptr<f32>>
%8 = tt.addptr %7, %4 : tensor<256x!tt.ptr<f32>>
%9 = tt.splat %arg3 : (i32) -> tensor<256xi32>
%10 = arith.cmpi slt, %4, %9 : tensor<256xi32>
%11 = tt.load %6, %10
%12 = tt.load %8, %10
%13 = arith.addf %11, %12 : tensor<256xf32>
%14 = tt.splat %arg2 : (!tt.ptr<f32>) -> tensor<256x!tt.ptr<f32>>
%15 = tt.addptr %14, %4 : tensor<256x!tt.ptr<f32>>
tt.store %15, %13, %10 : tensor<256xf32>
return
}
보듯이 Triton IR은 원래 Python 코드와 거의 일대일로 대응되어 사용자가 정의한 computation을 MLIR 체계로 끌어들인다. 이후 이를 기반으로 다양한 최적화(Optimizer)와 더 낮은 표현으로의 변환(Backend)이 진행된다.
Optimizer는 Frontend에서 전달된 IR을 분석·최적화하여 다양한 Transformation/Conversion(Pass) 전략을 거쳐 Backend로 넘긴다.
Optimizer의 대략적인 워크플로는 아래와 같다.
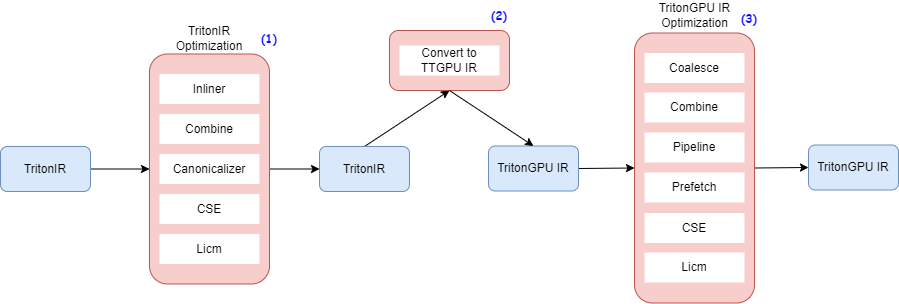 주요 최적화는 크게 세 부분이다.
주요 최적화는 크게 세 부분이다.
중간을 관통하는 데이터 구조는 TritonGPU IR로, 이름 그대로 GPU 관련 정보가 담긴 IR이다.
TritonGPU Dialect는 Triton Dialect에 비해 GPU 하드웨어 관련 Op와 Type이 추가된 것이 핵심이다.
주요 Op는 다음과 같다.
async_wait(N:int) -> (): PTX의 cp.async.wait_group N 명령어에 직접 대응alloc_tensor()->Tensor: shared memory에 위치한 tensor를 allocate함을 표시insert_slice_async(slice:PtrTensor, dst:Tensor, index:int, mask:i1 ...) -> Tensor: (alloc_tensor op가 만든, shared memory 상의) tensor에 slice를 비동기적으로 삽입함을 표시convert_layout(src:Tensor)->Tensor: Tensor의 data layout을 변환앞의 세 Op는 주로 Pipeline과 Prefetch 최적화(아래 Pass 절에서 설명)에 사용되며, convert_layout Op는 TritonGPU Dialect의 Type 시스템에서 매우 중요하다. 다음 두 소절에서 자세히 설명한다.
Data layout은 TritonGPU Dialect의 Type 시스템 핵심으로, 데이터(각 계층 메모리의 Tensor)와 thread 사이의 매핑 관계를 결정한다.
현재 Triton에는 다음과 같은 종류가 있다.
Blocked Layout은 스레드 간에 workload를 균등 분배하는 경우를 나타내며, 각 스레드는 메모리 상 연속적인 데이터 블록을 소유하여 처리한다.
다음 세 필드로 스레드와 데이터 사이의 매핑을 결정한다.
코드의 예시는 다음과 같다.
For example, a row-major coalesced layout may partition a 16x16 tensor over 2 warps (i.e. 64 threads) as follows.
[ 0 0 1 1 2 2 3 3 ; 32 32 33 33 34 34 35 35 ]
[ 0 0 1 1 2 2 3 3 ; 32 32 33 33 34 34 35 35 ]
[ 4 4 5 5 6 6 7 7 ; 36 36 37 37 38 38 39 39 ]
[ 4 4 5 5 6 6 7 7 ; 36 36 37 37 38 38 39 39 ]
...
[ 28 28 29 29 30 30 31 31 ; 60 60 61 61 62 62 63 63 ]
[ 28 28 29 29 30 30 31 31 ; 60 60 61 61 62 62 63 63 ]
for
#triton_gpu.blocked_layout<{
sizePerThread = {2, 2}
threadsPerWarp = {8, 4}
warpsPerCTA = {1, 2}
}>
Shared Layout은 shared memory에서의 데이터 접근 특성(예: swizzle 접근의 파라미터)을 나타낸다.
포함 필드는 다음과 같다.
여기서 vec, perPhase, maxPhase는 bank conflict를 피하기 위한 swizzle 연산에 필요한 파라미터다.
코드 예시:
In order to avoid shared memory bank conflicts, elements may be swizzled
in memory. For example, a swizzled row-major layout could store its data
as follows:
A_{0, 0} A_{0, 1} A_{0, 2} A_{0, 3} ... [phase 0] \ per_phase = 2
A_{1, 0} A_{1, 1} A_{1, 2} A_{1, 3} ... [phase 0] /
groups of vec=2 elements
are stored contiguously
_ _ _ _ /\_ _ _ _
A_{2, 2} A_{2, 3} A_{2, 0} A_{2, 1} ... [phase 1] \ per phase = 2
A_{3, 2} A_{3, 3} A_{3, 0} A_{3, 1} ... [phase 1] /
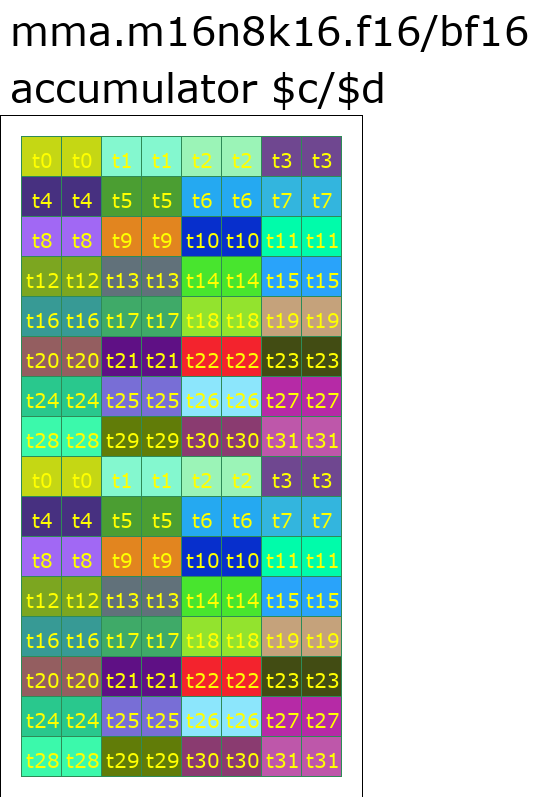
말 그대로 MMA Layout은 Tensor Core의 MMA 명령 결과의 데이터 레이아웃을 나타낸다. 예컨대 Ampere에 대응하는 MMA Layout의 데이터 배치는 PTX 명령 mma.m16n8k16의 C, D 배치와 대체로 대응한다.
MMA Layout의 주요 필드는 두 가지다.
version: TensorCore 버전
warpsPerCTA아래는 FP16 정밀도, version=2(즉 mma.m16n8k16 명령으로 매핑)의 Accumulators(C 또는 D)의 데이터 배치 예시다.
DotOperand Layout은 Triton의 DotOp 입력의 레이아웃을 나타낸다.
주요 정보는 다음과 같다.
opIdx: Operand의 ID
opIdx=0: DotOp의 $aopIdx=1: DotOp의 $bparent: 해당 MMA Layout을 저장. DotOperand의 데이터 배치는 MMA Layout(만약 DotOp가 MMA 명령으로 lower된다면) 혹은 Blocked Layout(DotOp가 FMA 명령으로 lower된다면)에 의해 간접적으로 결정될 수 있다.편의를 위해 MMA Layout 중 mma.m16n8k16.f16 명령을 예로 든다.
version=2warpsPerCTA=[8,4]
Slice Layout은 단일 차원에서의 데이터 역방향 인덱싱을 나타낸다.
말 그대로 ConvertLayoutOp는 Tensor를 한 data layout에서 다른 data layout으로 변환한다. data layout은 TensorType의 일부이므로, 타입(그 중 layout)이 변환되어야 하는 상황이 자연스럽게 발생하며, 이를 담당하는 것이 ConvertLayoutOp다.
위의 Data Layout들을 바탕으로, 가장 단순한 MatMul의 IR을 보자.
#blocked0 = #triton_gpu.blocked<{sizePerThread = [1, 8], threadsPerWarp = [16, 2], warpsPerCTA = [1, 1], order = [1, 0]}>
#blocked1 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [4, 8], warpsPerCTA = [1, 1], order = [1, 0]}>
#mma = #triton_gpu.mma<{version = 2, warpsPerCTA = [1, 1]}>
// ...
%37 = tt.load %arg8 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16xf16, #blocked0>
%38 = tt.load %arg9 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8xf16, #blocked1>
%39 = triton_gpu.convert_layout %37 : (tensor<16x16xf16, #blocked0>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>
%40 = triton_gpu.convert_layout %38 : (tensor<16x8xf16, #blocked1>) -> tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>
%41 = tt.dot %39, %40, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>> * tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>> -> tensor<16x8xf32, #mma>
// ...
위는 전형적인 MatMul 중 한 단계의 TritonGPU IR을 발췌한 것으로, 비교적 직관적이다. #blocked0, #blocked1, #mma 세 가지 layout을 정의한 뒤, tt.load로 DotOp의 두 operand를 GEMM에서 register file로 불러온다. 이후 두 번의 triton_gpu.convert_layout으로 layout을 DotOp가 필요로 하는 #triton_gpu.dot_op로 변환한다.
여기서 몇 가지 전형적인 data layout 변환과 특징을 열거한다.
#shared -> #blocked: 보통 shared memory에서 register file로 데이터를 load함을 의미하며, swizzle을 고려해야 한다.#blocked -> #shared: register file의 데이터를 shared memory로 저장함을 의미하며, 위와 동일한 swizzle 방식을 사용해야 한다.#mma -> #blocked: 보통 DotOp의 출력을 더 단순한 layout으로 변환해 추가 계산을 이어가기 위함. 스레드 간 데이터 전달이 수반되어 보통 shared memory를 한 번 경유한다.#blocked -> #dot_operand: DotOp의 입력으로 변환. 이 단계에서도 shared memory 경유가 필요할 수 있다.Triton은 거의 모든 임의의 data layout 간 변환을 구현하고 있으며, 물론 변환 비용은 동일하지 않다(shared memory 사용 여부, register 증감량 등 고려). 이러한 변환 비용은 Optimizer에서 함께 고려된다.
TritonIR 상의 최적화는 계산 자체의, 하드웨어 무관 최적화로 다음과 같은 Pass를 포함한다.
select(cond, load(ptrs, broadcast(cond), ???), other) => load(ptrs, broadcast(cond), other)TritonGPU IR 상의 최적화는 계산 자체 최적화에 더해 GPU 하드웨어 관련 최적화가 추가된다. 구체 Pass 목록은 다음과 같다.
Pipeline Pass는 다음 소절의 Prefetch Pass와 짝을 이뤄 DotOp(mma 명령)의 operand를 위한 IO 최적화를 제공한다.
Pipeline 최적화는 주로 DotOp에서 GEMM→SMEM 사이 데이터 복사에 대해 Double Buffer 혹은 N-Buffer 최적화를 자동 수행한다.
가장 간단한 Double Buffer의 의사 코드는 다음과 같다.
A = alloc_tensor(shape=[2*16,16])
# cp.async & cp.async.commit_group
A = insert_slice_async(A, ptr0, 0)
B = alloc_tensor(shape=[2*16,8])
B = insert_slice_async(B, ptr1, 0)
A = insert_slice_async(A, ptr00, 1)
B = insert_slice_async(B, ptr11, 0)
async_wait(num=2) # cp.async.wait_group
A_slice0 = extract_slice(A, offset=(0,0,0), size=(1,16,16))
B_slice0 = extract_slice(B, offset=(0,0,0), size=(1,16,8))
for i in range(...):
a = ldmatrix(A_slice0)
b = ldmatrix(B_slice0)
c = dot(a, b)
offset = (i+1) % 2
A = insert_slice_async(A, ptr2, offset)
B = insert_slice_async(B, ptr3, offset)
async_wait(num=2)
A_slice0 = extract_slice(A, offset=(offset,0,0), size=(1,16,16))
B_slice0 = extract_slice(B, offset=(offset,0,0), size=(1,16,8))
여기서,
alloc_tensor는 대략 triton_gpu.alloc_tensor에 대응insert_slice_async는 triton_gpu.insert_slice_async에 대응. Tensor에 slice를 비동기 삽입함을 의미하며, cp.async 명령으로 구현된 비동기tensor.extract_slice는 Tensor에서 slice를 읽어옴async_wait의 의미는 cp.async.wait_group 명령에 대응Prefetch의 로직은 Pipeline Pass와 거의 유사하며, 이 역시 Double/N Buffer 최적화다. 차이는 SMEM→register file의 데이터 이동을 담당한다는 점이다. IR 표현은 triton_gpu.convert_layout %37 : (tensor<16x16xf16, #blocked0>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>이며, 최종적으로 매핑되는 핵심 명령은 ldmatrix다.
Triton의 Backend는 미시적/거시적 두 관점으로 나눠 볼 수 있다.
TritonGPU IR -> LLVM Dialect 과정. 참고로 LLVM Dialect는 MLIR 체계의 한 표현으로, 이후 자동으로 LLVM IR로 낮춰질 수 있다.여기서는 미시적 관점만 소개한다. 거시적 관점의 대부분은 LLVM 커뮤니티나 CUDA 도구가 자동으로 처리한다.
Triton의 Backend는 전형적인 MLIR Lowering으로, TritonGPU IR의 각 Op를 개별적으로 OpConversion 하는 것이 주된 내용이다. 다만 고성능과 코드 생성 산출물의 제어 가능성을 위해, Triton은 LLVM 단계에서 PTX 인라인 어셈블리를 대량으로 삽입한다(아래 소개). 또한 대부분 Op의 Lowering은 상당히 규칙적이며, 아래에서는 Dot 명령의 Lowering을 간략히 설명한다.
Triton에서 인라인 어셈을 사용하는 이유는 대략 다음과 같다.
gpu, nvgpu dialect에 아직 충분히 마련되어 있지 않다.Triton에는 인라인 어셈용 간단한 래퍼가 있으며, 가장 단순한 cp.async.wait_group 호출은 다음과 비슷하다.
PTXBuilder ptxBuilder;
auto &asyncWaitOp = *ptxBuilder.create<>("cp.async.wait_group");
auto num = op->getAttrOfType<IntegerAttr>("num").getInt();
asyncWaitOp(ptxBuilder.newConstantOperand(num));
좀 더 복잡한 ld의 다양한 파라미터 조합은 다음과 같다.
auto &ld = ptxBuilder.create<>("ld")
->o("volatile", op.getIsVolatile())
.global()
.o("ca", op.getCache() == triton::CacheModifier::CA)
.o("cg", op.getCache() == triton::CacheModifier::CG)
.o("L1::evict_first",
op.getEvict() == triton::EvictionPolicy::EVICT_FIRST)
.o("L1::evict_last",
op.getEvict() == triton::EvictionPolicy::EVICT_LAST)
.o("L1::cache_hint", hasL2EvictPolicy)
.v(nWords)
.b(width);
ReduceOp 등 layout과 결합이 많이 필요한 Op와 달리, DotOp의 Lowering은 규칙이 매우 명확하다.
Backend에서 하나의 Dot이 거치는 단계와 Op는 대략 다음과 같다.
| 단계 | Op | 레이아웃 | |
|---|---|---|---|
| 2 | $a, $b의 tile을 SMEM으로 Load | triton_gpu.insert_slice_async | #shared |
| 3 | SMEM에서 Register file로 Load | tensor.extract_slice | #dot_op |
| 4 | MMA 실행, 결과는 Register file에 존재 | tt.dot | #mma |
즉, MMA 명령과 직접 관련된 것은 사실 4단계뿐이다. 필요한 두 인자(a, b)는 이미 tensor.extract_slice로 Register file에 복사되어 있어 Ampere의 mma 명령 요구사항을 바로 만족한다.
Ampere 아키텍처에서 하나의 DotOp는 여러 개의 mma 명령으로 매핑된다. 아래는 FP16의 mma.m16n8k16 명령을 예로 든다. 구체 작업 설정은 다음과 같다.
mma.m16n8k16 명령의 크기는 M=16, N=8, K=16이므로 하나의 타일은 m, n, k 방향으로 2x2x1로 전개되어 총 4개의 mma.m16n8k16 명령이 필요하다.결국 다음과 비슷한 코드가 된다.
for (unsigned k = 0; k < numK; ++k)
for (unsigned m = 0; m < numM; ++m)
for (unsigned n = 0; n < numN; ++n) {
callMMA(m, n, k);
}
여기서 numM, numN, numK는 각각 2, 2, 1에 대응한다.
callMMA의 코드는 앞서 말한 InlineAsm과 유사하며, 다음과 같다.
auto mma = builder.create("mma.sync.aligned.m8n8k4")
->o(isARow ? "row" : "col")
.o(isBRow ? "row" : "col")
.o("f32.f16.f16.f32");
mma(resOprs, AOprs, BOprs, COprs);
아래는 전형적인 GEMM이 Triton의 컴파일 파이프라인을 거치며 IR이 변하는 과정을 나열한다.
def matmul_kernel(
a_ptr, b_ptr, c_ptr,
stride_am, stride_ak,
stride_bk, stride_bn,
stride_cm, stride_cn,
M: tl.constexpr, N: tl.constexpr, K: tl.constexpr,
BLOCK_SIZE_M: tl.constexpr, BLOCK_SIZE_N: tl.constexpr,
BLOCK_SIZE_K: tl.constexpr,
):
offs_m = tl.arange(0, BLOCK_SIZE_M)
offs_n = tl.arange(0, BLOCK_SIZE_N)
offs_k = tl.arange(0, BLOCK_SIZE_K)
a_ptrs = a_ptr + offs_m[:, None] * stride_am + offs_k[None, :] * stride_ak
b_ptrs = b_ptr + offs_k[:, None] * stride_bk + offs_n[None, :] * stride_bn
accumulator = tl.zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=tl.float32)
for k in range(0, K, BLOCK_SIZE_K):
a = tl.load(a_ptrs)
b = tl.load(b_ptrs)
accumulator += tl.dot(a, b)
a_ptrs += BLOCK_SIZE_K * stride_ak
b_ptrs += BLOCK_SIZE_K * stride_bk
c_ptrs = c_ptr + offs_m[:, None] * stride_cm + offs_n[None, :] * stride_cn
tl.store(c_ptrs, accumulator)
이 단계는 Python 코드를 바로 Triton IR로 번역한 것이다.
func public @matmul_kernel_0d1d2d3d4c56c78c(%arg0: !tt.ptr<f16> {tt.divisibility = 16 : i32}, %arg1: !tt.ptr<f16> {tt.divisibility = 16 : i32}, %arg2: !tt.ptr<f32> {tt.divisibility = 16 : i32}, %arg3: i32 {tt.divisibility = 16 : i32}, %arg4: i32, %arg5: i32) {
%cst = arith.constant dense<0.000000e+00> : tensor<16x8xf32>
%c0 = arith.constant 0 : index
%c64 = arith.constant 64 : index
%c16 = arith.constant 16 : index
%cst_0 = arith.constant dense<16> : tensor<16x16xi32>
%c16_i32 = arith.constant 16 : i32
%0 = tt.make_range {end = 16 : i32, start = 0 : i32} : tensor<16xi32>
%1 = tt.make_range {end = 8 : i32, start = 0 : i32} : tensor<8xi32>
%2 = tt.expand_dims %0 {axis = 1 : i32} : (tensor<16xi32>) -> tensor<16x1xi32>
%3 = tt.splat %arg3 : (i32) -> tensor<16x1xi32>
%4 = arith.muli %2, %3 : tensor<16x1xi32>
%5 = tt.splat %arg0 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>>
%6 = tt.addptr %5, %4 : tensor<16x1x!tt.ptr<f16>>
%7 = tt.expand_dims %0 {axis = 0 : i32} : (tensor<16xi32>) -> tensor<1x16xi32>
%8 = tt.broadcast %6 : (tensor<16x1x!tt.ptr<f16>>) -> tensor<16x16x!tt.ptr<f16>>
%9 = tt.broadcast %7 : (tensor<1x16xi32>) -> tensor<16x16xi32>
%10 = tt.addptr %8, %9 : tensor<16x16x!tt.ptr<f16>>
%11 = tt.splat %arg4 : (i32) -> tensor<16x1xi32>
%12 = arith.muli %2, %11 : tensor<16x1xi32>
%13 = tt.splat %arg1 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>>
%14 = tt.addptr %13, %12 : tensor<16x1x!tt.ptr<f16>>
%15 = tt.expand_dims %1 {axis = 0 : i32} : (tensor<8xi32>) -> tensor<1x8xi32>
%16 = tt.broadcast %14 : (tensor<16x1x!tt.ptr<f16>>) -> tensor<16x8x!tt.ptr<f16>>
%17 = tt.broadcast %15 : (tensor<1x8xi32>) -> tensor<16x8xi32>
%18 = tt.addptr %16, %17 : tensor<16x8x!tt.ptr<f16>>
%19:3 = scf.for %arg6 = %c0 to %c64 step %c16 iter_args(%arg7 = %cst, %arg8 = %10, %arg9 = %18) -> (tensor<16x8xf32>, tensor<16x16x!tt.ptr<f16>>, tensor<16x8x!tt.ptr<f16>>) {
%26 = tt.load %arg8 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16xf16>
%27 = tt.load %arg9 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8xf16>
%28 = tt.dot %26, %27, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16> * tensor<16x8xf16> -> tensor<16x8xf32>
%29 = tt.addptr %arg8, %cst_0 : tensor<16x16x!tt.ptr<f16>>
%30 = arith.muli %arg4, %c16_i32 : i32
%31 = tt.splat %30 : (i32) -> tensor<16x8xi32>
%32 = tt.addptr %arg9, %31 : tensor<16x8x!tt.ptr<f16>>
scf.yield %28, %29, %32 : tensor<16x8xf32>, tensor<16x16x!tt.ptr<f16>>, tensor<16x8x!tt.ptr<f16>>
}
%20 = tt.splat %arg5 : (i32) -> tensor<16x1xi32>
%21 = arith.muli %2, %20 : tensor<16x1xi32>
%22 = tt.splat %arg2 : (!tt.ptr<f32>) -> tensor<16x1x!tt.ptr<f32>>
%23 = tt.addptr %22, %21 : tensor<16x1x!tt.ptr<f32>>
%24 = tt.broadcast %23 : (tensor<16x1x!tt.ptr<f32>>) -> tensor<16x8x!tt.ptr<f32>>
%25 = tt.addptr %24, %17 : tensor<16x8x!tt.ptr<f32>>
tt.store %25, %19#0 : tensor<16x8xf32>
return
}
func public @matmul_kernel_0d1d2d3d4c56c78c(%arg0: !tt.ptr<f16> {tt.divisibility = 16 : i32}, %arg1: !tt.ptr<f16> {tt.divisibility = 16 : i32}, %arg2: !tt.ptr<f32> {tt.divisibility = 16 : i32}, %arg3: i32 {tt.divisibility = 16 : i32}, %arg4: i32, %arg5: i32) {
%cst = arith.constant dense<0.000000e+00> : tensor<16x8xf32>
%c0 = arith.constant 0 : index
%c64 = arith.constant 64 : index
%c16 = arith.constant 16 : index
%cst_0 = arith.constant dense<16> : tensor<16x16xi32>
%c16_i32 = arith.constant 16 : i32
%0 = tt.make_range {end = 16 : i32, start = 0 : i32} : tensor<16xi32>
%1 = tt.make_range {end = 8 : i32, start = 0 : i32} : tensor<8xi32>
%2 = tt.expand_dims %0 {axis = 1 : i32} : (tensor<16xi32>) -> tensor<16x1xi32>
%3 = tt.splat %arg3 : (i32) -> tensor<16x1xi32>
%4 = arith.muli %2, %3 : tensor<16x1xi32>
%5 = tt.splat %arg0 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>>
%6 = tt.addptr %5, %4 : tensor<16x1x!tt.ptr<f16>>
%7 = tt.expand_dims %0 {axis = 0 : i32} : (tensor<16xi32>) -> tensor<1x16xi32>
%8 = tt.broadcast %6 : (tensor<16x1x!tt.ptr<f16>>) -> tensor<16x16x!tt.ptr<f16>>
%9 = tt.broadcast %7 : (tensor<1x16xi32>) -> tensor<16x16xi32>
%10 = tt.addptr %8, %9 : tensor<16x16x!tt.ptr<f16>>
%11 = tt.splat %arg4 : (i32) -> tensor<16x1xi32>
%12 = arith.muli %2, %11 : tensor<16x1xi32>
%13 = tt.splat %arg1 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>>
%14 = tt.addptr %13, %12 : tensor<16x1x!tt.ptr<f16>>
%15 = tt.expand_dims %1 {axis = 0 : i32} : (tensor<8xi32>) -> tensor<1x8xi32>
%16 = tt.broadcast %14 : (tensor<16x1x!tt.ptr<f16>>) -> tensor<16x8x!tt.ptr<f16>>
%17 = tt.broadcast %15 : (tensor<1x8xi32>) -> tensor<16x8xi32>
%18 = tt.addptr %16, %17 : tensor<16x8x!tt.ptr<f16>>
%19:3 = scf.for %arg6 = %c0 to %c64 step %c16 iter_args(%arg7 = %cst, %arg8 = %10, %arg9 = %18) -> (tensor<16x8xf32>, tensor<16x16x!tt.ptr<f16>>, tensor<16x8x!tt.ptr<f16>>) {
%26 = tt.load %arg8 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16xf16>
%27 = tt.load %arg9 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8xf16>
%28 = tt.dot %26, %27, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16> * tensor<16x8xf16> -> tensor<16x8xf32>
%29 = tt.addptr %arg8, %cst_0 : tensor<16x16x!tt.ptr<f16>>
%30 = arith.muli %arg4, %c16_i32 : i32
%31 = tt.splat %30 : (i32) -> tensor<16x8xi32>
%32 = tt.addptr %arg9, %31 : tensor<16x8x!tt.ptr<f16>>
scf.yield %28, %29, %32 : tensor<16x8xf32>, tensor<16x16x!tt.ptr<f16>>, tensor<16x8x!tt.ptr<f16>>
}
%20 = tt.splat %arg5 : (i32) -> tensor<16x1xi32>
%21 = arith.muli %2, %20 : tensor<16x1xi32>
%22 = tt.splat %arg2 : (!tt.ptr<f32>) -> tensor<16x1x!tt.ptr<f32>>
%23 = tt.addptr %22, %21 : tensor<16x1x!tt.ptr<f32>>
%24 = tt.broadcast %23 : (tensor<16x1x!tt.ptr<f32>>) -> tensor<16x8x!tt.ptr<f32>>
%25 = tt.addptr %24, %17 : tensor<16x8x!tt.ptr<f32>>
tt.store %25, %19#0 : tensor<16x8xf32>
return
}
이 가운데,
%30 = arith.muli %arg4, %c16_i32 : i32
%31 = tt.splat %30 : (i32) -> tensor<16x8xi32>
이 계산은 입력이 function argument와 constant로, for-loop 내부 변수에 의존하지 않는다. 이론적으로는 밖으로 뺄 수 있다.
LoopInvariantCodeMotion은 MLIR 커뮤니티의 Pass로, 루프와 무관한 변수 계산을 for-loop 밖으로 옮긴다. 위 절의 계산이 실제로 밖으로 이동한 것을 확인할 수 있다.
func public @matmul_kernel_0d1d2d3d4c56c78c(%arg0: !tt.ptr<f16>, %arg1: !tt.ptr<f16>, %arg2: !tt.ptr<f32>, %arg3: i32, %arg4: i32, %arg5: i32) {
%cst = arith.constant dense<0.000000e+00> : tensor<16x8xf32>
%c0 = arith.constant 0 : index
%c64 = arith.constant 64 : index
%c16 = arith.constant 16 : index
%cst_0 = arith.constant dense<16> : tensor<16x16xi32>
%c16_i32 = arith.constant 16 : i32
%0 = tt.make_range {end = 16 : i32, start = 0 : i32} : tensor<16xi32>
%1 = tt.make_range {end = 8 : i32, start = 0 : i32} : tensor<8xi32>
%2 = tt.expand_dims %0 {axis = 1 : i32} : (tensor<16xi32>) -> tensor<16x1xi32>
%3 = tt.splat %arg3 : (i32) -> tensor<16x1xi32>
%4 = arith.muli %2, %3 : tensor<16x1xi32>
%5 = tt.splat %arg0 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>>
%6 = tt.addptr %5, %4 : tensor<16x1x!tt.ptr<f16>>
%7 = tt.expand_dims %0 {axis = 0 : i32} : (tensor<16xi32>) -> tensor<1x16xi32>
%8 = tt.broadcast %6 : (tensor<16x1x!tt.ptr<f16>>) -> tensor<16x16x!tt.ptr<f16>>
%9 = tt.broadcast %7 : (tensor<1x16xi32>) -> tensor<16x16xi32>
%10 = tt.addptr %8, %9 : tensor<16x16x!tt.ptr<f16>>
%11 = tt.splat %arg4 : (i32) -> tensor<16x1xi32>
%12 = arith.muli %2, %11 : tensor<16x1xi32>
%13 = tt.splat %arg1 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>>
%14 = tt.addptr %13, %12 : tensor<16x1x!tt.ptr<f16>>
%15 = tt.expand_dims %1 {axis = 0 : i32} : (tensor<8xi32>) -> tensor<1x8xi32>
%16 = tt.broadcast %14 : (tensor<16x1x!tt.ptr<f16>>) -> tensor<16x8x!tt.ptr<f16>>
%17 = tt.broadcast %15 : (tensor<1x8xi32>) -> tensor<16x8xi32>
%18 = tt.addptr %16, %17 : tensor<16x8x!tt.ptr<f16>>
%19 = arith.muli %arg4, %c16_i32 : i32
%20 = tt.splat %19 : (i32) -> tensor<16x8xi32>
%21:3 = scf.for %arg6 = %c0 to %c64 step %c16 iter_args(%arg7 = %cst, %arg8 = %10, %arg9 = %18) -> (tensor<16x8xf32>, tensor<16x16x!tt.ptr<f16>>, tensor<16x8x!tt.ptr<f16>>) {
%28 = tt.load %arg8 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16xf16>
%29 = tt.load %arg9 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8xf16>
%30 = tt.dot %28, %29, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16> * tensor<16x8xf16> -> tensor<16x8xf32>
%31 = tt.addptr %arg8, %cst_0 : tensor<16x16x!tt.ptr<f16>>
%32 = tt.addptr %arg9, %20 : tensor<16x8x!tt.ptr<f16>>
scf.yield %30, %31, %32 : tensor<16x8xf32>, tensor<16x16x!tt.ptr<f16>>, tensor<16x8x!tt.ptr<f16>>
}
%22 = tt.splat %arg5 : (i32) -> tensor<16x1xi32>
%23 = arith.muli %2, %22 : tensor<16x1xi32>
%24 = tt.splat %arg2 : (!tt.ptr<f32>) -> tensor<16x1x!tt.ptr<f32>>
%25 = tt.addptr %24, %23 : tensor<16x1x!tt.ptr<f32>>
%26 = tt.broadcast %25 : (tensor<16x1x!tt.ptr<f32>>) -> tensor<16x8x!tt.ptr<f32>>
%27 = tt.addptr %26, %17 : tensor<16x8x!tt.ptr<f32>>
tt.store %27, %21#0 : tensor<16x8xf32>
return
}
이 단계에서는 원래의 하드웨어 무관 Triton IR에 GPU 관련 data layout 및 operation이 추가된다.
#blocked0 = #triton_gpu.blocked<{sizePerThread = [1], threadsPerWarp = [16], warpsPerCTA = [1], order = [0]}>
#blocked1 = #triton_gpu.blocked<{sizePerThread = [1], threadsPerWarp = [8], warpsPerCTA = [1], order = [0]}>
#blocked2 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [16, 1], warpsPerCTA = [1, 1], order = [0, 1]}>
#blocked3 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [1, 16], warpsPerCTA = [1, 1], order = [0, 1]}>
#blocked4 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [16, 2], warpsPerCTA = [1, 1], order = [0, 1]}>
#blocked5 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [1, 8], warpsPerCTA = [1, 1], order = [0, 1]}>
module attributes {"triton_gpu.num-warps" = 1 : i32} {
func public @matmul_kernel_0d1d2d3d4c56c78c(%arg0: !tt.ptr<f16>, %arg1: !tt.ptr<f16>, %arg2: !tt.ptr<f32>, %arg3: i32, %arg4: i32, %arg5: i32) {
%cst = arith.constant dense<0.000000e+00> : tensor<16x8xf32, |\colorbox{yellow}{\strut #blocked4}|>
%c0 = arith.constant 0 : index
%c64 = arith.constant 64 : index
%c16 = arith.constant 16 : index
%cst_0 = arith.constant dense<16> : tensor<16x16xi32, #blocked4>
%c16_i32 = arith.constant 16 : i32
%0 = tt.make_range {end = 16 : i32, start = 0 : i32} : tensor<16xi32, #blocked0>
%1 = tt.make_range {end = 8 : i32, start = 0 : i32} : tensor<8xi32, #blocked1>
%2 = triton_gpu.convert_layout %0 : (tensor<16xi32, #blocked0>) -> tensor<16xi32, #triton_gpu.slice<{dim = 1, parent = #blocked2}>>
%3 = tt.expand_dims %2 {axis = 1 : i32} : (tensor<16xi32, #triton_gpu.slice<{dim = 1, parent = #blocked2}>>) -> tensor<16x1xi32, #blocked2>
%4 = tt.splat %arg3 : (i32) -> tensor<16x1xi32, #blocked2>
%5 = arith.muli %3, %4 : tensor<16x1xi32, #blocked2>
%6 = tt.splat %arg0 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>, #blocked2>
%7 = tt.addptr %6, %5 : tensor<16x1x!tt.ptr<f16>, #blocked2>
%8 = triton_gpu.convert_layout %0 : (tensor<16xi32, #blocked0>) -> tensor<16xi32, #triton_gpu.slice<{dim = 0, parent = #blocked3}>>
%9 = tt.expand_dims %8 {axis = 0 : i32} : (tensor<16xi32, #triton_gpu.slice<{dim = 0, parent = #blocked3}>>) -> tensor<1x16xi32, #blocked3>
%10 = tt.broadcast %7 : (tensor<16x1x!tt.ptr<f16>, #blocked2>) -> tensor<16x16x!tt.ptr<f16>, #blocked2>
%11 = triton_gpu.convert_layout %10 : (tensor<16x16x!tt.ptr<f16>, #blocked2>) -> tensor<16x16x!tt.ptr<f16>, #blocked4>
%12 = tt.broadcast %9 : (tensor<1x16xi32, #blocked3>) -> tensor<16x16xi32, #blocked3>
%13 = triton_gpu.convert_layout %12 : (tensor<16x16xi32, #blocked3>) -> tensor<16x16xi32, #blocked4>
%14 = tt.addptr %11, %13 : tensor<16x16x!tt.ptr<f16>, #blocked4>
%15 = tt.splat %arg4 : (i32) -> tensor<16x1xi32, #blocked2>
%16 = arith.muli %3, %15 : tensor<16x1xi32, #blocked2>
%17 = tt.splat %arg1 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>, #blocked2>
%18 = tt.addptr %17, %16 : tensor<16x1x!tt.ptr<f16>, #blocked2>
%19 = triton_gpu.convert_layout %1 : (tensor<8xi32, #blocked1>) -> tensor<8xi32, #triton_gpu.slice<{dim = 0, parent = #blocked5}>>
%20 = tt.expand_dims %19 {axis = 0 : i32} : (tensor<8xi32, #triton_gpu.slice<{dim = 0, parent = #blocked5}>>) -> tensor<1x8xi32, #blocked5>
%21 = tt.broadcast %18 : (tensor<16x1x!tt.ptr<f16>, #blocked2>) -> tensor<16x8x!tt.ptr<f16>, #blocked2>
%22 = triton_gpu.convert_layout %21 : (tensor<16x8x!tt.ptr<f16>, #blocked2>) -> tensor<16x8x!tt.ptr<f16>, #blocked4>
%23 = tt.broadcast %20 : (tensor<1x8xi32, #blocked5>) -> tensor<16x8xi32, #blocked5>
%24 = triton_gpu.convert_layout %23 : (tensor<16x8xi32, #blocked5>) -> tensor<16x8xi32, #blocked4>
%25 = tt.addptr %22, %24 : tensor<16x8x!tt.ptr<f16>, #blocked4>
%26 = arith.muli %arg4, %c16_i32 : i32
%27 = tt.splat %26 : (i32) -> tensor<16x8xi32, #blocked4>
%28:3 = scf.for %arg6 = %c0 to %c64 step %c16 iter_args(%arg7 = %cst, %arg8 = %14, %arg9 = %25) -> (tensor<16x8xf32, #blocked4>, tensor<16x16x!tt.ptr<f16>, #blocked4>, tensor<16x8x!tt.ptr<f16>, #blocked4>) {
%36 = tt.load %arg8 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16xf16, #blocked4>
%37 = tt.load %arg9 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8xf16, #blocked4>
%38 = triton_gpu.convert_layout %36 : (tensor<16x16xf16, #blocked4>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #blocked4}>>
%39 = triton_gpu.convert_layout %37 : (tensor<16x8xf16, #blocked4>) -> tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #blocked4}>>
%40 = tt.dot %38, %39, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #blocked4}>> * tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #blocked4}>> -> tensor<16x8xf32, #blocked4>
%41 = tt.addptr %arg8, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked4>
%42 = tt.addptr %arg9, %27 : tensor<16x8x!tt.ptr<f16>, #blocked4>
scf.yield %40, %41, %42 : tensor<16x8xf32, #blocked4>, tensor<16x16x!tt.ptr<f16>, #blocked4>, tensor<16x8x!tt.ptr<f16>, #blocked4>
}
%29 = tt.splat %arg5 : (i32) -> tensor<16x1xi32, #blocked2>
%30 = arith.muli %3, %29 : tensor<16x1xi32, #blocked2>
%31 = tt.splat %arg2 : (!tt.ptr<f32>) -> tensor<16x1x!tt.ptr<f32>, #blocked2>
%32 = tt.addptr %31, %30 : tensor<16x1x!tt.ptr<f32>, #blocked2>
%33 = tt.broadcast %32 : (tensor<16x1x!tt.ptr<f32>, #blocked2>) -> tensor<16x8x!tt.ptr<f32>, #blocked2>
%34 = triton_gpu.convert_layout %33 : (tensor<16x8x!tt.ptr<f32>, #blocked2>) -> tensor<16x8x!tt.ptr<f32>, #blocked4>
%35 = tt.addptr %34, %24 : tensor<16x8x!tt.ptr<f32>, #blocked4>
tt.store %35, %28#0 : tensor<16x8xf32, #blocked4>
return
}
여기서 눈에 띄는 점은 다음과 같다.
%40은 mma layout이어야 하나, 이 단계에서는 아직 blocked layout이다. 이는 다음 절에서 rewrite된다.%38, %39 등의 layout은 dot_op<mma>여야 하지만 mma layout이 아직 주어지지 않아 dot_op<blocked> 상태다.이 단계에서는 여러 Op 패턴 rewrite가 포함되며, 직접적인 변화는 다음과 같다.
convert_layout 삽입#blocked0 = #triton_gpu.blocked<{sizePerThread = [1, 8], threadsPerWarp = [16, 2], warpsPerCTA = [1, 1], order = [1, 0]}>
#blocked1 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [4, 8], warpsPerCTA = [1, 1], order = [1, 0]}>
#mma = #triton_gpu.mma<{version = 2, warpsPerCTA = [1, 1]}>
module attributes {"triton_gpu.num-warps" = 1 : i32} {
func public @matmul_kernel_0d1d2d3d4c56c78c(%arg0: !tt.ptr<f16> {tt.divisibility = 16 : i32}, %arg1: !tt.ptr<f16> {tt.divisibility = 16 : i32}, %arg2: !tt.ptr<f32> {tt.divisibility = 16 : i32}, %arg3: i32 {tt.divisibility = 16 : i32}, %arg4: i32, %arg5: i32) {
%c0 = arith.constant 0 : index
%c64 = arith.constant 64 : index
%c16 = arith.constant 16 : index
%c16_i32 = arith.constant 16 : i32
%cst = arith.constant dense<0.000000e+00> : tensor<16x8xf32, #mma>
%cst_0 = arith.constant dense<16> : tensor<16x16xi32, #blocked0>
%0 = tt.make_range {end = 16 : i32, start = 0 : i32} : tensor<16xi32, #triton_gpu.slice<{dim = 1, parent = #blocked0}>>
%1 = tt.make_range {end = 16 : i32, start = 0 : i32} : tensor<16xi32, #triton_gpu.slice<{dim = 1, parent = #blocked1}>>
%2 = tt.make_range {end = 16 : i32, start = 0 : i32} : tensor<16xi32, #triton_gpu.slice<{dim = 1, parent = #blocked1}>>
%3 = tt.splat %arg3 : (i32) -> tensor<16x1xi32, #blocked0>
%4 = tt.splat %arg0 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>, #blocked0>
%5 = tt.make_range {end = 16 : i32, start = 0 : i32} : tensor<16xi32, #triton_gpu.slice<{dim = 0, parent = #blocked0}>>
%6 = tt.expand_dims %0 {axis = 1 : i32} : (tensor<16xi32, #triton_gpu.slice<{dim = 1, parent = #blocked0}>>) -> tensor<16x1xi32, #blocked0>
%7 = arith.muli %6, %3 : tensor<16x1xi32, #blocked0>
%8 = tt.addptr %4, %7 : tensor<16x1x!tt.ptr<f16>, #blocked0>
%9 = tt.broadcast %8 : (tensor<16x1x!tt.ptr<f16>, #blocked0>) -> tensor<16x16x!tt.ptr<f16>, #blocked0>
%10 = tt.expand_dims %5 {axis = 0 : i32} : (tensor<16xi32, #triton_gpu.slice<{dim = 0, parent = #blocked0}>>) -> tensor<1x16xi32, #blocked0>
%11 = tt.broadcast %10 : (tensor<1x16xi32, #blocked0>) -> tensor<16x16xi32, #blocked0>
%12 = tt.splat %arg4 : (i32) -> tensor<16x1xi32, #blocked1>
%13 = tt.splat %arg1 : (!tt.ptr<f16>) -> tensor<16x1x!tt.ptr<f16>, #blocked1>
%14 = tt.make_range {end = 8 : i32, start = 0 : i32} : tensor<8xi32, #triton_gpu.slice<{dim = 0, parent = #blocked1}>>
%15 = tt.make_range {end = 8 : i32, start = 0 : i32} : tensor<8xi32, #triton_gpu.slice<{dim = 0, parent = #blocked1}>>
%16 = tt.expand_dims %1 {axis = 1 : i32} : (tensor<16xi32, #triton_gpu.slice<{dim = 1, parent = #blocked1}>>) -> tensor<16x1xi32, #blocked1>
%17 = arith.muli %16, %12 : tensor<16x1xi32, #blocked1>
%18 = tt.addptr %13, %17 : tensor<16x1x!tt.ptr<f16>, #blocked1>
%19 = tt.broadcast %18 : (tensor<16x1x!tt.ptr<f16>, #blocked1>) -> tensor<16x8x!tt.ptr<f16>, #blocked1>
%20 = tt.expand_dims %14 {axis = 0 : i32} : (tensor<8xi32, #triton_gpu.slice<{dim = 0, parent = #blocked1}>>) -> tensor<1x8xi32, #blocked1>
%21 = tt.broadcast %20 : (tensor<1x8xi32, #blocked1>) -> tensor<16x8xi32, #blocked1>
%22 = tt.expand_dims %15 {axis = 0 : i32} : (tensor<8xi32, #triton_gpu.slice<{dim = 0, parent = #blocked1}>>) -> tensor<1x8xi32, #blocked1>
%23 = tt.broadcast %22 : (tensor<1x8xi32, #blocked1>) -> tensor<16x8xi32, #blocked1>
%24 = arith.muli %arg4, %c16_i32 : i32
%25 = tt.splat %24 : (i32) -> tensor<16x8xi32, #blocked1>
%26 = tt.addptr %9, %11 : tensor<16x16x!tt.ptr<f16>, #blocked0>
%27 = tt.addptr %19, %21 : tensor<16x8x!tt.ptr<f16>, #blocked1>
%28:3 = scf.for %arg6 = %c0 to %c64 step %c16 iter_args(%arg7 = %cst, %arg8 = %26, %arg9 = %27) -> (tensor<16x8xf32, #mma>, tensor<16x16x!tt.ptr<f16>, #blocked0>, tensor<16x8x!tt.ptr<f16>, #blocked1>) {
%37 = tt.load %arg8 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16xf16, #blocked0>
%38 = tt.load %arg9 {cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8xf16, #blocked1>
%39 = triton_gpu.convert_layout %37 : (tensor<16x16xf16, #blocked0>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>
%40 = triton_gpu.convert_layout %38 : (tensor<16x8xf16, #blocked1>) -> tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>
%41 = tt.dot %39, %40, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>> * tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>> -> tensor<16x8xf32, #mma>
%42 = tt.addptr %arg8, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
%43 = tt.addptr %arg9, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
scf.yield %41, %42, %43 : tensor<16x8xf32, #mma>, tensor<16x16x!tt.ptr<f16>, #blocked0>, tensor<16x8x!tt.ptr<f16>, #blocked1>
}
%29 = tt.splat %arg5 : (i32) -> tensor<16x1xi32, #blocked1>
%30 = tt.splat %arg2 : (!tt.ptr<f32>) -> tensor<16x1x!tt.ptr<f32>, #blocked1>
%31 = tt.expand_dims %2 {axis = 1 : i32} : (tensor<16xi32, #triton_gpu.slice<{dim = 1, parent = #blocked1}>>) -> tensor<16x1xi32, #blocked1>
%32 = arith.muli %31, %29 : tensor<16x1xi32, #blocked1>
%33 = tt.addptr %30, %32 : tensor<16x1x!tt.ptr<f32>, #blocked1>
%34 = tt.broadcast %33 : (tensor<16x1x!tt.ptr<f32>, #blocked1>) -> tensor<16x8x!tt.ptr<f32>, #blocked1>
%35 = tt.addptr %34, %23 : tensor<16x8x!tt.ptr<f32>, #blocked1>
%36 = triton_gpu.convert_layout %28#0 : (tensor<16x8xf32, #mma>) -> tensor<16x8xf32, #blocked1>
tt.store %35, %36 : tensor<16x8xf32, #blocked1>
return
}
이 단계는 global memory → shared memory 데이터 이동에서 Pipeline 최적화를 수행했다고 볼 수 있다.
#blocked0 = #triton_gpu.blocked<{sizePerThread = [1, 8], threadsPerWarp = [16, 2], warpsPerCTA = [1, 1], order = [1, 0]}>
#blocked1 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [4, 8], warpsPerCTA = [1, 1], order = [1, 0]}>
#mma = #triton_gpu.mma<{version = 2, warpsPerCTA = [1, 1]}>
#shared0 = #triton_gpu.shared<{vec = 8, perPhase = 4, maxPhase = 2, order = [1, 0]}>
#shared1 = #triton_gpu.shared<{vec = 8, perPhase = 8, maxPhase = 1, order = [1, 0]}>
module attributes {"triton_gpu.num-warps" = 1 : i32} {
func public @matmul_kernel_0d1d2d3d4c56c78c(%arg0: !tt.ptr<f16>, %arg1: !tt.ptr<f16>, %arg2: !tt.ptr<f32>, %arg3: i32, %arg4: i32, %arg5: i32) {
...
%28 = arith.cmpi slt, %c0, %c64 : index
%29 = triton_gpu.alloc_tensor : tensor<3x16x16xf16, #shared0>
%30 = tt.splat %28 : (i1) -> tensor<16x16xi1, #blocked0>
%31 = triton_gpu.insert_slice_async %26, %29, %c0_i32, %30 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16x!tt.ptr<f16>, #blocked0> -> tensor<3x16x16xf16, #shared0>
%32 = triton_gpu.alloc_tensor : tensor<3x16x8xf16, #shared1>
%33 = tt.splat %28 : (i1) -> tensor<16x8xi1, #blocked1>
%34 = triton_gpu.insert_slice_async %27, %32, %c0_i32, %33 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8x!tt.ptr<f16>, #blocked1> -> tensor<3x16x8xf16, #shared1>
%35 = tt.addptr %26, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
%36 = tt.addptr %27, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
...
%40 = tt.splat %39 : (i1) -> tensor<16x16xi1, #blocked0>
%41 = triton_gpu.insert_slice_async %35, %31, %37, %40 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16x!tt.ptr<f16>, #blocked0> -> tensor<3x16x16xf16, #shared0>
%42 = tt.splat %39 : (i1) -> tensor<16x8xi1, #blocked1>
%43 = triton_gpu.insert_slice_async %36, %34, %37, %42 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8x!tt.ptr<f16>, #blocked1> -> tensor<3x16x8xf16, #shared1>
%44 = tt.addptr %35, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
%45 = tt.addptr %36, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
%c1_i32_1 = arith.constant 1 : i32
%46 = arith.addi %37, %c1_i32_1 : i32
triton_gpu.async_wait {num = 2 : i32}
%c0_i32_2 = arith.constant 0 : i32
%47 = tensor.extract_slice %41[0, 0, 0] [1, 16, 16] [1, 1, 1] : tensor<3x16x16xf16, #shared0> to tensor<16x16xf16, #shared0>
%48 = tensor.extract_slice %43[0, 0, 0] [1, 16, 8] [1, 1, 1] : tensor<3x16x8xf16, #shared1> to tensor<16x8xf16, #shared1>
%c1_i32_3 = arith.constant 1 : i32
%49 = arith.addi %c0_i32_2, %c1_i32_3 : i32
%50:12 = scf.for %arg6 = %c0 to %c64 step %c16 iter_args(%arg7 = %cst, %arg8 = %26, %arg9 = %27, %arg10 = %41, %arg11 = %43, %arg12 = %47, %arg13 = %48, %arg14 = %45, %arg15 = %44, %arg16 = %38, %arg17 = %46, %arg18 = %49) -> (tensor<16x8xf32, #mma>, tensor<16x16x!tt.ptr<f16>, #blocked0>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<3x16x16xf16, #shared0>, tensor<3x16x8xf16, #shared1>, tensor<16x16xf16, #shared0>, tensor<16x8xf16, #shared1>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<16x16x!tt.ptr<f16>, #blocked0>, index, i32, i32) {
%59 = triton_gpu.convert_layout %arg12 : (tensor<16x16xf16, #shared0>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>
%60 = triton_gpu.convert_layout %arg13 : (tensor<16x8xf16, #shared1>) -> tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>
%61 = tt.dot %59, %60, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>> * tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>> -> tensor<16x8xf32, #mma>
%62 = tt.addptr %arg8, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
%63 = tt.addptr %arg9, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
%64 = arith.addi %arg16, %c16 : index
%65 = arith.cmpi slt, %64, %c64 : index
%c3_i32 = arith.constant 3 : i32
%66 = arith.remsi %arg17, %c3_i32 : i32
%c3_i32_4 = arith.constant 3 : i32
%67 = arith.remsi %arg18, %c3_i32_4 : i32
%68 = arith.index_cast %67 : i32 to index
%69 = tt.splat %65 : (i1) -> tensor<16x16xi1, #blocked0>
%70 = triton_gpu.insert_slice_async %arg15, %arg10, %66, %69 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16x!tt.ptr<f16>, #blocked0> -> tensor<3x16x16xf16, #shared0>
%71 = tt.splat %65 : (i1) -> tensor<16x8xi1, #blocked1>
%72 = triton_gpu.insert_slice_async %arg14, %arg11, %66, %71 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8x!tt.ptr<f16>, #blocked1> -> tensor<3x16x8xf16, #shared1>
%73 = tt.addptr %arg15, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
%74 = tt.addptr %arg14, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
triton_gpu.async_wait {num = 2 : i32}
%75 = tensor.extract_slice %70[%68, 0, 0] [1, 16, 16] [1, 1, 1] : tensor<3x16x16xf16, #shared0> to tensor<16x16xf16, #shared0>
%76 = tensor.extract_slice %72[%68, 0, 0] [1, 16, 8] [1, 1, 1] : tensor<3x16x8xf16, #shared1> to tensor<16x8xf16, #shared1>
%c1_i32_5 = arith.constant 1 : i32
%77 = arith.addi %arg17, %c1_i32_5 : i32
%c1_i32_6 = arith.constant 1 : i32
%78 = arith.addi %arg18, %c1_i32_6 : i32
scf.yield %61, %62, %63, %70, %72, %75, %76, %74, %73, %64, %77, %78 : tensor<16x8xf32, #mma>, tensor<16x16x!tt.ptr<f16>, #blocked0>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<3x16x16xf16, #shared0>, tensor<3x16x8xf16, #shared1>, tensor<16x16xf16, #shared0>, tensor<16x8xf16, #shared1>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<16x16x!tt.ptr<f16>, #blocked0>, index, i32, i32
}
...
return
}
}
#blocked0 = #triton_gpu.blocked<{sizePerThread = [1, 8], threadsPerWarp = [16, 2], warpsPerCTA = [1, 1], order = [1, 0]}>
#blocked1 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [4, 8], warpsPerCTA = [1, 1], order = [1, 0]}>
#mma = #triton_gpu.mma<{version = 2, warpsPerCTA = [1, 1]}>
#shared0 = #triton_gpu.shared<{vec = 8, perPhase = 4, maxPhase = 2, order = [1, 0]}>
#shared1 = #triton_gpu.shared<{vec = 8, perPhase = 8, maxPhase = 1, order = [1, 0]}>
module attributes {"triton_gpu.num-warps" = 1 : i32} {
func public @matmul_kernel_0d1d2d3d4c56c78c(%arg0: !tt.ptr<f16>, %arg1: !tt.ptr<f16>, %arg2: !tt.ptr<f32>, %arg3: i32, %arg4: i32, %arg5: i32) {
...
%28 = arith.cmpi slt, %c0, %c64 : index
%29 = triton_gpu.alloc_tensor : tensor<3x16x16xf16, #shared0>
%30 = tt.splat %28 : (i1) -> tensor<16x16xi1, #blocked0>
%31 = triton_gpu.insert_slice_async %26, %29, %c0_i32, %30 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16x!tt.ptr<f16>, #blocked0> -> tensor<3x16x16xf16, #shared0>
%32 = triton_gpu.alloc_tensor : tensor<3x16x8xf16, #shared1>
%33 = tt.splat %28 : (i1) -> tensor<16x8xi1, #blocked1>
%34 = triton_gpu.insert_slice_async %27, %32, %c0_i32, %33 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8x!tt.ptr<f16>, #blocked1> -> tensor<3x16x8xf16, #shared1>
%35 = tt.addptr %26, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
%36 = tt.addptr %27, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
...
%40 = tt.splat %39 : (i1) -> tensor<16x16xi1, #blocked0>
%41 = triton_gpu.insert_slice_async %35, %31, %37, %40 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16x!tt.ptr<f16>, #blocked0> -> tensor<3x16x16xf16, #shared0>
%42 = tt.splat %39 : (i1) -> tensor<16x8xi1, #blocked1>
%43 = triton_gpu.insert_slice_async %36, %34, %37, %42 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8x!tt.ptr<f16>, #blocked1> -> tensor<3x16x8xf16, #shared1>
%44 = tt.addptr %35, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
%45 = tt.addptr %36, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
%c1_i32_1 = arith.constant 1 : i32
%46 = arith.addi %37, %c1_i32_1 : i32
triton_gpu.async_wait {num = 2 : i32}
%c0_i32_2 = arith.constant 0 : i32
%47 = tensor.extract_slice %41[0, 0, 0] [1, 16, 16] [1, 1, 1] : tensor<3x16x16xf16, #shared0> to tensor<16x16xf16, #shared0>
%48 = tensor.extract_slice %43[0, 0, 0] [1, 16, 8] [1, 1, 1] : tensor<3x16x8xf16, #shared1> to tensor<16x8xf16, #shared1>
%c1_i32_3 = arith.constant 1 : i32
%49 = arith.addi %c0_i32_2, %c1_i32_3 : i32
%50:12 = scf.for %arg6 = %c0 to %c64 step %c16 iter_args(%arg7 = %cst, %arg8 = %26, %arg9 = %27, %arg10 = %41, %arg11 = %43, %arg12 = %47, %arg13 = %48, %arg14 = %45, %arg15 = %44, %arg16 = %38, %arg17 = %46, %arg18 = %49) -> (tensor<16x8xf32, #mma>, tensor<16x16x!tt.ptr<f16>, #blocked0>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<3x16x16xf16, #shared0>, tensor<3x16x8xf16, #shared1>, tensor<16x16xf16, #shared0>, tensor<16x8xf16, #shared1>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<16x16x!tt.ptr<f16>, #blocked0>, index, i32, i32) {
%59 = triton_gpu.convert_layout %arg12 : (tensor<16x16xf16, #shared0>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>
%60 = triton_gpu.convert_layout %arg13 : (tensor<16x8xf16, #shared1>) -> tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>
%61 = tt.dot %59, %60, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>> * tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>> -> tensor<16x8xf32, #mma>
%62 = tt.addptr %arg8, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
%63 = tt.addptr %arg9, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
%64 = arith.addi %arg16, %c16 : index
%65 = arith.cmpi slt, %64, %c64 : index
%c3_i32 = arith.constant 3 : i32
%66 = arith.remsi %arg17, %c3_i32 : i32
%c3_i32_4 = arith.constant 3 : i32
%67 = arith.remsi %arg18, %c3_i32_4 : i32
%68 = arith.index_cast %67 : i32 to index
%69 = tt.splat %65 : (i1) -> tensor<16x16xi1, #blocked0>
%70 = triton_gpu.insert_slice_async %arg15, %arg10, %66, %69 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16x!tt.ptr<f16>, #blocked0> -> tensor<3x16x16xf16, #shared0>
%71 = tt.splat %65 : (i1) -> tensor<16x8xi1, #blocked1>
%72 = triton_gpu.insert_slice_async %arg14, %arg11, %66, %71 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8x!tt.ptr<f16>, #blocked1> -> tensor<3x16x8xf16, #shared1>
%73 = tt.addptr %arg15, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
%74 = tt.addptr %arg14, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
triton_gpu.async_wait {num = 2 : i32}
%75 = tensor.extract_slice %70[%68, 0, 0] [1, 16, 16] [1, 1, 1] : tensor<3x16x16xf16, #shared0> to tensor<16x16xf16, #shared0>
%76 = tensor.extract_slice %72[%68, 0, 0] [1, 16, 8] [1, 1, 1] : tensor<3x16x8xf16, #shared1> to tensor<16x8xf16, #shared1>
%c1_i32_5 = arith.constant 1 : i32
%77 = arith.addi %arg17, %c1_i32_5 : i32
%c1_i32_6 = arith.constant 1 : i32
%78 = arith.addi %arg18, %c1_i32_6 : i32
scf.yield %61, %62, %63, %70, %72, %75, %76, %74, %73, %64, %77, %78 : tensor<16x8xf32, #mma>, tensor<16x16x!tt.ptr<f16>, #blocked0>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<3x16x16xf16, #shared0>, tensor<3x16x8xf16, #shared1>, tensor<16x16xf16, #shared0>, tensor<16x8xf16, #shared1>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<16x16x!tt.ptr<f16>, #blocked0>, index, i32, i32
}
...
return
}
}
이 단계는 Dot 관련 shared memory → registers 데이터 이동에서 Pipeline 최적화를 수행했다고 볼 수 있다.
#blocked0 = #triton_gpu.blocked<{sizePerThread = [1, 8], threadsPerWarp = [16, 2], warpsPerCTA = [1, 1], order = [1, 0]}>
#blocked1 = #triton_gpu.blocked<{sizePerThread = [1, 1], threadsPerWarp = [4, 8], warpsPerCTA = [1, 1], order = [1, 0]}>
#mma = #triton_gpu.mma<{version = 2, warpsPerCTA = [1, 1]}>
#shared0 = #triton_gpu.shared<{vec = 8, perPhase = 4, maxPhase = 2, order = [1, 0]}>
#shared1 = #triton_gpu.shared<{vec = 8, perPhase = 8, maxPhase = 1, order = [1, 0]}>
module attributes {"triton_gpu.num-warps" = 1 : i32} {
func public @matmul_kernel_0d1d2d3d4c56c78c(%arg0: !tt.ptr<f16> {tt.divisibility = 16 : i32}, %arg1: !tt.ptr<f16> {tt.divisibility = 16 : i32}, %arg2: !tt.ptr<f32> {tt.divisibility = 16 : i32}, %arg3: i32 {tt.divisibility = 16 : i32}, %arg4: i32, %arg5: i32) {
...
triton_gpu.async_wait {num = 2 : i32}
%c0_i32_2 = arith.constant 0 : i32
%47 = tensor.extract_slice %41[0, 0, 0] [1, 16, 16] [1, 1, 1] : tensor<3x16x16xf16, #shared0> to tensor<16x16xf16, #shared0>
%48 = tensor.extract_slice %43[0, 0, 0] [1, 16, 8] [1, 1, 1] : tensor<3x16x8xf16, #shared1> to tensor<16x8xf16, #shared1>
%c1_i32_3 = arith.constant 1 : i32
%49 = arith.addi %c0_i32_2, %c1_i32_3 : i32
%50 = tensor.extract_slice %47[0, 0] [16, 16] [1, 1] : tensor<16x16xf16, #shared0> to tensor<16x16xf16, #shared0>
%51 = triton_gpu.convert_layout %50 : (tensor<16x16xf16, #shared0>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>
%52 = tensor.extract_slice %48[0, 0] [16, 8] [1, 1] : tensor<16x8xf16, #shared1> to tensor<16x8xf16, #shared1>
%53 = triton_gpu.convert_layout %52 : (tensor<16x8xf16, #shared1>) -> tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>
%54:14 = scf.for %arg6 = %c0 to %c64 step %c16 iter_args(%arg7 = %cst, %arg8 = %26, %arg9 = %27, %arg10 = %41, %arg11 = %43, %arg12 = %47, %arg13 = %48, %arg14 = %45, %arg15 = %44, %arg16 = %38, %arg17 = %46, %arg18 = %49, %arg19 = %51, %arg20 = %53) -> (tensor<16x8xf32, #mma>, tensor<16x16x!tt.ptr<f16>, #blocked0>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<3x16x16xf16, #shared0>, tensor<3x16x8xf16, #shared1>, tensor<16x16xf16, #shared0>, tensor<16x8xf16, #shared1>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<16x16x!tt.ptr<f16>, #blocked0>, index, i32, i32, tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>, tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>) {
%63 = triton_gpu.convert_layout %arg12 : (tensor<16x16xf16, #shared0>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>
%64 = triton_gpu.convert_layout %arg13 : (tensor<16x8xf16, #shared1>) -> tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>
%65 = tt.dot %63, %64, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>> * tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>> -> tensor<16x8xf32, #mma>
%66 = tt.dot %arg19, %arg20, %arg7 {allowTF32 = true, transA = false, transB = false} : tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>> * tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>> -> tensor<16x8xf32, #mma>
%67 = tt.addptr %arg8, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
%68 = tt.addptr %arg9, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
%69 = arith.addi %arg16, %c16 : index
%70 = arith.cmpi slt, %69, %c64 : index
%c3_i32 = arith.constant 3 : i32
%71 = arith.remsi %arg17, %c3_i32 : i32
%c3_i32_4 = arith.constant 3 : i32
%72 = arith.remsi %arg18, %c3_i32_4 : i32
%73 = arith.index_cast %72 : i32 to index
%74 = tt.splat %70 : (i1) -> tensor<16x16xi1, #blocked0>
%75 = triton_gpu.insert_slice_async %arg15, %arg10, %71, %74 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x16x!tt.ptr<f16>, #blocked0> -> tensor<3x16x16xf16, #shared0>
%76 = tt.splat %70 : (i1) -> tensor<16x8xi1, #blocked1>
%77 = triton_gpu.insert_slice_async %arg14, %arg11, %71, %76 {axis = 0 : i32, cache = 1 : i32, evict = 1 : i32, isVolatile = false} : tensor<16x8x!tt.ptr<f16>, #blocked1> -> tensor<3x16x8xf16, #shared1>
%78 = tt.addptr %arg15, %cst_0 : tensor<16x16x!tt.ptr<f16>, #blocked0>
%79 = tt.addptr %arg14, %25 : tensor<16x8x!tt.ptr<f16>, #blocked1>
triton_gpu.async_wait {num = 2 : i32}
%80 = tensor.extract_slice %75[%73, 0, 0] [1, 16, 16] [1, 1, 1] : tensor<3x16x16xf16, #shared0> to tensor<16x16xf16, #shared0>
%81 = tensor.extract_slice %77[%73, 0, 0] [1, 16, 8] [1, 1, 1] : tensor<3x16x8xf16, #shared1> to tensor<16x8xf16, #shared1>
%c1_i32_5 = arith.constant 1 : i32
%82 = arith.addi %arg17, %c1_i32_5 : i32
%c1_i32_6 = arith.constant 1 : i32
%83 = arith.addi %arg18, %c1_i32_6 : i32
%84 = tensor.extract_slice %80[0, 0] [16, 16] [1, 1] : tensor<16x16xf16, #shared0> to tensor<16x16xf16, #shared0>
%85 = triton_gpu.convert_layout %84 : (tensor<16x16xf16, #shared0>) -> tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>
%86 = tensor.extract_slice %81[0, 0] [16, 8] [1, 1] : tensor<16x8xf16, #shared1> to tensor<16x8xf16, #shared1>
%87 = triton_gpu.convert_layout %86 : (tensor<16x8xf16, #shared1>) -> tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>
scf.yield %65, %67, %68, %75, %77, %80, %81, %79, %78, %69, %82, %83, %85, %87 : tensor<16x8xf32, #mma>, tensor<16x16x!tt.ptr<f16>, #blocked0>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<3x16x16xf16, #shared0>, tensor<3x16x8xf16, #shared1>, tensor<16x16xf16, #shared0>, tensor<16x8xf16, #shared1>, tensor<16x8x!tt.ptr<f16>, #blocked1>, tensor<16x16x!tt.ptr<f16>, #blocked0>, index, i32, i32, tensor<16x16xf16, #triton_gpu.dot_op<{opIdx = 0, parent = #mma}>>, tensor<16x8xf16, #triton_gpu.dot_op<{opIdx = 1, parent = #mma}>>
}
...
return
}
}
MLIR 단계의 마지막은 LLVM dialect로 translate하는 것으로, Triton backend가 삽입한 인라인 어셈을 확인할 수 있다.
module attributes {"triton_gpu.num-warps" = 4 : i32, triton_gpu.shared = 36864 : i32} {
llvm.mlir.global external @global_smem() {addr_space = 3 : i32} : !llvm.array<0 x i8>
llvm.func @matmul_kernel_0d1d2d3d4c5d6c7d8c(%arg0: !llvm.ptr<f16, 1> {tt.divisibility = 16 : i32}, %arg1: !llvm.ptr<f16, 1> {tt.divisibility = 16 : i32}, %arg2: !llvm.ptr<f32, 1> {tt.divisibility = 16 : i32}, %arg3: i32 {tt.divisibility = 16 : i32}, %arg4: i32 {tt.divisibility = 16 : i32}, %arg5: i32 {tt.divisibility = 16 : i32}) attributes {nvvm.kernel = 1 : ui1, nvvm.maxntid = 128 : i32, sym_visibility = "public"} {
%0 = llvm.mlir.addressof @global_smem : !llvm.ptr<array<0 x i8>, 3>
%1 = llvm.bitcast %0 : !llvm.ptr<array<0 x i8>, 3> to !llvm.ptr<i8, 3>
%2 = llvm.mlir.constant(3 : i32) : i32
%3 = llvm.mlir.constant(1 : i32) : i32
%4 = llvm.mlir.constant(0 : i32) : i32
%5 = llvm.mlir.constant(2 : i32) : i32
%6 = llvm.mlir.constant(true) : i1
%7 = llvm.mlir.constant(32 : index) : i32
%8 = llvm.mlir.constant(32 : i32) : i32
%9 = llvm.mlir.constant(0.000000e+00 : f32) : f32
...
%567 = llvm.inline_asm has_side_effects asm_dialect = att operand_attrs = [] "ldmatrix.sync.aligned.m8n8.x4.shared.b16 { $0, $1, $2, $3 }, [ $4 + 0 ];", "=r,=r,=r,=r,r" %566 : (!llvm.ptr<f16, 3>) -> !llvm.struct<(vector<2xf16>, vector<2xf16>, vector<2xf16>, vector<2xf16>)>
...
%765 = llvm.inline_asm has_side_effects asm_dialect = att operand_attrs = [] "mma.sync.aligned.m16n8k16.row.col.f32.f16.f16.f32 { $0, $1, $2, $3 }, { $4, $5, $6, $7 }, { $8, $9 }, { $10, $11, $12, $13 };", "=r,=r,=r,=r,r,r,r,r,r,r,0,1,2,3" %677, %679, %678, %680, %685, %686, %701, %702, %703, %704 : (vector<2xf16>, vector<2xf16>, vector<2xf16>, vector<2xf16>, vector<2xf16>, vector<2xf16>, f32, f32, f32, f32) -> !llvm.struct<(f32, f32, f32, f32)>
...
%1789 = llvm.inline_asm has_side_effects asm_dialect = att operand_attrs = [] "@$5 st.global.v4.b32 [ $4 + 0 ], { $0, $1, $2, $3 };", "r,r,r,r,l,b" %1782, %1784, %1786, %1788, %1449, %6 : (i32, i32, i32, i32, !llvm.ptr<f32, 1>, i1) -> !llvm.void
...