정적 단일 할당(SSA) 형태와 SSA-CFG IR을 직관적으로 소개하고, 기본 블록·지배 관계·지배 경계 같은 그래프 이론 개념을 토대로 의존성/데이터플로 분석, 메모리 올리기(load lifting), 그리고 불필요 결과 제거·CFG 단순화 같은 정리 패스를 설계·설명한다.
If you’ve read anything about compilers in the last two decades or so, you have almost certainly heard of SSA compilers, a popular architecture featured in many optimizing compilers, including ahead-of-time compilers such as LLVM, GCC, Go, CUDA (and various shader compilers), Swift1, and MSVC2, and just-in-time compilers such as HotSpot C23, V84, SpiderMonkey5, LuaJIT, and the Android Runtime6.
SSA는 너무나 대중적이라서, 오늘날 대부분의 컴파일러 프로젝트는 최적화를 위한 다른 IR를 굳이 쓰지 않을 정도다7. 이는 SSA가 컴파일러 최적화가 여러분의 코드를 대상으로 하고 싶어 하는 각종 프로그램 분석과 변환에 놀라울 정도로 민첩하기 때문이다. 그런데 왜 그럴까? 컴파일러를 하지 않는 제 주변 친구들은, 컴파일러가 불투명한 마법의 블랙박스 같다고들 말하고, 문헌에서 흔히 보는 SSA는 뚫고 들어가기 어려운 난해한 것으로 보인다고 한다.
하지만 그렇지 않다! 여러분이 “프로그램이 실제로 무엇을 한다고 생각하는지”를 모두 잊기만 하면, SSA는 사실 아주 간단하다. 우리는 SSA 형태의 개념, 간단한 SSA IR, 그것에 대한 성질 증명, 그리고 그 위에서 동작하는 몇 가지 최적화를 함께 만들어 볼 것이다.
제가 예전에 현대 SSA 컴파일러의 원조 격인 LLVM에 관해 글을 쓴 적이 있습니다. 이 글은 LLVM이 아니라, 일반적인 SSA에 관한 글입니다. 다만 그 글을 먼저 읽으면, 여기에서 다루는 내용 중 일부가 더 구체적으로 느껴질 수는 있습니다.
SSA는 중간 표현(IR)의 한 성질이며, 주로 _레지스터 머신_을 대상으로 하는 명령형 코드를 최적화하는 컴파일러에서 쓰인다. 레지스터 머신은 명령의 피연산자로 사용할 수 있는 고정된 집합의 _레지스터_를 제공하는 컴퓨터를 말한다. 이는 CPU, GPU, DSP 같은 특이한 것들을 포함해 사실상 모든 물리적 프로세서를 포괄한다.
SSA는 대개 컴파일러의 _미들엔드_에서 사용된다. 미들엔드는 _프런트엔드_와 백엔드 사이에 있으며, 프런트엔드는 프로그래머가 작성하는 _표면 언어_를 다루어 미들엔드 IR로 내리고, 백엔드는 최적화된 IR을 타깃 플랫폼의 어셈블리로 내린다.
그런데 SSA IR은 종종, 자신이 내려온 표면 언어와, 자신이 대상으로 삼는 어셈블리 언어와 닮지 않았다. 이는 두 표현 모두 컴파일러가 최적화 기회를 직관적으로 포착하기에 좋은 형태가 아니기 때문이다.
명령형 코드는 실행 중인 머신의 상태를 변경하는 연산들의 순서로 구성되며, 원하는 결과를 만들어낸다. 예를 들어 다음 C 프로그램을 보자:
int main(int argc, char** argv) {
int a = argc;
int b = a + 1;
a = b + 2;
b += 2;
a -= b;
return a;
}
이 프로그램은 입력과 무관하게 항상 0을 반환하므로, 다음처럼 최적화할 수 있다:
int main(int argc, char** argv) {
return 0;
}
하지만, 모든 연산이 서로 상쇄된다는 것을 일반적으로 판별하는 알고리즘을 어떻게 쓸까? 필요한 데이터 흐름 분석을 수행하려면 _프로그램 순서_를 머릿속에 계속 유지한 채, 프로그램 전체에 걸친 a와 b의 변화를 추적해야 한다. 그런데 이는 일반적이지 않고, 모든 경로를 따라가다 보면 큰 함수에 대해서는 탐색 공간이 매우 커진다. 대신, a와 b를 “가장 최근 값”을 계산하는 식으로 점진적으로 치환해 가는 방식으로 프로그램을 다시 쓰고 싶을 것이다:
int main(int argc, char** argv) {
int a = argc;
int b = a + 1;
int a2 = b + 2;
int b2 = b + 2;
int a3 = a2 - b2;
return a3;
}
그 다음에는 각 변수의 출현을 재귀적으로 그 우변 식으로 대체하고…
int main(int argc, char** argv) {
int a = argc;
int b = argc + 1;
int a2 = argc + 1 + 2;
int b2 = argc + 1 + 2;
int a3 = (argc + 1 + 2) - (argc + 1 + 2);
return (argc + 1 + 2) - (argc + 1 + 2);
}
상수들을 접어 합치고…
int main(int argc, char** argv) {
int a = argc;
int b = argc + 1;
int a2 = argc + 3;
int b2 = argc + 3;
int a3 = argc - argc
return argc - argc
}
마지막으로, 반환 값이 argc - argc라는 걸 보게 되고, 이를 0으로 바꿀 수 있다. 이제 다른 모든 변수는 쓰이지 않으므로 지울 수 있다.
이 방식이 잘 통하는 이유는, 변경이 있는 함수를 조합 회로(combinational circuit)로 바꾸었기 때문이다. 이는 상태가 없는 일종의 디지털 논리 회로로, 분석이 매우 쉽다. 회로의 노드(덧셈, 곱셈 같은 원시 연산에 해당)의 사이의 의존성은 구조만 보면 명확하다. 예를 들어, 1비트 곱셈기의 다음 회로도를 보자:
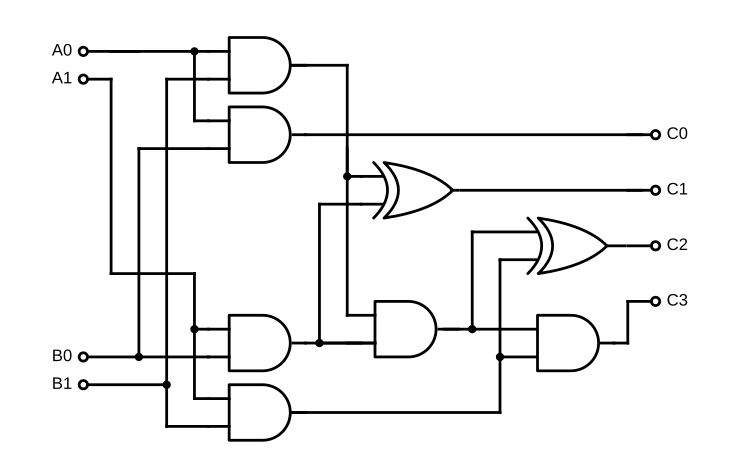
2진 곱셈기 (위키백과)
이런 그래프 형태로 표현된 연산 프로그램은 두 가지 큰 장점이 있다:
조합 회로가 최고의 회로인 이유는 그것이 유향 비순환 그래프(DAG)이기 때문이다. DAG는 아주 좋은 알고리즘을 허용한다. 예를 들어, 그래프에서의 최장 경로 문제는 NP-난해하다. 그러나 그래프가 DAG이면 O(n) 해법이 존재한다!
이 이점을 이해하기 위해, 다음 프로그램을 다시 보자:
int f(int x) {
int y = x * 2;
x *= y;
const int z = y;
y *= y;
return x + z;
}
이전처럼 각 변수를 그 정의로 치환하고 싶다고 해 보자. 그러나 단지 상수 변수라고 해서 그것을 정의한 식으로 치환할 수는 없다. 그러면 다른 프로그램이 되기 때문이다!
int f(int x) {
int y = x * 2;
x *= y;
// const int z = y; // z를 그 정의로 대체.
y *= y;
return x + y;
}
이제 제곱 연산이 더 이상 미사용이 아니게 되어, y 항이 하나 더 생겼다! 회로 형태로 바꿀 수는 있지만, 그러려면 모든 변경마다 새로운 변수를 끼워 넣어야 한다.
하지만 복잡한 제어 흐름이 끼어들면 이렇게 할 수 없다! 따라서 우리의 모든 알고리즘은 변경과 프로그램 순서를 꼼꼼히 고려해야 하고, 그 결과로 멋진 그래프 알고리즘을 별도 수정을 거치지 않고는 사용할 수 없게 된다.
SSA는 “정적 단일 할당”(static single assignment)의 약자로, 80년대에 개발되었다. 당시 널리 쓰이던 3-주소 코드(모든 문장이 x = y op z 꼴인 표현)를 확장하여, 위에서 설명한 것과 매우 비슷한 절차로 모든 프로그램을 회로처럼 만들고자 했다.
SSA 불변식은, 프로그램의 모든 변수는 정확히 하나의 연산에 의해 할당된다는 것이다. 프로그램의 모든 연산을 한 번씩 방문하면, 그것들은 하나의 조합 회로를 이룬다. 모든 변환은 이 불변식을 존중해야 한다. 회로 관점에서, 프로그램은 연산이 노드가 되고 “레지스터”(SSA에서 변수를 흔히 이렇게 부른다)가 엣지가 되는 그래프이다(정확히는, 각 연산의 출력이 레지스터에 대응한다).
하지만 다시, 제어 흐름 문제가 있다. 루프를 회로화할 수 있을까? SSA의 핵심 관찰은, 프로그램의 _대부분_은 회로에 가깝다는 점이다. 기본 블록(basic block)은 프로그램의 최대 회로적 성분이다. 간단히 말하면, 비-제어 흐름 연산의 연속과, 제어를 다른 기본 블록으로 넘기는 마지막 터미네이터 연산으로 이뤄진다.
기본 블록들 자체가 그래프를 이루는데, 이를 제어 흐름 그래프(control flow graph), 줄여서 CFG라 한다. 이런 정식화의 SSA는 때때로 SSA-CFG9라고도 불린다. 이 그래프는 일반적으로 DAG가 아니다. 하지만 프로그램을 기본 블록으로 분리하면, “비-DAG”적인 부분을 깔끔히 분리해 낼 수 있어, 기본 블록 내부에서는 더 단순한 분석을 할 수 있다.
SSA-CFG에는 동치인 두 가지 형식주의가 있다. 전통적 방식은 특수한 “phi” 연산(흔히 _phi 노드_라 부르며, 여기서도 그렇게 부르겠다)을 사용해, 기본 블록 사이의 레지스터를 연결한다. LLVM이 쓰는 방식이다. 더 현대적인 접근법은 MLIR이 사용하는 블록 인자(block arguments)다. 각 기본 블록이 함수처럼 매개변수를 명시하고, 그 블록으로 제어를 넘기는 쪽이 해당 타입의 인자를 넘겨야 한다.
코드를 좀 보자. 먼저, 루프로 피보나치 수를 계산하는 다음 C 함수를 생각해 보자.
int fib(int n) {
int a = 0, b = 1;
for (; n > 0; --n) {
int c = a + b;
a = b, b = c;
}
return a;
}
이를 SSA-CFG IR로 어떻게 표현할까? 이제 우리의 SSA IR을 발명해 보자! 제가 익숙한 LLVM IR과 조금 닮을 것이다.
// 전역(함수 포함)은 $로, 레지스터는 %로 시작한다.
// 각 함수는 시그니처를 선언한다.
func fib(%n: i32) -> (i32) {
// 첫 블록은 라벨이 없고 "점프"할 수 없다.
//
// 단일 인자 goto는 인자를 주고 해당 블록으로 곧장 점프한다.
goto @loop.start(%n, 0, 1)
// 블록 라벨은 !로 시작하고, 점을 포함할 수 있으며,
// 매개변수를 정의한다. 레지스터 이름의 유효 범위는 블록이다.
@loop.start(%n, %a, %b: i32):
// 정수 비교: %n > 0
%cont = cmp.gt %n, 0
// 다중 인자 goto는 스위치문과 같다. 컴파일러는
// `%cont`가 goto에 나열된 경우들 중 하나라고 가정할 수 있다.
goto %cont {
0 -> @ret(%a), // Goto는 함수 종료로 점프할 수 있다.
1 -> @loop.body(%n, %a, %b),
}
@loop.body(%n, %a, %b: i32):
// 덧셈과 뺄셈.
%c = add %a, %b
%n.2 = sub %n, 1
// @loop.start에서의 대입을 주목:
// %n = %n.2, %a = %b, %b = %c
goto @loop.start(%n.2, %b, %c)
}
모든 블록은 goto로 끝나며, 그 과정에서 하나 이상의 블록으로 제어를 넘긴다. 이때 그 블록을 인자들과 함께 “호출”한다. 기본 블록을, 같은 함수 내 다른 기본 블록으로 테일10 호출하는 아주 작은 함수로 생각하면 된다.
LLVM IR은… 좀 오래되었고, 따라서 옛 형식주의인 phi 노드를 쓴다. “Phi”는 “phony”에서 왔는데, 동작상 아무 일도 하지 않는 연산이기 때문이다. 선행자에서 넘어온 레지스터를 서로 연결만 해 준다.
phi연산은 사실상 선행자에 대한 switch-case다. 각 case는 그 선행자에서 온 레지스터(또는 즉시값)를 선택한다. 예컨대@loop.start에는 두 선행자가 있다. 함수 진입의 암묵적 블록인@entry, 그리고@loop.body다. phi 노드 IR에서는,%n용 블록 인자를 두는 대신 다음처럼 지정한다.
%n = phi { @entry -> 0, @loop.body -> %n.2 }
phi연산의 값은, 이 블록으로 점프해 온 선행자에서 넘어온 그 값이 된다.손으로 쓰거나 읽을 때는 조금 불편하지만, 알고리즘을 묘사할 때(“phi 노드를 추가해라”라고만 하면 되므로)나 메모리 상의 표현에서는 더 편리하다. 기능적으로는 완전히 동등하다.
C에서 우리 IR로의 변환을 이해하기 더 쉽도록, 먼저 C 코드를 for 루프 대신 goto를 쓰도록 고쳐 보자:
int fib(int n) {
int a = 0, b = 1;
start:
if (n > 0) goto ret;
int c = a + b;
a = b, b = c;
goto start
ret:
return a;
}
하지만 여전히 변경이 존재하므로, 이는 SSA가 아니다. SSA로 들어가려면, 모든 대입을 새로운 레지스터로 바꾸고, 어떻게든 블록 인자를 끼워 넣어야 한다…
위의 IR 코드는 이미 부분적으로 최적화되어 있다. C 프로그램의 이름 붙은 변수들이 메모리에서 끌어 올려져(lifted) 레지스터가 되었다. C 프로그램의 각 이름 붙은 변수를 포인터로 표현하면, 곧장 SSA 형태로 들어갈 필요 없이 이를 피할 수 있다. 이 기법은 Clang처럼 LLVM으로 내리는 프런트엔드들이 사용한다.
우리 IR을 확장해, 함수에 stack 선언을 추가해 보자. 이는 함수가 사용할 스택의 임시 공간을 정의한다. 각 스택 슬롯은 포인터를 만들어 내고, 그 포인터로 load와 store를 수행할 수 있다.
피보나치 함수는 이제 다음처럼 보일 것이다:
func &fib(%n: i32) -> (i32) {
// 스택 슬롯을 선언한다.
%np = stack i32
%ap = stack i32
%bp = stack i32
// 초기값을 적재한다.
store %np, %n
store %ap, 0
store %bp, 1
// 루프 시작.
goto @loop.start(%np, %ap, %bp)
@loop.start(%np, %ap, %bp: ptr):
%n = load %np
%cont = cmp.gt %n, 0
goto %cont {
0 -> @exit(%ap)
1 -> @loop.body(%n, %a, %b),
}
@loop.body(%np, %ap, %bp: ptr):
%a = load %ap
%b = load %bp
%c = add %a, %b
store %ap, %b
store %bp, %c
%n = load %np
%n.2 = sub %n, 1
store %np, %n.2
goto @loop.start(%np, %ap, %bp)
@exit(%ap: ptr):
%a = load %ap
goto @ret(%ap)
}
이름 붙은 변수를 참조할 때마다, 해당 스택 슬롯에서 로드하고, 대입할 때마다 그 슬롯에 스토어한다. C에서 이 형태로 내리기는 매우 쉽지만, 포인터 연산이 쓸데없이 많아 코드가 별로다. 어떻게 이걸 앞서 보여 준 레지스터 전용 함수로 바꿀 수 있을까?
재배치를 위해서 프로그램 순서가 중요하지 않기를 원하지만, 지금처럼 코드를 쓰면 프로그램 순서가 _중요_해진다. 로드는 이전 스토어에 의존하지만, 스토어는 그 둘을 연결할 수 있는 값을 생산하지 않는다.
“주소 공간”을 나타내는 피연산자를 도입하면, 순서 비의존성을 되찾을 수 있다. 로드/스토어는 주소 공간을 인자로 받고, 스토어는 새로운 주소 공간을 반환한다. 주소 공간(
mem)은 메모리의 어떤 영역의 상태를 나타낸다. 로드와 스토어는mem인자로 연결되지 않으면 서로 독립이다.이런 강화는 예를 들어 Go의 SSA IR이 사용한다. 다만 예시를 복잡하게 하므로, 여기서는 손을 휘저으며 넘어가겠다.
이제 최적화 패스의 정의와 정당성에 중요한, CFG에 대한 몇 가지 성질을 증명해야 한다.
먼저 몇 가지 정의부터.
기본 블록의 선행자(predecessors, “preds”)는, 해당 블록 으로 나가는 간선을 가진 블록들의 집합이다. 블록 자신이 자신의 선행자일 수도 있다.
일부 문헌은 위를 “직접” 또는 즉시 선행자라 부른다. 예를 들어, 우리의 예시에서 @loop.start의 선행자는 @entry(함수 진입점의 특수 이름)와 @loop.body다.
기본 블록의 후속자(successors, 줄여도 "succs"는 아님)는, 해당 블록 에서 나가는 간선을 가진 블록들의 집합이다. 블록 자신이 자신의 후속자일 수도 있다.
@loop.start의 후속자는 @exit와 @loop.body다. 후속자는 루프의 goto에 나열되어 있다.
블록 @a가 블록 @b의 추이적 선행자라면, @a가 @b를 약하게 지배(weakly dominate)한다고 하거나, @a가 @b의 _약한 지배자_라고 한다. 예를 들어, @entry, @loop.start, @loop.body는 모두 @exit을 약하게 지배한다.
하지만 이는 보통 그다지 유용한 관계가 아니다. 대신, 지배(dominators)를 말하고자 한다:
블록
@a는 지배자(dominates)@b이다, 라고 말하려면,@b의 모든 선행자가@a에 의해 지배되거나,@a가@b자신이어야 한다.동치로,
@b의 지배자 집합은 그 선행자들의 지배자 집합의 교집합에@b를 더한 것이다.
지배 관계에는 SSA의 핵심 그래프 알고리즘을 정의하는 데 필요한 좋은 순서 성질이 있다.
우리는 @entry에서 도달 가능한 모든 블록으로 이뤄진, 즉 @entry가 선행자가 없는 루트인 흐름 그래프(flowgraph)인 CFG만을 고려한다. 이는 증명에서 병적인 그래프를 제거하기 위해 필요하다. 중요하게도, 어떤 블록 @b에 대해서도, @entry에서 @b로 가는 사이클 없는 경로11을 항상 요구할 수 있다.
지배 관계를 동치로 표현하는 다른 방법은, @entry에서 @b로 가는 모든 경로가 @b의 모든 지배자를 포함한다는 것이다.
@a가@b를 지배한다는 것과,@entry에서@b로 가는 모든 경로가@a를 포함한다는 것은 동치다.먼저,
@entry에서@b로 가는 모든 경로가@a를 포함한다고 하자.@b가@a이면 끝. 아니면@b의 각 선행자가@a에 의해 지배됨을 보여야 한다. 이는@entry에서@b로 가는 사이클 없는 경로의 길이에 대한 귀납으로 보일 수 있다.@b의 선행자@p들 중@a가 아닌 것들을 보자.@entry에서@p로 가는 모든 사이클 없는 경로 p를 생각하면, 끝에@b를 덧붙인 경로 p'는@entry에서@b로 가는 사이클 없는 경로이며, 따라서@a를 포함한다. 마지막과 끝에서 두 번째 원소가 모두@a가 아니므로,@a는 더 짧은 경로 p 안에 있어야 한다. 그러므로 귀납으로@a는@p를 지배하고, 따라서@b를 지배한다.반대로,
@a가@b를 지배한다고 하고,@entry에서@b로 가는 경로 p를 보자. p의 끝에서 두 번째 원소는@b의 선행자@p다. 그것이@a이면 끝. 아니면,@b를 끝에서 삭제한 경로 p'를 생각하자.@p는@a에 의해 지배되고, p'는 p보다 짧으므로, 위와 같이 귀납을 진행할 수 있다.
좋은 성질들로 넘어가자. 지배를 이용하면, 임의로 복잡한 CFG에서 블록들을 지배 순서대로 정렬한 DAG를 끌어낼 수 있다.
지배 관계는 부분 순서다.
지배는 정의상 반사적이고 추이적이다. 따라서 남은 것은 서로가 서로를 지배할 수 없음을 보이는 것이다.
서로 다른
@a,@b가 서로를 지배한다고 하자.@entry에서@a로 가는 사이클 없는 경로 p를 고르자.@b가@a를 지배하므로, 이 경로의 접두사 중@b로 끝나는 것이 있다. 그런데@a가@b를 지배하므로, 그 접두사의 접두사 중@a로 끝나는 것이 있다. 이제 p에는@a가 두 번 등장하게 되어, 사이클 없다는 가정과 모순이다.
이제 @a < @b는 @a가 @b를 지배함을 뜻하도록 쓰자. 부분 순서 정리로부터 곧바로 따르는, 더 정제된 그래프 구조가 있다.
기본 블록의 지배자들은 지배 관계에 의해 전순서로 정렬된다.
@a1 < @b이고@a2 < @b인데, 서로가 서로를 지배하지 않는다고 하자. 그러면@entry에서@b로 가는 사이클 없는 경로가 둘 있으며, 두 경로는@a1과@a2를 포함하지만 서로 다른 순서로 포함한다. 그 경로들에서,@entry ... @a1을 따르는 부분 경로와,@a1 ... @b를 따르는 부분 경로를 취하면, 둘 중 어느 것도@a2를 포함하지 않는다. 이 둘을 이어 붙이면@entry에서@b로 가는 경로가 되는데, 이는@a2를 포함하지 않으므로 모순이다.
이는 지배 관계로 얻는 DAG가 사실 @entry를 루트로 하는 트리임을 알려 준다. 이 트리에서 노드의 부모를 그 노드의 즉시 지배자(immediate dominator)라고 한다.
지배자 계산은 반복적으로 할 수 있다. 블록 @b의 지배자 집합은, @b의 선행자들의 지배자 집합의 교집합에 @b를 더한 것이다. 이 알고리즘은 이차 시간에 동작한다.
더 나은 알고리즘은 Lengauer-Tarjan 알고리즘[^lta]이다. 비교적 단순하지만, 여기에서 구현을 설명하는 것은 범위를 벗어난다. 좋은 정리를 여기에서 찾았다.
중요한 점은, 지배자 트리를 무리 없이 계산할 수 있고, 주어진 임의의 노드에 대해 그 즉시 지배자를 물을 수 있다는 것이다. 이제 즉시 지배자를 사용하여, 지배자의 마지막 중요한 성질을 도입하자.
블록
@a의 지배 경계(dominance frontier)는,@a가 지배하지는 않지만, 선행자 중 적어도 하나는@a가 지배하는 모든 블록들의 집합이다.
이 점들은, 서로 다른 경로에서 제어 흐름이 합쳐지는 지점이다. 하나는 @a를 포함하고, 다른 하나는 포함하지 않는다. @loop.body의 지배 경계는 @loop.start인데, 그 선행자는 @entry와 @loop.body이다.
지배 경계를 계산하는 방법은 여럿 있지만, 지배 트리를 손에 넣었을 때는 다음처럼 할 수 있다:
각 블록
@b에 대해 선행자가 둘 이상이면, 각 선행자에 대해 그 선행자를@p라 하자.@b를@p와 그 모든 지배자의 지배 경계에 추가하되,@b의 즉시 지배자를 만나면 멈춘다.알고리즘이 검토한 모든 블록이 올바른 경계에 들어감을 보여야 한다.
먼저, 검토된 블록
@b가 올바른 경계에 추가되는지 확인한다.@p가@b의 선행자이고,@a < @p이며,@d가@b의 즉시 지배자라고 하자. 만약@a < @d이면,@a는@b를 지배하므로@b는@a의 경계에 있지 않다. 그렇지 않다면,@a는@b를 지배할 수 없고(그랬다면@a는@d에 의해 지배되었을 터이므로 모순),@a는 어떤 선행자를 지배하므로@b는@a의 경계에 있어야 한다.다음으로, 각 경계가 완전함을 확인한다. 블록
@a를 하나 잡자. 검토된 블록@b가 그 경계에 있다면,@a는 어떤 선행자@p의 지배자들 중 하나여야 하고, 동시에@b의 즉시 지배자에 의해 지배되어야 한다. 그렇지 않으면@a가@b를 지배하게 되어(따라서@b는 경계에 없음) 모순이다. 그러므로@b는@a의 지배자에 추가된다.
이 모든 알고리즘의 시간 복잡도가 이차라는 걸 눈치챘을 것이다. 사실, 컴파일러 관련 그래프 알고리즘에서 이는 매우 좋은 시간 복잡도다. 세제곱, 네제곱 알고리즘은 드물지 않으며, 그렇다, 여러분의 최적화 컴파일러의 시간 복잡도는 아마도 프로그램 크기에 대해 3차나 4차일 것이다!
좋다. 이제 최적화를 하나 구성하자. 어떤 포인터에 대한 로드를, 그 포인터로의 가장 최근 스토어로 대체할 수 있는지 알아내고 싶다. 이렇게 하면 스토어/로드 쌍을 상쇄시켜 값을 메모리에서 완전히 끌어 올릴 수 있다.
이를 위해 또 하나의 암묵적인 그래프 자료구조를 사용한다.
데이터플로 그래프는 각 기본 블록의 내부 회로 그래프들을, 블록 인자들을 따라 연결해 만든 유향 그래프다.
use-def 체인을 따라간다는 것은, 어떤 연산으로부터 이 그래프를 앞으로 따라가 그 연산에 잠재적으로 의존하는 연산을 찾거나, 뒤로 따라가 그 연산이 잠재적으로 의존하는 연산을 찾는 것을 말한다.
데이터플로 그래프는, CFG와 마찬가지로, 잘 정의된 “위쪽” 방향이 _없다_는 점을 기억하는 게 중요하다. 이것과 CFG를 탐색하려면 지배자 트리가 필요하다.
또 하나 기억할 점은, 기본 블록에서 그 블록이 실행되면 그 안의 모든 명령이 항상 실행된다는 것이다. 이 분석의 많은 부분에서, 블록 내 마지막 로드를 고르기 위해 “프로그램 순서”를 참조해야 하는데, 항상 그렇게 할 수 있다. 이는 최적화 구성에 기본 블록이 필수적인 중요한 성질이다.
주어진 store %p, %v에 대해, 여기에 의존하는 모든 로드를 식별하고 싶다. %p의 use-def 체인을 따라가면, 그 스토어(이를 %s라 하자)에 잠재적으로 의존하는 로드가 들어 있는 블록들을 찾을 수 있다.
먼저, 같은 기본 블록(이를 @a라 하자) 안의 로드를 제거할 수 있다. 프로그램 순서 기준으로, s 이후(하지만 다른 store %p, _ 이전)의 모든 load %p를 %v의 정의로 바꾼다. 만약 s가 이 블록의 마지막 스토어가 아니라면, 여기서 끝이다.
그렇지 않다면, %p의 use-def 체인을 따라가 %p를 사용하는 후속자, 즉 goto의 case 인자 중 %p가 하나라도 있는 후속자들로 간다. 이러한 후속자들로 재귀하며, 이때 관심 있는 포인터 %p를 해당 후속자에서 %p로 설정된 블록 매개변수들로 대체한다(두 개 이상이 %p일 수도 있다).
후속자 @b가 %p를 담고 있는 레지스터 중 하나에서 로드한다면, %p에 대한 스토어 전에 있는 모든 그런 로드를 바꿔 준다. 이제 %v를 어떻게든 @b로 전달해야 한다.
여기에서 문제가 하나 생긴다. @b의 선행자가 정확히 하나라면, 그 레지스터(귀납적으로 존재하는) 중 %v를 들고 있는 것을 전달하기 위해 새로운 블록 인자를 추가해야 한다. 이미 다른 인자로 %v가 @b로 전달되고 있다면, 그 인자를 그대로 쓰면 된다.
하지만 @b의 선행자가 여러 개라면, @a에서 @b로 가는 모든 경로가 %v를 보내도록 만들어야 하고, 이것들을 표준화하는 일이 까다롭다. 더 나쁜 건, @b가 @a의 지배 경계에 있다면, 다른 스토어가 그 로드에 기여하고 있을 수도 있다는 점이다! 이런 이유로, 스토어에서 로드로의 데이터플로는 좋은 전략이 아니다.
대신, 로드에서 스토어로 거꾸로 데이터플로를 보자(일반적으로, use에서 def로의 데이터플로가 더 유용한 경향이 있다). 이렇게 하면 위의 순방향 분석을 보강해, 지배 경계 주변의 복잡한 문제를 제거할 수 있다.
이번에는 로드를 분석하자. 각 @a 안의 load %p에 대해, 그 값에 잠재적으로 기여할 수 있는 모든 스토어를 결정하고 싶다. 다음과 같이 그 스토어들을 찾을 수 있다:
주어진 블록에서 %p의 값을 담는 레지스터가 무엇인지 결정하고, 그 블록 안에서의 마지막 스토어를 찾고자 한다.
이를 위해 CFG를 BFS 순서로 뒤로 범람 탐색(flood-fill)한다. 즉, 선행자(를 use-def 체인을 통해) 재귀적으로 따라가되, 각 선행자를 그들의 선행자보다 먼저 방문하고, 기본 블록은 다시 방문하지 않는다(다만 마지막에 @a는 되돌아올 수도 있다).
@b에서 %p의 “동치”12 %p.b를 결정하는 일은 재귀적으로 할 수 있다. @b를 검사하면서 %p.b의 정의를 따라가자. %p.b가 블록 매개변수라면, 각 선행자 @c에 대해, @c의 goto 안 @b(...) case에서 해당 인자를 %p.c로 둔다.
이 정보를 사용해, 해당 로드가 잠재적으로 의존하는 모든 스토어를 수집할 수 있다. 만약 선행자 @b가 %p.b로 스토어를 한다면, 그 블록에서의(프로그램 순서상) 마지막 스토어를 집합에 추가하고, @b의 선행자들로는 재귀하지 않는다(이 스토어가 과거의 모든 스토어를 덮어쓰기 때문이다). 이 과정에서 @a로 다시 돌아와, 그 블록 내 %p에 대한 스토어를 수집할 수도 있다. 루프의 경우에는 이것이 필요하다.
결과는 (store %p.s %v.s, @s) 쌍들의 집합 stores가 된다. 이 과정에서 방문한 모든 블록들의 집합 subgraph도 수집했는데, 이는 @a의 지배자들이며, %v.b를 통해 흘려야 한다. 이 과정을 _메모리 의존성 분석_이라 부르며, 많은 최적화들의 핵심 구성 요소다.
모든 기여 연산이 스토어인 것은 아니다. 전역 참조(여기서는 무시)일 수도 있고, 함수 인자나 함수 호출의 결과일 수도 있다(이 경우에는 아마도 로드를 올릴 수 없다). 예컨대
%p가 함수 인자까지 추적된다면, 우리가 볼 수 없는 스토어만 있는 포인터에서 로드하는 코드 경로가 있다는 뜻이다.
또한 스토어되지 않을 수도 있는 스택 슬롯으로 거슬러 올라갈 수도 있다. 이는 초기화되지 않은 메모리를 로드할 수 있는 코드 경로가 있음을 뜻한다. LLVM처럼, 이는 관찰 가능한 동작이 아니라고 가정할 수 있으므로, 그런 의존성은 배제한다. 모든 의존성이 초기화되지 않은 로드뿐이라면, 해당 로드뿐 아니라 그에 의존하는 연산들까지(역방향 데이터플로 분석이 이른바 “시간여행” UB의 근원이다) 잠재적으로 지울 수 있다.
이제 전체 의존성 정보를 얻었으니, 로드를 올리기 시작할 수 있다. 로드의 모든 의존성이 현재 함수의 스토어이거나, 표면 언어의 UB 덕에 무시할 수 있는 의존성(null 로드나 초기화되지 않은 로드 등)이라면, 안전하게 올릴 수 있다.
이 알고리즘에는 블록 인자를 통한 값 “배관(plumbing)”이 많이 등장한다. 많은 IR은 단순화를 위해, 각 블록이 묵시적으로 지배자로부터 넘어오는 레지스터들을 블록 인자로 받는 것으로 취급한다.
여기서는 무슨 일이 벌어지는지 더 뚜렷이 보이도록, 이 “배관”을 명시적으로 유지하겠다. 다만 실제로는, 지배 경계에서만 특별히 신경 쓰면 되고, 나머지는 대부분 백그라운드에서 처리된다.
어떤 로드를 안전하게 올릴 수 있다고 하자. 이제 저장된 값을 그 로드까지 배관해야 한다. 각 블록 @b에 대해 subgraph 안에서(별도로 언급하지 않는 한 다른 모든 블록도 이제 subgraph 안에 있게 된다) 다음을 수행한다. 두 매핑을 구성할 것이다. 하나는 (@s, @b) -> %v.s.b로, %v.s의 해당 블록에서의 동치 레지스터다. 다른 하나는 @b -> %v.b로, 해당 블록에서 %p가 가져야 하는 값이다.
@s를 초기 원소로 넣는다.@a를 큐에서 하나 꺼낸다. 각 후속자 @b(단, subgraph 안인 것)에 대해:
%v.b가 아직 정의되어 있지 않으면, 블록 인자로 하나 추가한다. @a가 그 인자에 %v.a를 전달하게 한다.@b가 아직 방문되지 않았고, 우리가 삭제하려는 로드가 들어 있는 블록이 아니라면, 큐에 추가한다.모두 끝나면, @a가 로드를 담고 있는 블록이라면, 이제 %p에 대한 모든 로드를 %p에 대한 어떤 스토어보다 앞서 있는 경우에 한해 %v.a로 대체할 수 있다.
이 전체 과정을 생략할 수 있는 경우가 있다. “피프홀” 최적화를 적용하는 것이다. 예를 들어, 같은 기본 블록에서 스토어 다음에 로드가 오는 경우는, 로컬하게 최적화해 없애고, 블록 사이의 스토어/로드 쌍에 대해서만 무거운 분석을 남겨 둘 수 있다.
피보나치 함수에 대해 의존성 분석을 수행한 결과다. 각 로드에는 stores 안의 블록과 스토어를 주석으로 달았다.
func &fib(%n: i32) -> (i32) {
%np = stack i32
%ap = stack i32
%bp = stack i32
store %np, %n // S1
store %ap, 0 // S2
store %bp, 1 // S3
goto @loop.start(%np, %ap, %bp)
@loop.start(%np, %ap, %bp: ptr):
// @entry: S1
// @loop.body: S6
%n = load %np // L1
%cont = cmp.gt %n, 0
goto %cont {
0 -> @exit(%ap)
1 -> @loop.body(%np, %ap, %bp),
}
@loop.body(%np, %ap, %bp: ptr):
// @entry: S1
// @loop.body: S4
%a = load %ap // L2
// @entry: S2
// @loop.body: S5
%b = load %bp // L3
%c = add %a, %b
store %ap, %b // S4
store %bp, %c // S5
// @entry: S1
// @loop.body: S6
%n = load %np // L3
%n.2 = sub %n, 1
store %np, %n.2 // S6
goto @loop.start(%np, %ap, %bp)
@exit(%ap: ptr):
// @entry: S2
// @loop.body: S5
%a = load %ap // L4
goto @ret(%ap)
}
L1을 보자. 기여하는 스토어는 @entry와 @loop.body에 있다. 그러니 새 매개변수 %n을 추가한다. @entry에서는 그 매개변수에 %n을(해당 블록에서 저장된 값), @loop.body에서는 %n.2를 넘긴다.
L4는 어떨까? 기여하는 스토어는 @entry와 @loop.body에도 있지만, 그중 하나는 @exit의 선행자가 아니다. 다만 이 로드의 subgraph에는 @loop.start도 있다. 그래서 @entry부터 시작해, @loop.body에 새 매개변수 %a를 추가하고, 0(저장된 값, 이번엔 즉시값)을 흘려 보낸다. 이제 @loop.body를 보면, 이 로드용 매개변수(%a)가 이미 있으므로, 그 인자로 %b를 넘기기만 하면 된다. 다음으로 @loop.start를 처리하는데, 이는 @entry가 큐에 넣어 둔 블록이다. @exit는 새 매개변수 %a를 받고, @loop.start의 %a를 거기로 흘려 보낸다. @loop.start의 goto에 @loop.body가 나타나더라도, 이미 방문했으므로 다시 처리하지 않는다.
다른 두 로드에 대해서도 이 작업을 하면, 다음을 얻는다:
func &fib(%n: i32) -> (i32) {
%np = stack i32
%ap = stack i32
%bp = stack i32
store %np, %n // S1
store %ap, 0 // S2
store %bp, 1 // S3
goto @loop.start(%np, %ap, %bp, %n, 0, 1)
@loop.start(%np, %ap, %bp: ptr, %n, %a, %b: i32):
// @entry: S1
// @loop.body: S6
// %n = load %np // L1
%cont = cmp.gt %n, 0
goto %cont {
0 -> @exit(%ap, %a)
1 -> @loop.body(%np, %ap, %bp, %n, %a, %b),
}
@loop.body(%np, %ap, %bp: ptr, %n, %a, %b: i32):
// @entry: S1
// @loop.body: S4
// %a = load %ap // L2
// @entry: S2
// @loop.body: S5
// %b = load %bp // L3
%c = add %a, %b
store %ap, %b // S4
store %bp, %c // S5
// @entry: S1
// @loop.body: S6
// %n = load %np // L3
%n.2 = sub %n, 1
store %np, %n.2 // S6
goto @loop.start(%np, %ap, %bp, %n.2, %b, %c)
@exit(%ap: ptr, %a: i32):
// @entry: S2
// @loop.body: S5
// %a = load %ap // L4
goto @ret(%a)
}
올린 뒤에, 어떤 스택 슬롯의 포인터가 이스케이프하지 않는다는 것을 안다면(즉, 그 포인터의 사용들 중 어떤 것도 함수 호출13로 들어가거나, 전역(또는 이스케이프하는 포인터) 쓰기로 들어가지 않는다면), 해당 포인터로의 모든 스토어를 지울 수 있다. 스택 슬롯에 대한 모든 스토어를 지우면, 그 스택 슬롯 자체도 지울 수 있다(이 시점에는 해당 슬롯에 대한 로드가 남아 있지 않아야 한다).
이 분석은, 일반적으로 포인터들이 서로 앨리어싱하지 않는다고 가정하기 때문에 단순하다. 더 정확한 의존성 분석을 위해서는 앨리어싱 분석이 필요하다. 예컨대 구조체의 하위 객체 포인터를 통한 필드 로드 올리기나, 일반적인 포인터 산술을 다루려면 그렇다.
하지만 우리의 의존성 분석은, 서로 다른 선행자에서 같은 블록으로 다른 포인터들이 인자로 전달되는 경우에도 _견고_하다. 바로 지배 경계를 둘러싼 모든 배관 작업이 처리해 주는 경우다. 이 견고함은 궁극적으로 SSA의 회로적 특성에서 온다.
비슷하게, select %cond, %a, %b(사실상 삼항) 같은 것을 다루려면 이 분석을 조금 손봐야 한다. 포인터에 대한 select는, 로드된 값에 대한 select로 바꿔야 하는데, 이는 올리기 변환을 “한꺼번에” 해야 함을 뜻한다. 올릴 수 있는 로드의 일부만 먼저 올려 버리면, 나머지를 다 올릴 때까지 IR이 불일치한 상태가 된다.
많은 최적화는 CFG를 엉망으로 만들므로, 변환이 남긴 찌꺼기를 “청소”하는 간단한 패스가 유용하다. 쉬운 예를 몇 가지 보자.
어떤 연산의 결과가 사용처가 0이고, 그 연산이 부작용이 없다면 지울 수 있다. 이렇게 하면, 그 연산에 의존하지만 이제 사용처가 없는 연산도 연쇄적으로 지울 수 있다. SSA의 회로적 특성 덕분에 이 작업은 매우 단순하다. 출력 사용처가 0인 명령들을 모아 지운다. 그런 다음, 그 피연산자들의 정의를 살핀다. 그 연산들도 이제 사용처가 0이 되었다면 지우고, 재귀한다.
이는 블록 인자까지 거슬러 올라간다. 블록 인자를 지우는 일은 약간 까다롭지만, 작업 큐를 쓰면 된다. 모든 블록을 작업 큐에 넣는다.
중복된 CFG 구성은 여럿이며, 기본 블록의 수를 줄이기 위해 단순화할 수 있다.
예를 들어, 도달 불가능 코드가 블록 삭제를 돕는다. 다른 최적화로 인해 함수 끝의 goto가 비어(모든 후속자가 최적화되어 사라졌기 때문에) 버릴 수 있다. 빈 goto는(케이스가 없으므로!) 도달 불가능으로 취급하므로, 마지막 비순수 연산까지 블록의 모든 연산을 지울 수 있다. 블록의 모든 명령을 지웠다면, 블록 자체도 완전히 지우고, 선행자들의 goto에서도 지울 수 있다. 이는 일종의 죽은 코드 제거(DCE)로, 앞선 최적화와 결합하면 중복 코드를 대대적으로 삭제한다.
중복 점프도 있다. 예컨대, 어떤 블록의 선행자와 후속자가 정확히 하나씩뿐이라면, 선행자의 goto에서 그 블록을 가리키는 case를 곧장 후속자로 연결할 수 있다. 비슷하게, 두 블록이 서로의 유일한 선행자/후속자라면, 둘을 융합(fuse)할 수 있다. 즉, goto를 거치지 않고, 두 입력 블록의 회로를 직접 이어 붙여 하나의 블록을 만든다.
삼항 select 연산이 있으면 더 정교한 융합도 가능하다. 어떤 블록의 후속자가 둘이고, 그 둘의 유일한 후속자가 같은 블록이며, 그 후속자들이 goto만으로 이루어졌다면, 네 블록을 모두 융합해, CFG의 다이아몬드를 하나의 select로 바꿀 수 있다. C로 쓰면 다음 변환이다:
// Before.
int x;
if (cond) {
x = a;
} else {
x = 0;
}
// After.
int x = cond ? a : 0;
LLVM의 CFG 단순화 패스는 매우 정교하며, 복잡한 형태의 제어 흐름도 제거할 수 있다.
SSA 최적화 패스에 관해 더 쓰고 싶다. 이 주제는 매우 풍부하고, 최적화를 개별적으로 바라보는 것은, 단순하고 멍청한 구성 요소들로 정교한 최적화 파이프라인이 어떻게 만들어지는지 이해하는 훌륭한 방법이다.
그래프 이론의 실용적 적용 예이기도 하며, 그것이 얼마나 강력한지 보여 준다. (적어도 제 생각에는) 그래프 이론은 종종 매우 추상적으로 느껴지는데, SSA는 이를 이해하기에 직관적인 무대다.
앞으로는 CSE/GVN, 루프 최적화, 그리고 용기가 난다면 SSA를 벗어나 유한 레지스터 머신으로 내려가는 일(백엔드는 제 특기가 아니다!)도 다뤄 보고 싶다.
구체적으로는 LLVM IR로 내리기 전의 Swift 프런트엔드.↩
마이크로소프트가 판매하는, C++ 규격을 완전히 준수하지 않는 Microsoft Visual C++.↩
HotSpot은 OpenJDK가 제공하는 JVM 구현이다. C2는 “두 번째 컴파일러”로, HotSpot의 자바 실행 엔진 중 최고 성능을 낸다.↩
V8은 크로뮴의 자바스크립트 런타임이다.↩
SpiderMonkey는 파이어폭스의 자바스크립트 런타임이다.↩
안드로이드 플랫폼의 “JVM”(따옴표)의 역할을 하는 Android Runtime(ART).↩
글래스고 Haskell 컴파일러(GHC)는 SSA를 쓰지 않는다. (다른 일부 순수 함수형 언어들처럼) 연속성 지향 IR을 사용한다(Scheme의 call/cc를 떠올려 보자).↩
모든 컴파일러 사람들은 P≠NP를 굳게 믿는다. 프로그램 최적화에는 NP-난해 문제가 수두룩하고, 만약 다항 시간의 이상적인 레지스터 할당이 존재했다면 우리는 벌써 찾았을 테니까.↩
좀 더 최근 IR들은 “구조적 제어 흐름”(structured control flow, SCF)이라 불리는 SSA의 다른 버전을 쓴다. Wasm이 대표적인 SCF IR이다. SSA-SCF는 SSA-CFG와 동등하며, 둘 사이를 무손실로 변환하는 다항 시간 알고리즘이 존재한다(예컨대 Wasm을 LLVM으로 컴파일할 때는 “relooping algorithm”으로 CFG를 SCF로 바꾼다).
SCF에서는, switch문이나 루프 같은 연산을 기본 블록을 _포함하는_ 매크로 연산으로 표현한다. 예컨대, `switch` 연산은 값을 입력으로 받아 그것에 따라 실행할 기본 블록을 고르고, 그 기본 블록이 계산한 값을 자신의 출력으로 반환할 수 있다.
[RVSDG](https://arxiv.org/abs/1912.05036)는 이 영역의 주목할 만한 혁신으로, 전체 명령형 프로그램의 회로 분석을 가능하게 한다.
여기서는 SSA-CFG를 다룬다. 그쪽이 더 흔하고, LLVM IR이 그렇게 되어 있기 때문이다.
둘 사이 변환에 대한 내용은 이 [MLIR 발표 자료](https://llvm.org/devmtg/2024-04/slides/TechnicalTalks/Bock-LiftingCFGs.pdf)도 참고.[↩](https://mcyoung.xyz/2025/10/21/ssa-1/#fnref:non-cfg)
10. 테일 호출은, 어떤 함수 호출이 함수의 마지막 연산일 때를 말한다. 이 경우 호출자는 피호출자로 곧장 점프해, 자신의 스택 프레임을 재활용할 수 있다. 피호출자가 별도 스택 프레임을 할당할 필요가 없다.↩
@a에서 @b로 가는 임의의 경로가 주어지면, @c에서 @c로 가는 각 부분 경로를 단일 @c 노드로 바꿔, 사이클 없게 만들 수 있다.↩
어떤 기본 블록에서 선행자로 이동할 때, 그 블록에서 블록 매개변수로 정의된 레지스터는 각 선행자 안에서 어떤 레지스터(또는 즉시값)에 대응한다. 그것이 %p의 “동치”다.
“동치”가 즉시값일 수도 있다. 예를 들어 `null`이나 전역의 주소 `&g`가 그렇다. `&g`의 경우 자료 경합이 없다고 가정하면, 현재 함수 안의 이 전역에 대한 스토어가 (a) 존재하는지, (b) 올릴 수 있는지 알려면 별칭 정보가 필요하다.
동치가 `null`이라면, 최적화 수준에 따라 둘 중 하나로 진행할 수 있다. 만약 `null` 로드가 트랩을 일으켜야 한다(Go처럼)면, 이 로드는 올릴 수 없는 것으로 표시해야 한다. 트랩이 일어날 수 있기 때문이다. 만약 `null` 로드가 UB여야 한다면, 그 선행자를 그냥 무시한다. (우리 분석에서는) 포인터가 `null`이라면 결코 로드되지 않는다고 가정할 수 있기 때문이다.[↩](https://mcyoung.xyz/2025/10/21/ssa-1/#fnref:equiv-reg)
13. 반환된 스택 포인터는 이스케이프하지 않는다. 스택 슬롯의 수명은 함수 종료에서 끝나므로, 우리는 댕글링 포인터를 반환하게 되고, 그 포인터에서 로드가 일어나지 않는다고 가정한다. 따라서 그것을 반환하기 전에 그 포인터로의 스토어는 버릴 수 있다.↩