정규식 매칭에 대한 두 가지 접근(백트래킹 vs Thompson NFA)을 비교하고, Thompson 알고리즘을 이용해 간단하고 빠른 구현을 만드는 방법과 실제 세계의 정규식 기능을 다룬다.
URL: https://swtch.com/~rsc/regexp/regexp1.html
정규식 매칭은 단순하고 빠를 수 있다
(하지만 Java, Perl, PHP, Python, Ruby, ...에서는 느리다)
2007년 1월
이 글은 정규식 매칭에 대한 두 가지 접근법의 이야기다. 하나는 Perl을 포함해 많은 언어의 표준 인터프리터에서 널리 쓰인다. 다른 하나는 소수의 곳에서만 쓰이는데, 대표적으로 awk와 grep의 대부분 구현이 그렇다. 두 접근법은 성능 특성이 극단적으로 다르다.
문자열 반복을 나타내기 위해 위첨자 표기를 쓰자. 즉 a?3a3는 a?a?a?aaa의 줄임말이다. 두 그래프는 정규식 a?nan 를 문자열 an 에 대해 매칭하는 데 필요한 시간을 각 접근법별로 그린 것이다.
Perl은 29자짜리 문자열을 매칭하는 데 60초가 넘게 걸린다. 반면 나중에 설명할 이유로 Thompson NFA라고 표시된 다른 접근은 문자열을 매칭하는 데 20 마이크로초 가 걸린다. 오타가 아니다. Perl 그래프의 시간 단위는 초이고 Thompson NFA 그래프의 시간 단위는 마이크로초다. 즉, 29자라는 아주 작은 문자열에서조차 Thompson NFA 구현은 Perl보다 백만 배 빠르다. 그래프에서 보이는 추세는 계속된다. Thompson NFA는 100자 문자열을 200마이크로초도 안 되어 처리하는 반면 Perl은 10^15년이 넘게 걸릴 것이다. (Perl은 같은 알고리즘을 쓰는 수많은 인기 프로그램 가운데 가장 눈에 띄는 예일 뿐이다. 위 그래프는 Python, PHP, Ruby, 또는 다른 언어들일 수도 있다. 이 글의 뒤쪽에 다른 구현들의 데이터도 포함한 더 자세한 그래프가 나온다.)
그래프를 믿기 어려울 수도 있다. 아마 Perl을 써 봤고 정규식 매칭이 특별히 느리다고 느낀 적이 없을 것이다. 실제로 대부분의 경우 Perl의 정규식 매칭은 충분히 빠르다. 하지만 그래프가 보여주듯, Perl이 아주 아주 느리게 매칭하는 이른바 “병적(pathological)” 정규식을 작성하는 것은 가능하다. 반면 Thompson NFA 구현에는 병적인 정규식이 없다. 이 두 그래프를 나란히 보면 “그럼 왜 Perl은 Thompson NFA 방식을 쓰지 않을까?”라는 질문이 자연스럽다. 할 수 있고, 해야 하며, 이 글의 나머지는 그것에 관한 이야기다.
역사적으로 정규식은, 좋은 이론이 좋은 프로그램으로 이어진다는 컴퓨터 과학의 빛나는 사례 중 하나였다. 정규식은 원래 이론가들이 간단한 계산 모델로 개발했지만, Ken Thompson이 CTSS용 텍스트 편집기 QED 구현에서 이를 프로그래머 세계에 소개했다. Dennis Ritchie도 GE-TSS용 QED를 구현하며 이를 따랐다. Thompson과 Ritchie는 이후 Unix를 만들었고 정규식도 함께 가져왔다. 1970년대 후반에는 ed, sed, grep, egrep, awk, lex 같은 도구들에서 정규식이 Unix 환경의 핵심 기능이 되었다.
오늘날 정규식은 또한, 좋은 이론을 무시하면 나쁜 프로그램으로 이어진다는 빛나는 사례가 되었다. 오늘날 인기 있는 도구들이 사용하는 정규식 구현은 30년 전 Unix 도구들에 쓰이던 구현보다 상당히 느리다.
이 글은 좋은 이론을 되짚는다. 정규식, 유한 오토마타, 그리고 1960년대 중반 Ken Thompson이 발명한 정규식 검색 알고리즘을 다룬다. 또한 그 이론을 실제로 적용해 Thompson 알고리즘의 간단한 구현을 설명한다. C로 400줄도 안 되는 그 구현이 앞에서 Perl과 맞붙었다. 이 구현은 Perl, Python, PCRE 등에서 쓰는 더 복잡한 현실 세계 구현들을 능가한다. 글의 마지막에는 이 이론을 현실 세계 구현에 어떻게 적용할 수 있을지 논의한다.
정규식은 문자 문자열 집합을 기술하는 표기법이다. 특정 문자열이 어떤 정규식이 기술하는 집합에 속하면, 우리는 그 정규식이 그 문자열과 매칭된다(matches) 고 말한다.
가장 단순한 정규식은 하나의 리터럴 문자다. 특수 메타문자 *+?()| 를 제외하면 문자는 자기 자신과 매칭된다. 메타문자를 매칭하려면 백슬래시로 이스케이프한다. 예를 들어 \+ 는 리터럴 플러스 문자와 매칭된다.
두 정규식은 교대(alternation) 또는 연결(concatenation)하여 새로운 정규식을 만들 수 있다. _e_1이 _s_와 매칭되고 _e_2가 _t_와 매칭되면, _e_1|_e_2는 s 또는 _t_와 매칭되고, _e_1 _e_2는 _st_와 매칭된다.
메타문자 *, +, ? 는 반복 연산자다. _e_1* 는 _e_1과 매칭되는 문자열들(서로 달라도 됨)의 0개 이상 반복 시퀀스와 매칭된다. _e_1+ 는 1개 이상, _e_1? 는 0개 또는 1개와 매칭된다.
연산자 우선순위는 결합이 약한 것부터 강한 것까지, 먼저 교대, 그 다음 연결, 마지막으로 반복 연산자다. 산술식처럼 괄호로 의미를 강제할 수 있다. 예: ab|cd 는 (ab)|(cd) 와 같다. ab* 는 a(b*) 와 같다.
지금까지 설명한 문법은 전통적인 Unix egrep 정규식 문법의 부분집합이다. 이 부분집합만으로도 모든 정규 언어를 기술할 수 있다. 대략 말해 정규 언어는 텍스트를 한 번만 훑고 고정된 양의 메모리만으로 매칭할 수 있는 문자열 집합이다. 더 최신 정규식 기능(특히 Perl과 이를 베낀 것들)은 많은 새 연산자와 이스케이프 시퀀스를 추가했다. 이런 추가는 정규식을 더 간결하게 만들고 때로는 더 난해하게 만들지만, 보통 더 강력해지지는 않는다. 이런 화려한 새 정규식은 대부분 전통 문법으로 더 긴 동치 표현을 가질 수 있다.
추가적인 표현력을 실제로 제공하는 흔한 확장은 역참조(backreference) 다. \1 또는 \2 같은 역참조는 이전의 괄호로 둘러싼 표현식이 매칭한 문자열과 동일한 문자열에만 매칭된다. 예를 들어 (cat|dog)\1 은 catcat 과 dogdog 에 매칭되지만 catdog 나 dogcat 에는 매칭되지 않는다. 이론적으로 말해, 역참조가 있는 “정규식”은 정규식이 아니다. 역참조가 추가하는 힘은 대가가 크다. 최악의 경우, 가장 잘 알려진 구현도 Perl이 쓰는 것 같은 지수 시간 탐색 알고리즘이 필요하다. 물론 Perl(및 다른 언어들)이 지금 와서 역참조 지원을 제거할 수는 없지만, 역참조가 없는 정규식(앞에서 다룬 것들처럼)이 주어졌을 때는 훨씬 더 빠른 알고리즘을 사용할 수 있다. 이 글은 그 빠른 알고리즘에 관한 것이다.
문자열 집합을 기술하는 또 다른 방법은 유한 오토마타로 하는 것이다. 유한 오토마타는 상태 머신(state machine)이라고도 하며, 이 글에서는 “오토마타(automaton)”와 “머신(machine)”을 같은 의미로 쓴다.
간단한 예로, 정규식 a(bb)+a 가 매칭하는 문자열 집합을 인식하는 머신은 다음과 같다.

유한 오토마타는 항상 그 상태들 중 하나에 있으며, 그림에서는 원으로 표시된다. (원 안의 숫자는 설명을 돕기 위한 라벨로, 머신의 동작 자체에는 포함되지 않는다.) 문자열을 읽으면서 상태에서 상태로 전이한다. 이 머신에는 두 개의 특별한 상태가 있다. 시작 상태 _s_0과 매칭 상태 _s_4다. 시작 상태는 화살촉만 있는 화살표가 가리키는 것으로 표시하고, 매칭 상태는 이중 원으로 그린다.
머신은 입력 문자열을 한 번에 한 글자씩 읽으면서, 그 입력에 해당하는 화살표를 따라 상태를 옮긴다. 입력 문자열이 abbbba 라고 하자. 머신이 문자열의 첫 글자 a를 읽을 때 시작 상태 _s_0에 있다. a 화살표를 따라 _s_1로 간다. 나머지도 반복된다. b를 읽고 s2, b를 읽고 s3, b를 읽고 s2, b를 읽고 s3, 마지막으로 a를 읽고 s4로 간다.
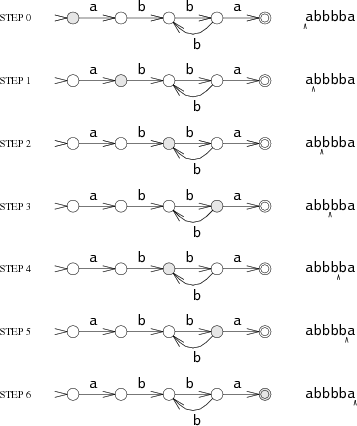
머신이 매칭 상태인 _s_4에서 끝나므로 문자열과 매칭된다. 비매칭 상태에서 끝나면 매칭되지 않는다. 실행 중 어느 시점이든 현재 입력 문자에 해당하는 화살표가 없으면 머신은 조기에 실행을 멈춘다.
지금까지의 머신은 결정적(deterministic) 유한 오토마타(DFA)다. 어떤 상태에서든 각 가능한 입력 문자는 최대 하나의 다음 상태로만 이어지기 때문이다. 다음 상태가 여러 개일 수 있는 머신도 만들 수 있다. 예를 들어 다음 머신은 앞의 것과 동치지만 결정적이지 않다.

이 머신이 결정적이지 않은 이유는 _s_2에서 b를 읽었을 때 다음 상태에 대한 선택지가 여러 개이기 때문이다. 또 다른 bb를 기대하며 _s_1로 돌아갈 수도 있고, 마지막 a를 기대하며 _s_3로 갈 수도 있다. 머신은 나머지 문자열을 미리 볼 수 없기 때문에 어떤 결정이 맞는지 알 방법이 없다. 이런 상황에서는 머신이 항상 맞게 추측한다 고 두는 것이 흥미롭다. 이런 머신을 비결정적 유한 오토마타(NFA 또는 NDFA)라고 한다. NFA는 문자열을 읽고 화살표를 따라가서 매칭 상태에 도달하는 어떤 방법이 하나라도 있으면 그 입력 문자열과 매칭된다.
때로는 입력 문자가 없는 화살표를 NFA에 두는 것이 편리하다. 이런 화살표는 라벨을 붙이지 않겠다. NFA는 언제든 입력을 읽지 않고도 라벨 없는 화살표를 따라갈 수 있다. 다음 NFA는 앞의 둘과 동치이며, 라벨 없는 화살표 덕분에 a(bb)+a 와의 대응이 가장 분명하다.

정규식과 NFA는 표현력 면에서 정확히 동치다. 모든 정규식에는 동치 NFA(같은 문자열들과 매칭)가 있고, 그 반대도 성립한다. (나중에 보겠지만 DFA도 NFA 및 정규식과 표현력이 동치다.) 정규식을 NFA로 번역하는 방법은 여러 가지가 있다. 여기서는 Thompson이 1968년 CACM 논문에서 처음 설명한 방법을 소개한다.
정규식의 NFA는 각 하위 표현식의 부분 NFA들을 조립해 만들며, 각 연산자마다 다른 구성법이 있다. 부분 NFA에는 매칭 상태가 없다. 대신 아무 것도 가리키지 않는 “매달린 화살표”가 하나 이상 있다. 구성 과정의 마지막에는 이 화살표들을 매칭 상태에 연결해 마무리한다.
한 글자를 매칭하는 NFA는 다음과 같다.
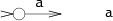
연결 _e_1 _e_2의 NFA는 _e_1 머신의 마지막 화살표를 _e_2 머신의 시작에 연결한다.
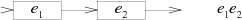
교대 _e_1|_e_2의 NFA는 새로운 시작 상태를 추가하고, 거기서 _e_1 머신 또는 _e_2 머신 중 하나를 선택하게 한다.
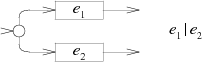
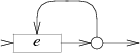
e?의 NFA는 e 머신과 빈 경로를 교대시킨다.
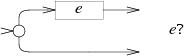
e*의 NFA는 같은 교대를 사용하되, _e_를 매칭한 뒤 다시 시작으로 되돌아가게 루프를 만든다.
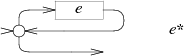
e+의 NFA도 루프를 만들지만, 적어도 한 번은 _e_를 통과하도록 강제한다.
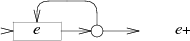
위 그림들에서 새 상태의 개수를 세어 보면, 이 기법은 괄호를 제외하고 정규식의 각 문자 또는 메타문자당 정확히 하나의 상태를 만든다. 따라서 최종 NFA의 상태 수는 원래 정규식 길이와 같거나 더 작다.
앞서 예제 NFA에서처럼 라벨 없는 화살표는 언제든 제거할 수 있고, 애초에 라벨 없는 화살표 없이 NFA를 생성하는 것도 가능하다. 하지만 라벨 없는 화살표는 NFA를 읽고 이해하기 쉽게 하고, C 표현도 단순하게 만들므로 여기서는 유지한다.
이제 정규식이 문자열과 매칭되는지 테스트하는 방법이 생겼다. 정규식을 NFA로 변환하고, 문자열을 입력으로 NFA를 실행하면 된다. 하지만 NFA는 선택지가 있을 때 “완벽하게 맞게 추측”할 수 있다고 가정한다. 일반 컴퓨터로 NFA를 실행하려면 이 추측을 시뮬레이션할 방법이 필요하다.
완벽한 추측을 시뮬레이션하는 한 가지 방법은 한 옵션을 추측해 보고, 실패하면 다른 옵션을 시도하는 것이다. 예를 들어 문자열 abbb에 대해 NFA abab|abbb를 실행하는 경우를 보자.
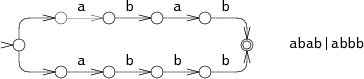
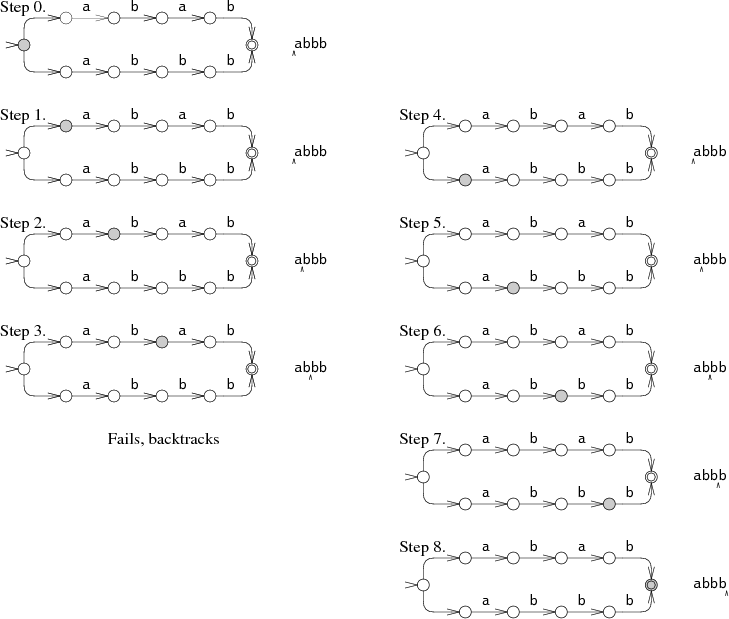
0단계에서 NFA는 선택을 해야 한다. abab를 매칭해 볼까, abbb를 매칭해 볼까? 그림에서는 NFA가 abab를 시도하지만 3단계 이후 실패한다. 그러면 NFA는 다른 선택을 시도하여 4단계로 이어지고 결국 매칭된다. 이 백트래킹 접근은 간단한 재귀 구현이 가능하지만, 성공할 때까지 입력 문자열을 여러 번 읽을 수 있다. 문자열이 매칭되지 않는다면, 포기하기 전에 가능한 실행 경로를 모두 시도해야 한다. 예제에서는 두 경로만 시도했지만, 최악의 경우 가능한 실행 경로 수가 지수적으로 많아질 수 있어 실행 시간이 매우 느려진다.
완벽한 추측을 시뮬레이션하는 더 효율적이지만 더 복잡한 방법은 두 옵션을 동시에 추측하는 것이다. 이 접근에서는 머신이 동시에 여러 상태에 있을 수 있게 시뮬레이션한다. 각 문자를 처리할 때, 해당 문자를 매칭하는 모든 화살표를 따라 모든 상태를 전진시킨다.
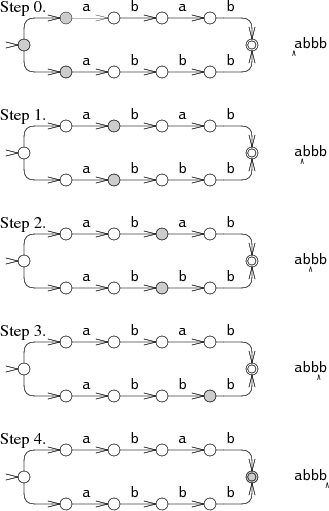
머신은 시작 상태와, 시작 상태에서 라벨 없는 화살표로 도달 가능한 모든 상태에서 시작한다. 1단계와 2단계에서 NFA는 동시에 두 상태에 있다. 3단계에서야 상태 집합이 하나로 좁혀진다. 이 다중 상태 접근은 두 경로를 동시에 시도하므로 입력을 한 번만 읽는다. 최악의 경우 NFA는 각 단계에서 모든 상태에 있을 수도 있지만, 이 경우에도 문자열 길이와 무관한(상태 수에만 비례하는) 상수량의 작업만 추가되므로 임의로 큰 입력도 선형 시간에 처리할 수 있다. 이는 백트래킹 접근의 지수 시간에 비해 극적인 개선이다. 효율의 핵심은 도달 가능한 상태들의 집합만 추적하고, 그 상태들에 도달하기 위해 어떤 경로를 썼는지는 추적하지 않는 데 있다. _n_개의 노드를 가진 NFA에서 어떤 단계든 도달 가능한 상태는 최대 _n_개지만, NFA를 통과하는 경로는 2^_n_개일 수 있다.
Thompson은 1968년 논문에서 다중 상태 시뮬레이션 접근을 소개했다. 그의 공식화에서는 NFA의 상태를 작은 머신 코드 시퀀스로 표현했고, 가능한 상태 목록은 함수 호출 명령들의 시퀀스였다. 본질적으로 Thompson은 정규식을 기발한 머신 코드로 컴파일했다. 40년이 지난 지금 컴퓨터는 훨씬 빨라졌고, 머신 코드 접근은 그만큼 필요하지 않다. 다음 절들은 이 알고리즘을 이식 가능한 ANSI C로 구현한 예를 제시한다. 전체 소스(400줄 미만)와 벤치마크 스크립트는 온라인에서 볼 수 있다. (C나 포인터에 익숙하지 않다면 설명만 읽고 실제 코드는 건너뛰어도 된다.)
첫 단계는 정규식을 동치 NFA로 컴파일하는 것이다. C 프로그램에서는 NFA를 State 구조체들의 연결 리스트 컬렉션으로 표현한다.
cstruct State { int c; State *out; State *out1; int lastlist; };
각 State는 c 값에 따라 다음 세 가지 NFA 조각 중 하나를 나타낸다.
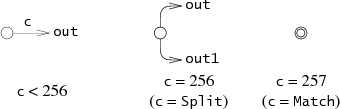
(lastlist는 실행 중에 사용되며 다음 절에서 설명한다.)
Thompson 논문을 따라, 컴파일러는 정규식을 후위(postfix) 표기법으로 바꾼 뒤, 연결 연산자를 명시적으로 나타내기 위해 점(.)을 추가한다. 별도의 함수 re2post가 중위(infix) 정규식 “a(bb)+a”를 동치 후위식 “abb.+.a.”로 변환한다. (실제 구현이라면 점을 연결 연산자가 아니라 “임의의 문자” 메타문자로 써야 할 것이다. 또한 실제 구현은 명시적 후위식을 만들기보다는 파싱 중에 NFA를 구성할 가능성이 높다. 하지만 후위식 버전은 편리하고 Thompson 논문을 더 가깝게 따른다.)
컴파일러가 후위식을 스캔할 때, 계산된 NFA 조각들의 스택을 유지한다. 리터럴은 새로운 NFA 조각을 스택에 푸시하고, 연산자는 조각을 팝한 다음 새 조각을 만들어 푸시한다. 예를 들어 abb.+.a.에서 abb를 컴파일한 뒤 스택에는 a, b, b에 대한 NFA 조각들이 있다. 그 다음의 .를 컴파일할 때 스택에서 두 b 조각을 팝하고, 연결 bb.에 대한 NFA 조각을 푸시한다. 각 NFA 조각은 시작 상태와 나가는 화살표들로 정의된다.
cstruct Frag { State *start; Ptrlist *out; };
start는 조각의 시작 상태를 가리키고, out은 아직 아무 데도 연결되지 않은 State* 포인터들의 포인터(State**)들로 구성된 리스트다. 이것들이 NFA 조각의 매달린 화살표에 해당한다.
포인터 리스트를 다루는 보조 함수들:
cPtrlist *list1(State **outp); Ptrlist *append(Ptrlist *l1, Ptrlist *l2); void patch(Ptrlist *l, State *s);
list1은 단일 포인터 outp를 담은 새 포인터 리스트를 만든다. append는 두 포인터 리스트를 이어 붙여 결과를 반환한다. patch는 포인터 리스트 l에 있는 매달린 화살표들을 상태 s에 연결한다. 즉 l의 각 포인터 outp에 대해 *outp = s를 수행한다.
이 기본 연산들과 조각 스택이 있으면, 컴파일러는 후위식에 대한 간단한 루프가 된다. 끝에는 하나의 조각만 남고, 여기에 매칭 상태를 패치해서 NFA를 완성한다.
cState* post2nfa(char *postfix) { char *p; Frag stack[1000], *stackp, e1, e2, e; State *s; #define push(s) *stackp++ = s #define pop() *--stackp stackp = stack; for(p=postfix; *p; p++){ switch(*p){ /* 컴파일 케이스들: 아래에서 설명 */ } } e = pop(); patch(e.out, matchstate); return e.start; }
구체적인 컴파일 케이스는 앞에서 설명한 번역 단계를 그대로 따른다.
리터럴 문자:
cdefault: s = state(*p, NULL, NULL); push(frag(s, list1(&s->out))); break;
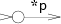
연결:
ccase '.': e2 = pop(); e1 = pop(); patch(e1.out, e2.start); push(frag(e1.start, e2.out)); break;

교대:
ccase '|': e2 = pop(); e1 = pop(); s = state(Split, e1.start, e2.start); push(frag(s, append(e1.out, e2.out))); break;
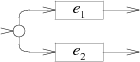
0 또는 1:
ccase '?': e = pop(); s = state(Split, e.start, NULL); push(frag(s, append(e.out, list1(&s->out1)))); break;
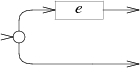
0개 이상:
ccase '*': e = pop(); s = state(Split, e.start, NULL); patch(e.out, s); push(frag(s, list1(&s->out1))); break;
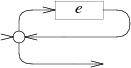
1개 이상:
ccase '+': e = pop(); s = state(Split, e.start, NULL); patch(e.out, s); push(frag(e.start, list1(&s->out1))); break;
이제 NFA가 만들어졌으니 시뮬레이션을 해야 한다. 시뮬레이션은 State 집합들을 추적해야 하며, 간단한 배열 리스트로 저장한다.
cstruct List { State **s; int n; };
시뮬레이션은 두 리스트를 사용한다. clist는 현재 NFA가 있을 수 있는 상태 집합이고, nlist는 현재 문자를 처리한 뒤의 다음 상태 집합이다. 실행 루프는 clist를 시작 상태만 포함하도록 초기화하고, 한 단계씩 머신을 실행한다.
cint match(State *start, char *s) { List *clist, *nlist, *t; /* l1과 l2는 사전 할당된 전역 */ clist = startlist(start, &l1); nlist = &l2; for(; *s; s++){ step(clist, *s, nlist); t = clist; clist = nlist; nlist = t; /* clist, nlist 교환 */ } return ismatch(clist); }
루프의 매 반복마다 할당을 피하기 위해, match는 미리 할당된 리스트 l1, l2를 clist, nlist로 사용하고 매 단계 뒤 두 개를 스왑한다.
최종 상태 리스트에 매칭 상태가 포함되면 문자열은 매칭된다.
cint ismatch(List *l) { int i; for(i=0; i<l->n; i++) if(l->s[i] == matchstate) return 1; return 0; }
addstate는 상태를 리스트에 추가하되, 이미 리스트에 있으면 추가하지 않는다. 매번 리스트 전체를 스캔하면 비효율적이므로 listid라는 변수를 리스트 생성 번호로 쓴다. addstate가 s를 리스트에 넣을 때 s->lastlist에 listid를 기록한다. 둘이 이미 같으면 s는 현재 만들고 있는 리스트에 이미 들어 있다는 뜻이다. 또한 addstate는 라벨 없는 화살표를 따라간다. s가 Split 상태라면 새 상태로 가는 두 개의 라벨 없는 화살표가 있으므로, s 대신 그 두 상태를 리스트에 추가한다.
cvoid addstate(List *l, State *s) { if(s == NULL || s->lastlist == listid) return; s->lastlist = listid; if(s->c == Split){ /* 라벨 없는 화살표 따라가기 */ addstate(l, s->out); addstate(l, s->out1); return; } l->s[l->n++] = s; }
startlist는 시작 상태 하나만 더해서 초기 상태 리스트를 만든다.
cList* startlist(State *s, List *l) { listid++; l->n = 0; addstate(l, s); return l; }
마지막으로 step은 한 문자만큼 NFA를 전진시킨다. 현재 리스트 clist로부터 다음 리스트 nlist를 계산한다.
cvoid step(List *clist, int c, List *nlist) { int i; State *s; listid++; nlist->n = 0; for(i=0; i<clist->n; i++){ s = clist->s[i]; if(s->c == c) addstate(nlist, s->out); } }
위에서 설명한 C 구현은 성능을 염두에 두고 작성한 것이 아니다. 그럼에도 선형 시간 알고리즘의 느린 구현은, 지수 시간 알고리즘의 빠른 구현을 지수가 충분히 커지면 쉽게 이길 수 있다. 다양한 인기 정규식 엔진을 이른바 병적 정규식으로 테스트하면 이를 잘 보여준다.
정규식 a?nan를 생각하자. 이는 a?들이 아무 것도 매칭하지 않도록 선택하면 문자열 an과 매칭된다. 그러면 전체 문자열은 an이 매칭한다. 백트래킹 정규식 구현은 0 또는 1 ?를 “먼저 1을 시도하고, 그 다음 0을 시도”하는 방식으로 구현한다. 이런 선택이 _n_개 있으므로 총 2^n 가지 가능성이 있다. 매칭으로 이어지는 경우는 마지막 하나—모든 ?에 대해 0을 고르는 경우—뿐이다. 따라서 백트래킹은 O(2^n) 시간이 필요해 n=25를 크게 넘기기 어렵다.
반면 Thompson 알고리즘은 길이가 대략 _n_인 상태 리스트를 유지하며, 길이가 _n_인 문자열을 처리하므로 총 O(n^2) 시간이 든다. (정규식을 고정하지 않고 입력과 함께 키우고 있기 때문에 실행 시간이 초선형이다. 길이 _m_의 정규식을 길이 _n_의 텍스트에 적용하면 Thompson NFA는 O(mn) 시간이다.)
다음 그래프는 a?nan이 an과 매칭되는지 확인하는 데 걸리는 시간을 그린 것이다.
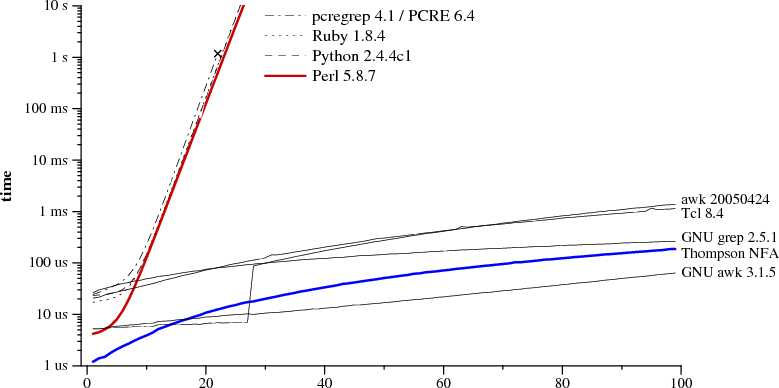
정규식과 텍스트 크기 n
a?nan 를 an 에 매칭
그래프의 _y_축은 로그 스케일로, 다양한 시간 범위를 한 그래프에서 보기 위함이다.
그래프를 보면 Perl, PCRE, Python, Ruby 모두 재귀적 백트래킹을 사용함이 분명하다. PCRE는 n=23에서 올바른 답을 내지 못하는데, 최대 단계 수를 넘으면 재귀 백트래킹을 중단하기 때문이다. Perl 5.6부터 Perl의 정규식 엔진은 재귀 백트래킹 탐색을 메모이제이션한다고 알려져 있다. 이는 메모리 비용을 치르면 역참조가 없을 때 지수 폭발을 막아야 한다. 하지만 성능 그래프는 메모이제이션이 완전하지 않음을 보여준다. 표현식에 역참조가 없어도 Perl의 실행 시간은 지수적으로 증가한다. 여기서 벤치마크하진 않았지만 Java도 백트래킹 구현을 쓴다. 사실 java.util.regex 인터페이스는 매칭 경로에 임의의 Java 코드를 끼워 넣을 수 있기 때문에 백트래킹 구현을 요구한다. PHP는 PCRE 라이브러리를 사용한다.
두꺼운 파란 선은 앞서 제시한 Thompson 알고리즘의 C 구현이다. Awk, Tcl, GNU grep, GNU awk는 DFA를 만들며, 사전 계산하거나 다음 절에서 설명하는 즉석(on-the-fly) 구성으로 만든다.
일부는 이 테스트가 백트래킹 구현에 불공정하다고 주장할지 모른다. 흔치 않은 코너 케이스에 집중한다는 이유에서다. 하지만 이는 핵심을 놓친 주장이다. 모든 입력에서 예측 가능하고 일관되게 빠른 구현과, 대개는 빠르지만 어떤 입력에서는 CPU 시간이 수년(또는 그 이상) 걸릴 수 있는 구현 중에서 선택해야 한다면 결정은 쉬워야 한다. 또한 이런 극단적 예가 실무에서 자주 나오지는 않지만, 덜 극단적인 예는 실제로 발생한다. 예컨대 공백으로 구분된 5개 필드를 분리하기 위해 (.*)(.*)(.*)(.*)(.*)를 쓰거나, 공통 케이스를 먼저 나열하지 않은 교대를 쓰는 경우가 그렇다. 그 결과 프로그래머들은 어떤 구성 요소가 비싼지 배우고 피하거나, 이른바 최적화 도구에 의존하게 된다. Thompson의 NFA 시뮬레이션을 사용하면 이런 적응이 필요 없다. 비싼 정규식이 존재하지 않기 때문이다.
DFA는 NFA보다 실행이 더 효율적이라는 점을 떠올려 보자. DFA는 한 번에 하나의 상태에만 있기 때문에(다음 상태 선택이 없기 때문에) 그렇다. 모든 NFA는 동치 DFA로 변환할 수 있는데, 이때 DFA의 각 상태는 NFA 상태 리스트에 대응한다.
예를 들어 앞에서 abab|abbb에 사용했던 NFA에 상태 번호를 추가해 보자.
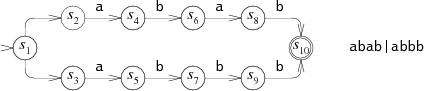
이에 대응하는 DFA는 다음과 같다.
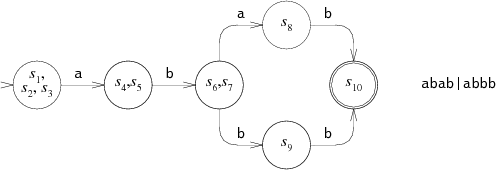
DFA의 각 상태는 NFA의 상태 리스트에 대응한다.
어떤 의미에서는 Thompson의 NFA 시뮬레이션은 동치 DFA를 실행하고 있는 셈이다. 각 List는 어떤 DFA 상태에 대응하고, step 함수는 “리스트와 다음 문자”가 주어졌을 때 들어갈 다음 DFA 상태를 계산한다. Thompson 알고리즘은 필요한 순간마다 각 DFA 상태를 재구성함으로써 DFA를 시뮬레이션한다. 이 작업을 매 단계 후에 버리지 말고 여분의 메모리에 List를 캐시해 두면, 미래에 같은 계산을 반복하는 비용을 피할 수 있고 사실상 필요한 만큼만 동치 DFA를 계산하는 셈이 된다. 이 절은 그런 접근의 구현을 제시한다. 앞 절의 NFA 구현에 100줄도 안 되는 코드를 더하면 DFA 구현을 만들 수 있다.
캐시를 구현하기 위해, 먼저 DFA 상태를 나타내는 새 타입을 도입한다.
cstruct DState { List l; DState *next[256]; DState *left; DState *right; };
DState는 리스트 l의 캐시된 복사본이다. next 배열은 가능한 각 입력 문자에 대한 다음 상태 포인터를 담는다. 현재 상태가 d이고 다음 입력 문자가 c이면 d->next[c]가 다음 상태다. d->next[c]가 NULL이면 아직 계산되지 않은 것이다. nextstate는 주어진 상태와 문자에 대해 다음 상태를 계산하고 기록하고 반환한다.
정규식 매칭은 d->next[c]를 반복해서 따라가며, 필요할 때 nextstate로 새 상태를 계산한다.
cint match(DState *start, char *s) { int c; DState *d, *next; d = start; for(; *s; s++){ c = *s & 0xFF; if((next = d->next[c]) == NULL) next = nextstate(d, c); d = next; } return ismatch(&d->l); }
계산된 모든 DState는 “List로 DState를 찾을 수 있는” 구조에 저장해야 한다. 이를 위해 List를 정렬한 것을 키로 하는 이진 트리를 사용한다. dstate 함수는 주어진 List에 대한 DState를 반환하며, 필요하다면 할당한다.
cDState* dstate(List *l) { int i; DState **dp, *d; static DState *alldstates; qsort(l->s, l->n, sizeof l->s[0], ptrcmp); /* 트리에서 기존 DState 찾기 */ dp = &alldstates; while((d = *dp) != NULL){ i = listcmp(l, &d->l); if(i < 0) dp = &d->left; else if(i > 0) dp = &d->right; else return d; } /* 새 DState 할당 및 초기화 */ d = malloc(sizeof *d + l->n*sizeof l->s[0]); memset(d, 0, sizeof *d); d->l.s = (State**)(d+1); memmove(d->l.s, l->s, l->n*sizeof l->s[0]); d->l.n = l->n; /* 트리에 삽입 */ *dp = d; return d; }
nextstate는 NFA의 step을 실행하고 대응하는 DState를 반환한다.
cDState* nextstate(DState *d, int c) { step(&d->l, c, &l1); return d->next[c] = dstate(&l1); }
마지막으로 DFA의 시작 상태는 NFA의 시작 리스트에 대응하는 DState다.
cDState* startdstate(State *start) { return dstate(startlist(start, &l1)); }
(NFA 시뮬레이션과 마찬가지로 l1은 미리 할당된 List다.)
DState들은 DFA 상태에 대응하지만 DFA는 필요할 때만 만들어진다. 검색 중에 한 번도 만나지 않은 DFA 상태는 캐시에 존재하지 않는다. 대안으로는 전체 DFA를 한 번에 계산할 수 있다. 그러면 match에서 조건 분기를 제거해 조금 더 빨라지지만, 시작 시간과 메모리 사용량이 늘어난다.
즉석 DFA 구성에서 메모리 사용량을 제한할 수 있는지 걱정할 수도 있다. DState들은 step 함수의 캐시일 뿐이므로, 캐시가 너무 커지면 dstate 구현이 지금까지의 DFA 전체를 버리도록 선택할 수도 있다. 이런 캐시 교체 정책은 dstate와 nextstate에 몇 줄의 코드만 더하면 되고, 메모리 관리 코드 약 50줄 정도가 추가로 필요하다. 구현은 온라인에서 볼 수 있다. (Awk는 비슷한 제한 크기 캐시 전략을 사용하며, 캐시된 상태를 32개로 고정한다. 이것이 위 그래프에서 n=28에서 성능이 불연속적으로 바뀌는 이유다.)
정규식에서 유도된 NFA는 대체로 좋은 지역성(locality)을 보인다. 대부분의 텍스트에서 실행할 때 같은 상태를 반복 방문하고 같은 전이 화살표를 반복해서 따라가기 때문이다. 그래서 캐싱은 가치가 있다. 어떤 화살표를 처음 따라갈 때는 NFA 시뮬레이션처럼 다음 상태를 계산해야 하지만, 이후에는 메모리 접근 한 번이면 된다. 실제 DFA 기반 구현은 추가 최적화를 통해 더 빠르게 실행될 수 있다. (아직 쓰이지 않은) 동반 글에서는 DFA 기반 정규식 구현을 더 자세히 다룰 예정이다.
실제 프로그램에서의 정규식 사용은 위에서 설명한 구현들이 처리하는 것보다 조금 더 복잡하다. 이 절은 흔한 복잡 요소들을 간단히 설명한다. 어느 하나라도 완전한 설명은 이 입문 글의 범위를 벗어난다.
문자 클래스. [0-9]나 \w나 .(점) 같은 문자 클래스는 교대의 간결한 표현일 뿐이다. 컴파일 과정에서 교대로 확장할 수 있지만, 이를 명시적으로 표현하는 새 종류의 NFA 노드를 추가하는 것이 더 효율적이다. POSIX는 로케일에 따라 의미가 바뀌는 [[:upper:]] 같은 특수 문자 클래스를 정의하지만, 이를 수용하는 어려운 부분은 의미를 결정하는 것이지 NFA에 그 의미를 인코딩하는 것이 아니다.
이스케이프 시퀀스. 실제 정규식 문법은 메타문자(\(, \), \\ 등)를 매칭하기 위한 방법으로도, \n 같은 입력하기 어려운 문자를 지정하는 방법으로도 이스케이프 시퀀스를 처리해야 한다.
카운트된 반복. 많은 정규식 구현은 정확히 _n_번 반복을 나타내는 {n}을 제공한다. 또한 {n,m}는 최소 _n_번 최대 _m_번, {n,}는 _n_번 이상을 뜻한다. 재귀 백트래킹 구현은 루프를 써서 이를 구현할 수 있다. NFA 또는 DFA 기반 구현은 반복을 확장해야 한다. e{3}는 _eee_로 확장된다. e{3,5}는 eeee?e?로, e{3,}는 eee+로 확장된다.
서브매치 추출. 정규식을 문자열 분리나 파싱에 사용할 때, 입력 문자열의 어느 구간이 각 하위 표현식에 의해 매칭되었는지 알아내는 것이 유용하다. ([0-9]+-[0-9]+-[0-9]+)([0-9]+:[0-9]+) 같은 정규식이 문자열(예: 날짜와 시간)을 매칭한 뒤, 많은 정규식 엔진은 각 괄호식이 매칭한 텍스트를 제공한다. 예를 들어 Perl에서는 다음과 같이 쓸 수 있다.
perlif(/([0-9]+-[0-9]+-[0-9]+) ([0-9]+:[0-9]+)/){ print "date: $1, time: $2\n"; }
서브매치 경계 추출은 이론가들에게 대체로 무시되어 왔고, 재귀 백트래킹을 쓰는 가장 설득력 있는 이유로 자주 언급된다. 하지만 Thompson 스타일 알고리즘도 효율을 유지하면서 서브매치 경계를 추적하도록 변형할 수 있다. Unix 8판의 regexp(3) 라이브러리는 1985년에 이미 그런 알고리즘을 구현했지만, 아래에서 설명하듯 널리 쓰이거나 주목받지는 못했다.
비고정(unanchored) 매칭. 이 글은 정규식이 입력 문자열 전체와 매칭된다고 가정했다. 실제로는 입력의 어떤 부분 문자열이 정규식과 매칭되는지 찾고 싶을 때가 많다. 전통적인 Unix 도구는 입력에서 가장 왼쪽에서 시작하는 매칭 중 가장 긴 부분 문자열을 반환한다. _e_의 비고정 검색은 서브매치 추출의 특수한 경우다. .*(e).*를 찾는 것과 같지만, 앞의 .*는 가능한 한 짧게 매칭하도록 제약된다.
비탐욕(non-greedy) 연산자. 전통적인 Unix 정규식에서 ?, *, +는 전체 정규식이 매칭되는 범위 안에서 가능한 한 많이 매칭하도록 정의된다. (.+)(.+)를 abcd에 매칭하면 첫 (.+)는 abc, 둘째는 d를 매칭한다. 이런 연산자를 이제 탐욕적(greedy) 이라고 부른다. Perl은 ??, *?, +?를 비탐욕 버전으로 도입했는데, 전체 매칭을 유지하면서 가능한 한 적게 매칭한다. (.+?)(.+?)를 abcd에 매칭하면 첫 (.+?)는 a만, 둘째는 bcd를 매칭한다. 정의상, 연산자가 탐욕적인지 여부는 문자열 전체가 정규식과 매칭되는지 여부에는 영향을 줄 수 없고, 오직 서브매치 경계 선택에만 영향을 준다. 백트래킹 알고리즘은 비탐욕 연산자를 간단히 구현할 수 있다. 긴 매치보다 짧은 매치를 먼저 시도하면 된다. 예를 들어 일반 백트래킹 구현에서 e?는 먼저 _e_를 쓰는 경우를 시도하고 그 다음 안 쓰는 경우를 시도한다. e??는 그 순서가 반대다. Thompson 알고리즘의 서브매치 추적 변형도 비탐욕 연산자를 수용하도록 조정할 수 있다.
단언(assertion). 전통적인 메타문자 ^와 $는 주변 텍스트에 대한 단언 으로 볼 수 있다. ^는 이전 문자가 개행(또는 문자열 시작)임을 단언하고, $는 다음 문자가 개행(또는 문자열 끝)임을 단언한다. Perl은 단어 경계 \b 같은 단언을 추가했는데, 이는 이전 문자가 영숫자이고 다음이 아니거나 그 반대임을 단언한다. Perl은 이를 더 일반화해 룩어헤드(lookahead) 단언 같은 임의 조건을 도입했다. (?=re)는 현재 입력 위치 이후의 텍스트가 _re_와 매칭됨을 단언하지만 실제로 입력 위치를 전진시키지 않는다. (?!re)는 반대로 매칭되지 않음을 단언한다. 룩비하인드(lookbehind) (?<=re), (?<!re)는 현재 위치 이전 텍스트에 대해 비슷한 단언을 한다. ^, $, \b 같은 단순 단언은 NFA에 수용하기 쉽고(전방 단언은 매치를 1바이트 지연시키는 식으로), 일반화된 단언은 더 어렵지만 원칙적으로는 NFA에 인코딩할 수 있다.
역참조. 앞서 말했듯, 역참조가 있는 정규식을 효율적으로 구현하는 방법은 아무도 모른다(불가능하다고 증명한 사람도 없다). 보다 정확히 말하면 이 문제는 NP-완전인데, 누군가 효율적 구현을 찾는다면 컴퓨터 과학계에 중대한 뉴스가 될 것이고 백만 달러 상을 받을 만한 일이다. 원래 awk와 egrep이 택했던 가장 단순하고 효과적인 전략은 역참조를 구현하지 않는 것이었다. 하지만 이제는 현실적이지 않다. 사용자들이 적어도 가끔은 역참조에 의존하며, 역참조는 POSIX 정규식 표준의 일부이기 때문이다. 그럼에도 대부분의 정규식에 Thompson NFA 시뮬레이션을 쓰고, 역참조가 필요할 때만 백트래킹을 꺼내 쓰는 것은 합리적이다. 특히 영리한 구현이라면 둘을 결합해 역참조를 수용하기 위해서만 백트래킹으로 후퇴할 수 있다.
메모이제이션을 동반한 백트래킹. 가능할 때 백트래킹 중 지수적 폭발을 피하기 위해 메모이제이션을 쓰는 Perl의 접근은 좋은 방법이다. 최소한 이론적으로는 Perl 정규식이 백트래킹보다는 NFA에 더 가까운 동작을 하게 해야 한다. 하지만 메모이제이션이 문제를 완전히 해결하는 것은 아니다. 메모이제이션 자체가 텍스트 크기 × 정규식 크기 정도의 메모리를 요구한다. 또한 백트래킹이 쓰는 스택 공간 문제(텍스트 크기에 선형)를 해결하지 못한다. 긴 문자열을 매칭하면 백트래킹 구현은 흔히 스택을 초과한다.
sh$ perl -e '("a" x 100000) =~ /^(ab?)*$/;' Segmentation fault (core dumped) $
문자 집합. 현대 정규식 구현은 유니코드 같은 큰 비ASCII 문자 집합을 다뤄야 한다. Plan 9 정규식 라이브러리는 NFA를 실행할 때 각 단계의 입력 문자를 하나의 유니코드 문자로 처리함으로써 유니코드를 통합한다. 이 라이브러리는 NFA 실행과 입력 디코딩을 분리하여, 같은 정규식 매칭 코드가 UTF-8과 와이드 문자 입력 모두에 쓰이게 한다.
Michael Rabin과 Dana Scott는 1959년에 비결정적 유한 오토마타와 비결정성 개념을 소개했고 [7], NFA가 각 DFA 상태가 NFA 상태 집합에 대응하는(잠재적으로 훨씬 큰) DFA로 시뮬레이션될 수 있음을 보였다. (그들은 이 논문에서 비결정성 개념을 도입한 공로로 1976년 튜링상을 받았다.)
R. McNaughton과 H. Yamada[4] 및 Ken Thompson [9]은 정규식을 NFA로 변환하는 최초의 구성을 제시한 것으로 흔히 인정받는다. 다만 두 논문 모두 당시 막 태동한 NFA 개념을 직접 언급하지는 않는다. McNaughton과 Yamada의 구성은 DFA를 만들고, Thompson의 구성은 IBM 7094용 머신 코드를 만든다. 하지만 두 논문을 곱씹어 보면 둘 다 NFA 구성이 잠재적으로 깔려 있음을 알 수 있다. 정규식을 NFA로 바꾸는 구성들은 NFA가 해야 하는 선택을 어떻게 인코딩하느냐만 다르다. 위에서 사용한(Thompson을 모방한) 접근은 명시적 선택 노드(Split 노드)와 라벨 없는 화살표로 선택을 인코딩한다. 흔히 McNaughton–Yamada에 귀속되는 다른 접근은 라벨 없는 화살표를 피하고, 대신 같은 라벨을 가진 여러 outgoing 화살표를 NFA 상태에 허용한다. McIlroy [3]는 이 접근을 Haskell로 특히 우아하게 구현했다.
Thompson의 정규식 구현은 IBM 7094에서 CTSS [10] 운영체제 위에서 동작하던 QED 편집기용이었다. 편집기 사본은 archived CTSS 소스 [5]에서 찾을 수 있다. L. Peter Deutsch와 Butler Lampson [1]이 첫 QED를 개발했지만, Thompson의 재구현이 정규식을 사용한 첫 구현이었다. 또 다른 QED 구현의 저자 Dennis Ritchie는 QED 편집기의 초기 역사를 문서화했다 [8]. (Thompson, Ritchie, Lampson은 이후 QED나 유한 오토마타와 무관한 작업으로 튜링상을 받았다.)
Thompson의 논문은 긴 정규식 구현 계보의 시작점이 되었다. 하지만 Thompson은 First Edition Unix(1971)에 등장한 ed나, 그 후손인 grep(처음은 Fourth Edition, 1973)을 구현할 때 자신의 알고리즘을 쓰지 않았다. 대신 이 오래된 Unix 도구들은 재귀적 백트래킹을 썼다. 당시 정규식 문법이 매우 제한적이었기 때문에(그룹 괄호와 |, ?, + 연산자가 없었음) 백트래킹은 정당화될 수 있었다. Seventh Edition(1979)에 처음 등장한 Al Aho의 egrep은 전체 정규식 문법을 제공한 첫 Unix 도구였고, 사전 계산된 DFA를 사용했다. Eighth Edition(1985)에서는 egrep이 위에서 소개한 구현처럼 즉석에서 DFA를 계산했다.
1980년대 초 텍스트 편집기 sam [6]을 쓰던 Rob Pike는 새로운 정규식 구현을 작성했고, Dave Presotto가 이를 라이브러리로 뽑아 Eighth Edition에 포함시켰다. Pike의 구현은 서브매치 추적을 효율적인 NFA 시뮬레이션에 통합했지만, Eighth Edition 소스 전체가 널리 배포되지 않았기 때문에 널리 쓰이거나 알려지지 못했다. Pike 자신도 자신의 기법이 새로운 것이라고 생각하지 못했다. Henry Spencer는 Eighth Edition 라이브러리 인터페이스를 처음부터 재구현했는데, 백트래킹을 사용했고, 이를 퍼블릭 도메인으로 공개했다. 이 구현은 매우 널리 쓰였고, 결국 앞에서 언급한 느린 정규식 구현들(Perl, PCRE, Python 등)의 기반이 되었다. (Spencer를 변호하자면, 그는 루틴이 느릴 수 있다는 것을 알고 있었고 더 효율적 알고리즘의 존재를 몰랐다. 그는 문서에서 “많은 사용자가 속도가 충분하다고 느꼈지만, egrep의 내부를 이 코드로 교체하는 것은 실수일 것이다”라고 경고하기도 했다.) Unicode를 지원하도록 확장된 Pike의 정규식 구현은 sam과 함께 1992년 말에 자유롭게 제공되었지만, 특히 효율적인 정규식 검색 알고리즘은 주목받지 못했다. 이 코드는 이제 여러 형태로 उपलब्ध하다. sam의 일부로, Plan 9 정규식 라이브러리로, 또는 Unix용으로 별도 패키징되어 있다. Ville Laurikari는 1999년에 Pike 알고리즘을 독립적으로 재발견했고, 이론적 기반도 구축했다 [2].
마지막으로, 정규식에 대한 논의에서 Jeffrey Friedl의 책 _Mastering Regular Expressions_를 빼놓을 수 없다. 이는 오늘날 프로그래머들에게 가장 인기 있는 참고서 중 하나다. Friedl의 책은 오늘날의 정규식 구현을 어떻게 쓰는 게 좋은지 가르치지만, 어떻게 구현하는 게 좋은지는 다루지 않는다. 구현 문제에 할애된 적은 분량마저도 “재귀 백트래킹만이 NFA를 시뮬레이션하는 유일한 방법”이라는 널리 퍼진 믿음을 강화한다. Friedl은 자신이 기반 이론을 이해하지 못하고 존중하지도 않는다는 점을 분명히 한다.
유한 오토마타 기반 기법을 사용하면 정규식 매칭은 수십 년 전부터 알려진 방식으로 단순하고 빠를 수 있다. 반면 Perl, PCRE, Python, Ruby, Java 등 많은 언어는 단순하지만 극단적으로 느려질 수 있는 재귀 백트래킹 기반 구현을 사용한다. 역참조를 제외하면, 느린 백트래킹 구현이 제공하는 기능은 오토마타 기반 구현에서도 훨씬 더 빠르고 일관된 속도로 제공할 수 있다.
이 시리즈의 다음 글 “정규식 매칭: 가상 머신 접근”은 NFA 기반 서브매치 추출을 논의한다. 세 번째 글 “현실 세계의 정규식 매칭”은 실제 제품 수준 구현을 살펴본다. 네 번째 글 “트라이그램 인덱스로 정규식 매칭”은 Google Code Search가 어떻게 구현되었는지 설명한다.
Lee Feigenbaum, James Grimmelmann, Alex Healy, William Josephson, Arnold Robbins가 이 글의 초안을 읽고 많은 유익한 제안을 해 주었다. Rob Pike는 자신의 정규식 구현과 관련된 역사 일부를 명확히 해 주었다. 모두에게 감사한다.
[1] L. Peter Deutsch, Butler Lampson, “An online editor,” Communications of the ACM 10(12) (1967년 12월), 793–799쪽. http://doi.acm.org/10.1145/363848.363863
[2] Ville Laurikari, “NFAs with Tagged Transitions, their Conversion to Deterministic Automata and Application to Regular Expressions,” Symposium on String Processing and Information Retrieval, 2000년 9월. http://laurikari.net/ville/spire2000-tnfa.ps
[3] M. Douglas McIlroy, “Enumerating the strings of regular languages,” Journal of Functional Programming 14 (2004), 503–518쪽. http://www.cs.dartmouth.edu/~doug/nfa.ps.gz (프리프린트)
[4] R. McNaughton, H. Yamada, “Regular expressions and state graphs for automata,” IRE Transactions on Electronic Computers EC-9(1) (1960년 3월), 39–47쪽.
[5] Paul Pierce, “CTSS source listings.” http://www.piercefuller.com/library/ctss.html (Thompson의 QED는 소스 목록 아카이브의 com5 파일에 있고 0QED로 표시되어 있음)
[6] Rob Pike, “The text editor sam,” Software—Practice & Experience 17(11) (1987년 11월), 813–845쪽. http://plan9.bell-labs.com/sys/doc/sam/sam.html
[7] Michael Rabin, Dana Scott, “Finite automata and their decision problems,” IBM Journal of Research and Development 3 (1959), 114–125쪽. http://www.research.ibm.com/journal/rd/032/ibmrd0302C.pdf
[8] Dennis Ritchie, “An incomplete history of the QED text editor.” http://plan9.bell-labs.com/~dmr/qed.html
[9] Ken Thompson, “Regular expression search algorithm,” Communications of the ACM 11(6) (1968년 6월), 419–422쪽. http://doi.acm.org/10.1145/363347.363387 (PDF)
[10] Tom Van Vleck, “The IBM 7094 and CTSS.” http://www.multicians.org/thvv/7094.html
reddit, perlmonks, LtU에서의 토론:
Copyright © 2007 Russ Cox. All Rights Reserved.