1983년 FLP 정리는 비동기 결정적 모델에서 하나의 결함을 허용하는 분산 합의 프로토콜이 유한 시간 내 합의를 보장할 수 없음을 보인다. 이 글은 상태 그래프와 메시지 전달 순서의 교환성을 이용한 핵심 아이디어를 직관적으로 설명하고, 모델 가정의 의미와 실무적 함의를 간략히 논의한다.
“FLP”(Fischer–Lynch–Paterson) 정리는 분산 합의(distributed consensus)1에 관한 불가능성 결과로, 1983년 논문 Impossibility of Distributed Consensus with One Faulty Process에서 제시되었다. 이 정리는 특정 모델에서, 한 노드가 다운되어도 합의를 달성할 수 있는 시스템은 유한한 시간 안에 합의 달성을 보장할 수 없다고 말한다. 여기서는 증명의 핵심 아이디어를 설명한다. 아이디어 자체는 꽤 직관적이며 — 세부의 대부분은 이를 형식화하는 데 관한 것이다.
모델은 꽤 단순하다. 여러 컴퓨터가 있고, 서로에게 메시지를 보낸다. 메시지는 임의로 재정렬되거나 지연될 수 있다. 전역 시계나 무작위성은 없다 — 컴퓨터는 결정적으로 동작하며, 유일한 비결정성의 원천은 메시지가 도착하는 방식뿐이다.
전체 시스템의 가능한 상태들과 그 사이의 전이를 고려하자. 컴퓨터가 결정적이므로, 시스템 상태를 바꿀 수 있는 유일한 사건은 컴퓨터가 메시지를 "수신"하는 것이다. 컴퓨터가 메시지를 받으면, 자신의 로컬 상태를 바꾸고 그에 대한 응답으로 새 메시지들을 보낼 수 있다.
타임아웃이 없다는 점에 주의하자. 이는 예컨대 한 컴퓨터가 메시지를 하나 보내고, 일정 시간 내 응답이 없으면 다른 메시지를 보내 복구하는 식의 동작을 할 수 없음을 의미한다. 복구 메시지를 보내고 싶다면, 사실상 원래 메시지와 동시에, 곧바로 복구 메시지도 보내야 한다는 뜻이다2.
가능한 모든 시스템 상태를 그래프로 그릴 수 있다. 상태 A에서 상태 B로 전이가 가능하면(즉, 상태 A에서 이미 전송된 메시지 중 하나를 수신하면 시스템이 상태 B로 이동한다면) A에서 B로 가는 화살표를 그린다. 그래프의 각 노드가 나타내는 전체 상태는 각 컴퓨터의 내부 상태와 아직 수신되지 않은 메시지들의 집합을 포함한다.
합의 프로토콜의 가능한 결과가 두 가지, 빨강(red)과 파랑(blue)이라고 하자. 그래프의 각 노드를 그 결과에 따라 색칠한다. 합의에 도달한 노드는 빨강 또는 파랑, 아직 도달하지 않은 노드는 회색(gray)이다. 이것이 합의 시스템이라는 사실은 빨강 노드에서 도달 가능한 모든 노드도 빨강이어야 함을 의미한다(파랑도 마찬가지). 일단 시스템이 어떤 결정을 내리면, 그 결정을 무를 수는 없다.
오직 빨강 노드들로만 도달 가능한 노드는 그 자신도 빨강이어야 한다는 점에 주목하자 — 참여자들 누구도 아직 모르고 있을 수는 있어도, 가능한 모든 결과가 빨강이라면 시스템은 이미 합의에 도달한 것이다.
그래프는 대략 다음과 같이 생겼을 수 있다(대부분의 실용적인 합의 알고리즘에서는 상태 공간이 사실상 무한으로 다뤄지긴 한다):
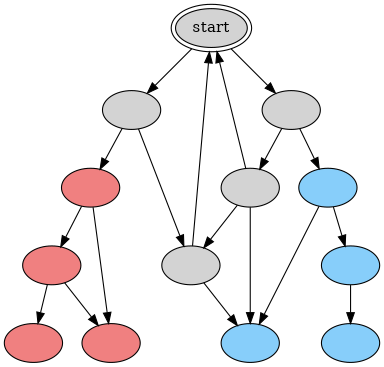
정리가 말하는 바는 이렇다. 결함 허용 합의 프로토콜에서는, 어떤 회색 노드에서 시작하더라도 항상 무한한 회색 경로가 존재한다 — 메시지 스케줄링의 적어도 한 방식은 영원히 합의에 도달하지 못하게 만들 수 있다. 동치로, 모든 회색 노드는 회색 노드로 향하는 간선을 적어도 하나 갖는다.
이를 보이기 위해, 회색 노드 G가 회색 노드로의 전이를 하나도 갖지 않는다고 가정하자. 이는 G에서 나가는 모든 간선의 도착 노드가 빨강 또는 파랑이라는 뜻이다.
만약 모든 도착 노드의 색이 하나(예컨대 빨강)뿐이라면, G 자신도 빨강이어야 한다. 그러나 G가 회색인 이상, 적어도 하나의 파랑 노드로도 가야 한다. 따라서 다음과 같은 모양을 갖는다(여기에 그려지지 않은 다른 비회색 노드들도 있을 수 있다):
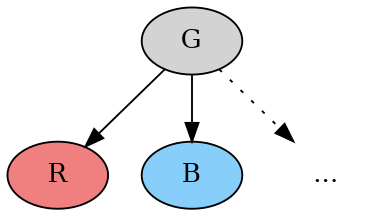
G에서 R로 가는 전이와, G에서 B로 가는 전이를 생각해 보자.
모든 상태 전이는 하나의 메시지 전달로 이루어진다(각각 M r, M b). 가능한 경우는 둘이다.
우선 경우 1이라 하자. 두 메시지는 서로 다른 컴퓨터로 가므로, 각 메시지가 영향을 미치는 전체 상태가 서로 겹치지 않는다. 따라서 두 메시지를 둘 다 전달하는 연산은 교환 가능하다. 즉, M r를 M b보다 먼저 전달하든, M b를 M r보다 먼저 전달하든, 수신한 컴퓨터의 내부 상태는 동일하게 변하며, 그 컴퓨터가 내보내는 새 메시지들의 집합도 동일하다(M b에 대해서도 마찬가지). 그러므로 이 둘은 교환해야 한다.
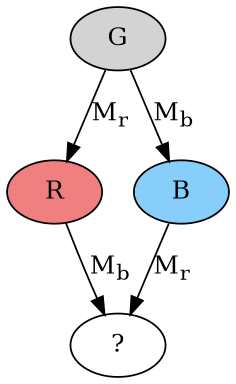
그러나 이는 모순이다. 물음표("?")로 표시된 노드는 동시에 빨강이면서 파랑일 수 없기 때문이다.
이제 경우 2를 보자. 두 메시지가 같은 컴퓨터 C에 전달되는 경우다. 합의 프로토콜이 결함 허용이라면, C가 크래시하여 메시지 처리를 멈추더라도 시스템이 복구하여 진행할 수 있는 방법이 반드시 있어야 한다3.
C가 크래시하더라도 시스템이 복구할 수 있는 방법이 있다면, 최소한 하나의 메시지가 — 이미 전송되어 있고, C가 아닌 다른 컴퓨터로 향하는 — 존재해야 하며, 그 메시지를 전달하면 복구가 일어나야 한다(즉, C 없는 시스템이 결정을 내리게 하는 경로가 있어야 한다).
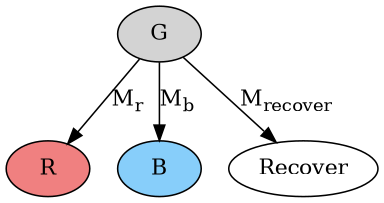
복구 노드는 무슨 색일까? 일반성을 잃지 않고 빨강이라고 하자. 그러면 앞서 본 경우 1과 똑같은 상황이 된다. M b와 M recover는 서로 다른 두 컴퓨터로 전달되므로, 어떤 순서로 전달하느냐에 따라 같은 교환성 문제가 다시 발생한다.
어느 쪽이든, G가 회색 노드로의 전이를 갖지 않는다는 최초의 가정은 모순으로 귀결된다.
비동기 모델이 매우 강한(즉, 프로토콜이 할 수 있는 일을 크게 제약하는) 가정이라는 점은 짚고 넘어갈 가치가 있다. 모델을 바꾸면 프로토콜이 이 문제를 회피할 수 있다. 예를 들어 Michael Ben-Or의 Another Advantage of Free Choice: Completely Asynchronous Agreement Protocols는 확률 1(거의 확실히)로 합의에 도달하는 합의 프로토콜을 제시한다.
또한 실제 시스템에는 보통 어떤 형태로든 시계가 존재하며, 안전성(safety)을 위해 시계 드리프트 가정을 쓰지 않는 프로토콜이라도 진행성(liveness)에서는 그 가정에 의존할 수 있다. 최소한의 가정하에서는 진행성을 형식적으로 보장할 수 없다는 사실을 아는 것이 유익하지만, 여전히 이것을 공학적 문제로 보고, 현실에서는 거의 항상 잘 작동하는 해법들로 다룰 수 있다.
실제로 위에서 묘사한 시나리오는 일종의 라이브락으로 나타나곤 한다. 예컨대 두 리더가 서로 상대가 죽었다고 오해해 리더 선출이 반복되는 식이다. 이는 합의 시스템에서 실제로 중요한 문제이며 다룰 가치가 있지만, 네트워크가 적대적으로 행동하는 경우는 드물고, 실무에서는 대개 큰 어려움 없이 해결할 수 있다.
(위의 경우 2에 대한 논증은 논문에 제시된 것과 조금 다르다. 여전히 올바르다고 생각하지만, 물론 오류가 있다면 전적으로 내 책임이다.)
분산 합의가 무엇이며 전형적인 프로토콜이 어떻게 동작하는지 개요는 Distributed Consensus를 보라.↩︎
진정한 비동기 결정적 분산 시스템에 대해 이 모델이 타당하다는 건 어렵지 않게 납득할 수 있지만, (복구 메시지와 사실상 동시에 원래 메시지도 보내야 한다는) 이 사실은 꽤 놀랍다고 생각한다! 내게는, 모델의 동작을 정확히 못 박는 일이 증명의 큰 부분을 차지한다.↩︎
실제로 결함이 발생하기를 요구하는 건 아니다! 단지 결함이 발생했을 때 프로토콜이 복구할 수 있어야 한다.↩︎