재생에너지 시스템 전공자가 MATLAB과 Java를 거쳐 하스켈로 분산 전력 제어 소프트웨어를 개발하게 된 여정을 바탕으로, 단위 안전성과 타입 주도 개발, 속성 기반 테스트가 왜 재생에너지 기술의 복잡성을 다루는 데 특히 효과적인지 설명한다.
내 배경은 소프트웨어 엔지니어가 되는 전형적인 경로와는 다릅니다. 저는 컴퓨터 과학을 전공하지 않았습니다. 대신 HTW 베를린에서 재생에너지 시스템 전공으로 학사와 석사를 모두 취득했습니다. 그러다 보니 어쩌다 보니 하스켈을 전문으로 하는 개발자가 되어, 분산 전력 관리 및 공급 시스템을 구축하고 있습니다.
유럽의 기술 구직 시장은 주로 Java와 C# 같은 객체지향 언어가 지배합니다. 반면 하스켈은 상대적으로 틈새 언어로, 흔히 블록체인이나 금융과 연관되어 있죠. 하지만 제 경험으로는, 하스켈은 재생에너지 기술의 복잡성을 다루기에 완벽하게 맞는 언어이며, 함수형 프로그래밍의 장점을 크게 누릴 수 있는 분야라고 믿습니다.
이 글에서는 제가 하스켈로 들어오게 된 여정을 소개하고, 메인스트림 구직 시장에서는 존재감이 크지 않음에도 불구하고 하스켈이 재생에너지 분야에서 얼마나 큰 잠재력을 지니고 있는지 설명해 보겠습니다.
대학 시절, 열역학과 에너지 공정 공학은 학생들 사이에서 악명이 높았습니다. 공식은 끝도 없이 많았고, 시험장에서 참고하기에는 너무 복잡했죠.
하지만 교수님의 한 가지 조언이 제 관점을 바꿨습니다. 국제단위계(SI)를 제대로 이해하라고 하시면서, 특히 7개의 기본 단위1로 단위를 조합하고 분해하는 연습을 강조하셨습니다.
예를 들어, 와트(전력)는 기본 단위인 킬로그램, 미터, 초로 분해할 수 있습니다(W = kg · m² / s³). 이 요령을 터득하고 나서, 저는 외우는 대신 단위가 저를 안내하도록 문제를 풀 수 있었습니다. 적어야 할 것을 최소화했고, 시험을 넉넉히 끝내면서 매번 만점을 받을 수 있었죠.
그때는 몰랐지만, 이렇게 구조와 단위에 사고를 맡기는 사고방식이 훗날 알게 된 개념인 타입 주도 개발(type-driven development)과 놀랍도록 닮아 있었습니다.
학업 초기에 저는 학교 연구실 중 한 곳에서 파트타임으로 일하기 시작했습니다. 첫날 MATLAB 책을 건네받았고, 일주일간 독학한 뒤 태양광 저장 시스템을 위한 시뮬레이션 모델과 제어 알고리즘 개발에 기여하기 시작했습니다.
이런 모델과 알고리즘은 재생에너지 시스템에서 특히 중요합니다. 전통적인 화석 연료 발전원은 반응이 느리고 비교적 예측 가능한 정상 상태로 동작하는 경향이 있지만, 재생에너지는 본질적으로 변동성이 큽니다. 재생에너지는 유연성과 지능형 제어가 뒷받침될 때 비로소 빛을 발합니다.
그때 우리가 작성한 코드는 결코 아름답지 않았습니다. 예를 들어, 다음은 우리가 공개했던 AC 결합 리튬이온 배터리를 시뮬레이션하는 함수입니다:
function [Ppv, Pbat, Ppvs, Pbs, Pperi, soc] = PerModAC(s, sim, pvmod, Pl, ppv)
SOC_h = s.SOC_h; % 배터리 재충전에 대한 히스테리시스 임계값
P_AC2BAT_DEV = s.P_AC2BAT_DEV; % 충전 전력의 평균 정상 편차(W)
P_BAT2AC_DEV = s.P_BAT2AC_DEV; % 방전 전력의 평균 정상 편차(W)
% ...
자세한 내용은 생략하겠지만, Python이나 MATLAB 같은 스크립트 언어의 주요 문제가 금세 드러납니다:
이 예제에서 인자 ppv는 PV 발전기의 정규화된 DC 출력이 kW/kWp2 단위를 갖는 벡터여야 합니다.
하지만 이 함수의 호출자가 무엇이든 전달하는 것을 막을 방법이 없습니다. 심지어 문자열을 넘길 수도 있죠. 게다가, 이런 말 해도 될지 모르겠지만, 저는 단위 테스트가 무엇인지 아는 MATLAB 프로그래머를 거의 보지 못했습니다. 우리가 하던 테스트 방식은 그래프를 생성해 측정 데이터와 정성적으로 비교하는 것이었습니다. 이 과정은 시간도 오래 걸리고 오류도 쉽게 발생합니다. 자주 실행하고 충분히 검증할 때만 효과적이며, 자동화 도구의 도움을 받기보다 사람의 노력을 크게 의존합니다. 제대로 된 안전장치가 없으면 작은 오류가 쉽게 눈에 띄지 않은 채 넘어가서, 코드는 취약해지고 디버깅은 더 어려워집니다.
제 첫 정규직은 Java로 섹터 커플링 재생에너지 시스템을 위한 시뮬레이션 소프트웨어를 작성하는 일이었습니다. 컴파일러가 타입 안전성을 어느 정도 제공해 준다는 사실만으로도 이전의 MATLAB 경험에 비해 큰 진전이었죠. 예를 들어, 배터리 시뮬레이션 모델은 대략 다음과 같을 수 있습니다3:
public class ACBattery {
ACBatterySpec spec;
// 에너지 함량(Wh)
double energyWh;
// 생성자는 간결성을 위해 생략
/**
* @param powerW - 충전 전력(와트)
* @param durationS - 지속 시간(초)
*/
public void charge(double powerW, double durationS) {
// 간결성을 위해 구현 생략
}
}
호출자가 완전히 엉뚱한 타입을 넘기는 일은 막을 수 있게 되었지만, 여전히 두 가지 큰 문제가 남아 있습니다:
charge 함수의 두 인자는 의미론적으로 다르지만 타입은 같습니다.세 번째 문제는 객체지향 언어가 상태 지향으로 설계되어 있다는 점입니다. 이는 동시성을 어렵게 만들고, 테스트도 매우 까다롭게 합니다.
이 접근은 누군가 잘못된 단위를 가진 값을 넘기거나, 구현에서 인자를 잘못 사용하는 일을 막기에 충분히 표현력이 높지 않습니다. 결국 타입 안전성의 부족을 메우기 위해 단위 테스트를 작성해야 합니다.
기술적으로는 각 인자에 대해 타입을 정의할 수 있습니다. 예를 들어, 단위를 인코딩하기 위해 unit-api 라이브러리를 사용할 수 있습니다:
public class ACBattery {
ACBatterySpec spec;
Quantity<Energy> energy;
// 생성자는 간결성을 위해 생략
/**
* @param power 충전 전력
* @param duration 충전 시간
*/
public void charge(Quantity<Power> power,
Quantity<Time> duration) {
Quantity<Energy> energyAdded =
power.multiply(duration).asType(Energy.class);
this.energy = this.energy.add(energyAdded);
}
}
이 접근은 훨씬 견고합니다:
하지만 Java 같은 언어에서는 대가가 따릅니다:
+, -, *, …) 대신 재정의된 함수(add, multiply 등)를 사용해야 합니다.유지해야 하는 상용구 코드(보일러플레이트)도 크게 늘어납니다. 이는 비즈니스가 가장 중요하게 여기는 것, 즉 "개발자 생산성"을 해칩니다.
제가 여러 Java 코드베이스에서 일한 경험으로는, 결국 모두가 물리량을 원시 타입으로 다루는 쪽으로 귀결되어, 안전성을 단순함과 속도에 맞바꾸게 되었습니다.
이미 단위가 사고를 이끌도록 했을 때의 이점을 맛본 터라, 타입 시스템이 동일한 신뢰성을 제공할 수 있는지 자연스럽게 탐구하게 됐습니다. 약 5년 전 저는 독학으로 하스켈을 배우기 시작했고, 1년 뒤 현재의 직장에서 재생에너지 분야에 제가 열정을 쏟아온 하스켈을 실무에 사용할 기회를 얻게 되었습니다.
하스켈에서 타입은 현실 세계의 제약을 코드에 직접 표현하는 엄격한 틀입니다. 다음은 하스켈의 dimensional 라이브러리를 사용해 같은 charge 함수의 타입 시그니처를 표현한 예입니다. 이 라이브러리는 "7개의 SI 기본 차원"을 사용해 물리량에 대해 정적으로 검사되는 차원 연산을 제공합니다:
data ACBattery num
= ACBattery
{ spec :: ACBatterySpec
, energy :: Energy num
}
charge :: Fractional num => Power num -> Time num -> ACBattery num -> ACBattery num
charge power time battery = -- 간결성을 위해 구현 생략
함수형 언어가 익숙하지 않다면 다소 난해해 보일 수 있지만, 차근차근 살펴보겠습니다:
Fractional num이라는 타입 제약을 사용합니다. 호출자는 기저 숫자 표현을 지정할 수 있다는 뜻입니다. 예컨대 num은 부동소수점 Double일 수도 있고, 더 정밀한 fixed-point 표현인 Pico나 Milli일 수도 있습니다.덜 일반화한 버전은 이렇게 생겼을 겁니다:
charge :: Power Double -> Time Double -> ACBattery Double -> ACBattery Double
charge power time battery = -- 간결성을 위해 구현 생략
첫 번째와 두 번째 인자는 배터리에 공급하는 전력과 그 전력을 공급하는 시간입니다.
세 번째 인자인 ACBattery는 배터리의 현재 상태입니다. 하스켈은 기본적으로 상태를 변경하지 않기 때문에, (불변) 상태를 입력으로 받아 새로운 상태를 반환합니다. 이는 코드에 대한 추론과 테스트를 훨씬 단순하게 만듭니다.
마지막의 -> ACBattery num은 함수가 충전 이후 업데이트된 배터리 상태로 평가된다는 뜻입니다.
여기에는 위험한 수동 단위 변환도, 변수 이름에 단위를 적어 넣는 일도 없습니다. 이는 파싱하고, 검증하지 말라(Parse, don’t validate) 원칙과도 완벽히 맞아떨어집니다. 기대하는 바를 타입에 인코딩함으로써, 올바르게 구성된 데이터만 핵심 로직으로 들어오게 보장할 수 있습니다. 데이터가 이런 타입으로 파싱되고 나면 런타임에 다시 확인할 필요가 없습니다. 컴파일러가 이미 보증해 줍니다.
함수를 더 단순화해 에너지 변환만 보겠습니다:
charge :: Power Double -> Time Double -> Energy Double -> Energy Double
charge power time energy =
energy + power * time
배터리의 상태 대신, 이 버전은 충전 전 배터리의 에너지를 받아 충전 후의 에너지로 평가됩니다.
단위 라이브러리를 사용하는 데 장황한 메서드 호출(add, multiply 등)이 필요한 Java와 달리, 여기서는 익숙한 산술 연산자를 그대로 사용할 수 있습니다. 또 다른 장점은 dimensional이 하스켈의 newtype 선언을 사용하기 때문에, 각 물리량이 내부적으로는 해당 기저 숫자 타입 그대로 표현된다는 점입니다. 즉, 런타임에서 순수 숫자 연산과 비교해 무시할 만한 오버헤드4만 발생한다고 기대할 수 있습니다. 객체 할당과 동적 디스패치에 의존하는 Java의 단위 라이브러리와는 다릅니다.
charge 함수를 호출할 때는 단위를 직접 지정합니다:
example = charge chargingPower duration currentEnergy
where
chargingPower = 1 *~ kilo Watt
duration = 30 *~ second
dimensional 라이브러리는 호환 가능한 물리량만 조합하도록 보장합니다. 인자의 순서를 실수로 바꾸거나 잘못된 연산을 사용하면, 런타임에 불가사의한 버그를 만나는 대신 즉각적이고 명확한 타입 오류를 받게 됩니다:
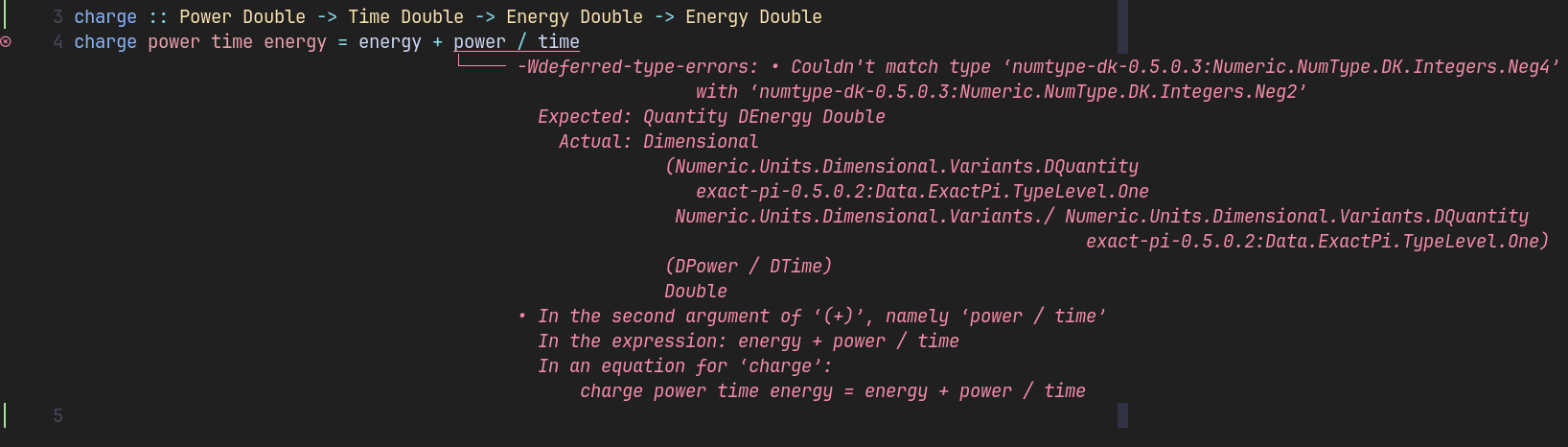
power * time으로 곱하면, 나누려 할 때와 달리 오류가 사라집니다. 단위가 맞기 때문이죠. 거의 마법처럼 느껴집니다. 하스켈의 타입 시스템과 dimensional을 함께 사용하면, 컴파일러가 올바른 구현으로 당신을 이끌어 줍니다. 단위 안전성, 도메인 모델링, 강한 타입은 학문적 장난이 아닙니다. 재생에너지를 포함한 다양한 분야에서 신뢰할 수 있고 유지보수하기 쉬운 소프트웨어를 만드는 실용적인 도구입니다.
그동안 저는 몰랐습니다. 내 열역학 교수님은 이미 하스켈이 재생에너지 기술에 완벽히 어울린다는 사실을 가르쳐 주고 계셨던 셈이죠!
저는 테스트 주도 개발(만들 때까지 가짜로)을 강력히 지지합니다. 제 경험상, 높은 품질의 의미 있는 테스트 커버리지를 보장하는 가장 좋은 방법입니다. 사람들이 TDD를 꺼리는 주된 이유 중 하나는, 특히 전통적 OOP에서는 타입 안전성이 약한 부분을 단위 테스트가 메워야 해서 지루하게 느껴지기 때문입니다. 하스켈에서는 속성과 행위, 즉 중요한 것에 집중함으로써 훨씬 적은 코드로 더 많은 버그를 잡는 테스트를 작성할 수 있습니다.
QuickCheck 같은 강력한 라이브러리와 tasty-quickcheck 같은 프레임워크와의 통합을 통해, 특정 케이스나 엣지 조건을 일일이 테스트하는 대신 수학적 속성 자체를 표현하고 검증할 수 있습니다.
가상의 예시는 다음과 같습니다:
chargingTest :: TestTree
chargingTest = testGroup "Charging"
[ testProperty "최대 용량을 초과하지 않는다"
\(Positive duration) (Positive power) (Small energyDelta) ->
let previousState =
testBattery { energy = maxCapacity testBatterySpec - abs energyDelta }
newState = charge power duration previousState
newEnergy = energy newState
in newEnergy <= maxCapacity testBatterySpec
, testProperty "정격 AC 충전 전력을 초과하지 않는다"
\(Positive duration) (NonNegative deltaPower) (NonNegative energy) ->
-- 간결성을 위해 구현 생략
-- ...
]
속성 기반 테스트에서는 프레임워크가 다양한 (의사)난수 입력을 자동으로 생성해 주므로, 엣지 케이스를 손수 만들어 넣을 필요가 없습니다. 이 접근은 소수의 예시만 확인하는 대신, 코드가 도메인의 핵심 불변식과 물리 법칙을 지키는지를 검증하게 해 줍니다.
여가 시간에 하스켈 클린테크를 함께 해킹해 온 Alex Drake에게 교정해 준 데 감사드립니다.